下記の記事の続きです。
共通鍵暗号
上記の記事でも示しましたが、共通鍵暗号方式では鍵を共有する必要があり、不特定多数の相手と通信を行う時に鍵をどうやって渡すかが問題となっています(鍵配送問題)。
公開鍵暗号方式ではこの鍵配送問題を解決することができるので、この記事で説明していこうと思います。
公開鍵暗号とは
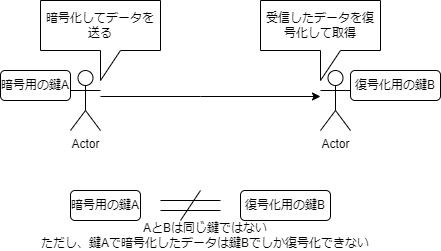
暗号化用の鍵と、復号化用の鍵の二つの鍵を使って暗号通信を実現します。
この時、暗号化用の鍵と復号化用の鍵は、1対1で対応してペアになっています。
例えば、公開鍵暗号用の暗号化用の鍵Aと復号化用の鍵Bのペアを作成すると、鍵Aで暗号化したデータは鍵Bでしか復号化できません。
この性質を使って、共通鍵暗号で使用する共通鍵の配送を行います。
公開鍵暗号を使った共通鍵の配送
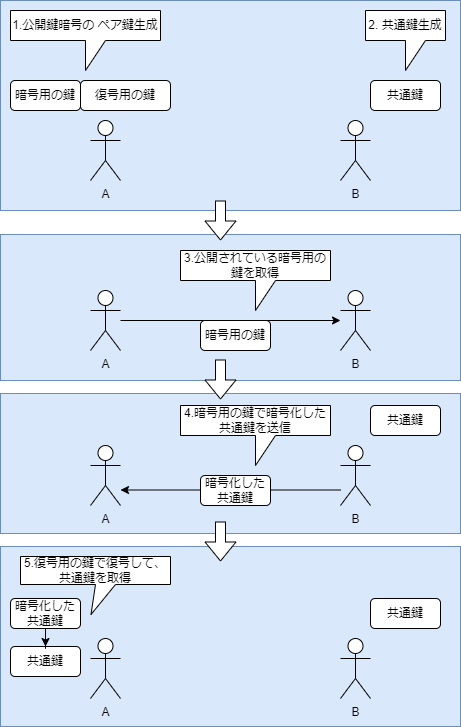
共通鍵暗号の共通鍵の配送は、下記の手順で行います。
- 公開鍵暗号の暗号化用の鍵を公開しておく(公開鍵にする)
- 公開されている暗号化用の鍵で、共通鍵を暗号化して送る
もう少し具体的にすると、下記の図のようなイメージです。
暗号化用の鍵とペアになっている復号化用の鍵を誰にも渡さない状態(プライベート鍵)にしておけば、
共通鍵を入手できるのは、復号化用の鍵を持っている人間だけになります。
このように共通鍵を通信したい相手のみと共有します。
ハイブリッド暗号システム
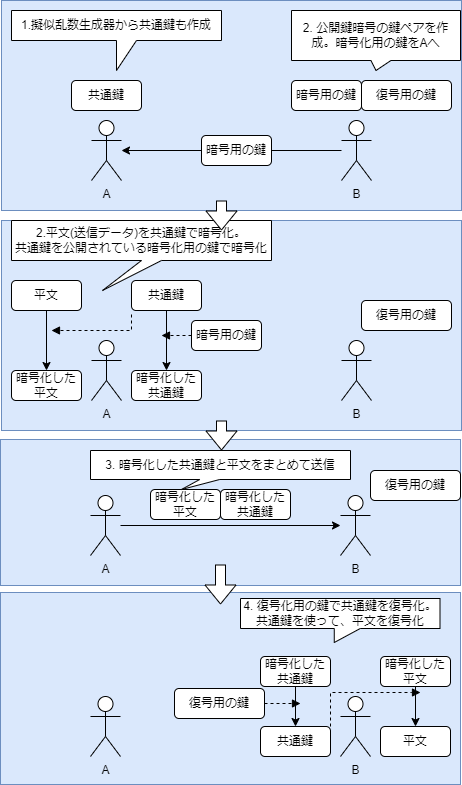
上記で示した、公開鍵暗号で共通鍵を共有し、暗号化通信を行うシステムのことを、ハイブリッド暗号システムと呼ばれることがあります。
実際の共通鍵生成から、鍵交換、暗号化通信までの流れは下記のようになります。
共通鍵は通信の度に生成するしくみとなります(ここで使用する共通鍵をセッション鍵と呼びます)。
全ての通信を公開鍵暗号でやればよいのではと思う方もいらっしゃるかと思いますが、公開鍵暗号は共通鍵暗号より通信速度が遅いという性質があるため、このような方法を取っています。
セッション鍵(共通鍵)は通信の度に変わりますが、公開鍵は通信の度に必ず変わるわけではないので、公開鍵のビット長は長めに設定するのが良いとされています。もちろんセッション鍵も短くて良いというわけではありません。セッション鍵を必要以上に短くすると、ブルートフォースアタックにより破られる可能性もあります。
公開鍵暗号の代表的な方式
ここからは公開鍵暗号方式の代表的なものの概要を示します。計算式などは割愛しています(時間があればそれも記事にしたいですが。。。)
RSA
大きな数の素因数分解を高速で解く方法が現状ないことを利用した暗号方式です。
よく使われるものなので、暗号化と復号化、鍵ペアの作成に関して簡単に説明します。
RSAの暗号化
次の式で成り立つように暗号化します。
暗号文 = (平文のE乗) mod N
平文をE乗して、Nで割った時の余りを暗号文とします。このEとNのペアが公開鍵となります(公開鍵は(E,N)と表現します)。
RSAの復号化
次の式で成り立つように復号化します。
平文(復号後) = (暗号文のD乗) mod N
平文をD乗して、Nで割った時の余りを暗号文とします。Nは暗号化の時に使用したものと同値です。このDとNがプライベート鍵となります(プライベート鍵は(D,N)と表現します)。
鍵ペアの作成方法
下記の手順で作成します。
- Nを求める
- 擬似乱数生成器で桁数が大きい素数二つの値p,qを用意し、p×qをNとする
- L(p-1,q-1の最小公倍数)を求める
- Eを求める
- 1<E<Lとなり、EとLの最大公約数が1となる。これと擬似乱数生成器を使って計算する
- Dを求める
- 1<D<L、E×D mod L = 1を満たすDを計算する
E,D,Nが大きな値であればあるほど、ブルートフォースアタックによる攻撃は困難になります。
RSA-OAEP
任意の暗号文を復号化させることによる攻撃(選択暗号文攻撃)への対処のために使用されます。間違った暗号文に対して「ここが間違っている」というレスポンスを期待して行う攻撃に対処するためのものです。
RSA-OAEPは暗号文に認証情報を追加し、これが間違っている場合は一律で「認証エラー」を返し、具体的なエラー内容を返さないことで前述の攻撃の対処を行います。
ElGamal方式
(平文) mod Nで離散対数を求めるのが困難なことを利用した公開鍵暗号方式です。鍵の長さが平文の二倍になります。
Rabin方式
(平文) mod Nで平方根を求めるのが困難なことを利用した公開鍵暗号方式です。
楕円曲線暗号(ECC)
楕円曲線と呼ばれる曲線を定めて、その曲線の上に乗っている点に対して特殊な乗算によって暗号化します。RSAに比べて鍵のビット数を少なくできるため、利用されることも多いです。
公開鍵暗号で防げないこと
man in the middle攻撃(攻撃者が通信の間に入り、仲介することによる攻撃)を防ぐことはできません。これに対処するためには公開鍵の証明書が必要になります。証明書に関しては別の記事で説明しようかと思います。
参考文献
- 暗号技術入門 秘密の国のアリス(書籍)
https://cr.hyuki.net/