まえがき
ソーシャルゲームにおいてどれだけの確率で当たりを引くか(当選確率)は、課金や、高レアのキャラクターやアイテムが当たるまでリセットし続けるリセットマラソン(リセマラ)を行う基準となるので重要である。これまで、多くのインターネット上の記事では、試行回数・出現確率が決まっている時の当選確率が議論されてきた。しかし、試行回数や出現確率を変化させた時の当選確率は、ほとんど議論されていない。そこで本稿では、出現確率($P_s$)、試行回数(N[回])と当選確率の関係を明らかにする。
当選確率の導出
出現確率$P_s$、試行回数N[回]までにおける当選確率は、確率の余事象を用いて以下のように求められる。
\begin{split}
当選確率 &= 1-すべて外れる確率\\
&= 1-(出現しない確率)^N\\
&= 1-(1-P_s)^N
\end{split}
当然、以下のように二項分布を用いて直接求めることもできる。
\begin{split}
当選確率 &= \sum_{k=0}^{N-1} {}_N \mathrm{C}_k (1-P_s)^k(P_s)^{N-k}
\end{split}
しかし、計算回数がより少ない方が計算時間が短く済むので、余事象を用いる方法を採用する。
性能評価
縦軸:当選確率・横軸:試行回数(当選確率 vs 試行回数(N))のグラフ、縦軸:当選確率・横軸:出現確率(当選確率 vs 出現確率($P_s$))のグラフを描画することで性能評価を行う。本稿では、試行回数が増加しても$P_s$は変化しないものとする。
なお、グラフ描画と計算がまとめてできるためExcelを用いて計算を行った。
性能評価諸元
ソーシャルゲームにおける最高ランクアイテムの$P_s$は、概ね0.005~0.03(=0.5%~3%)である。さらに、一般に$P_s$=0.01、N=100の時、当選確率は、約0.63(=63%)であることが知られている。
そこで今回、用いる性能評価諸元は以下のようにする。
ガチャ1回当たりの値段:300円
当選確率 vs 試行回数(N)のグラフ
$P_s$:0.005, 0.01, 0.03
$N$:0, 1, ..., 199, 200
当選確率 vs 出現確率($P_s$)のグラフ
$P_s$:0, 0.001, ..., 0.045
$N$:100, 200, ..., 600
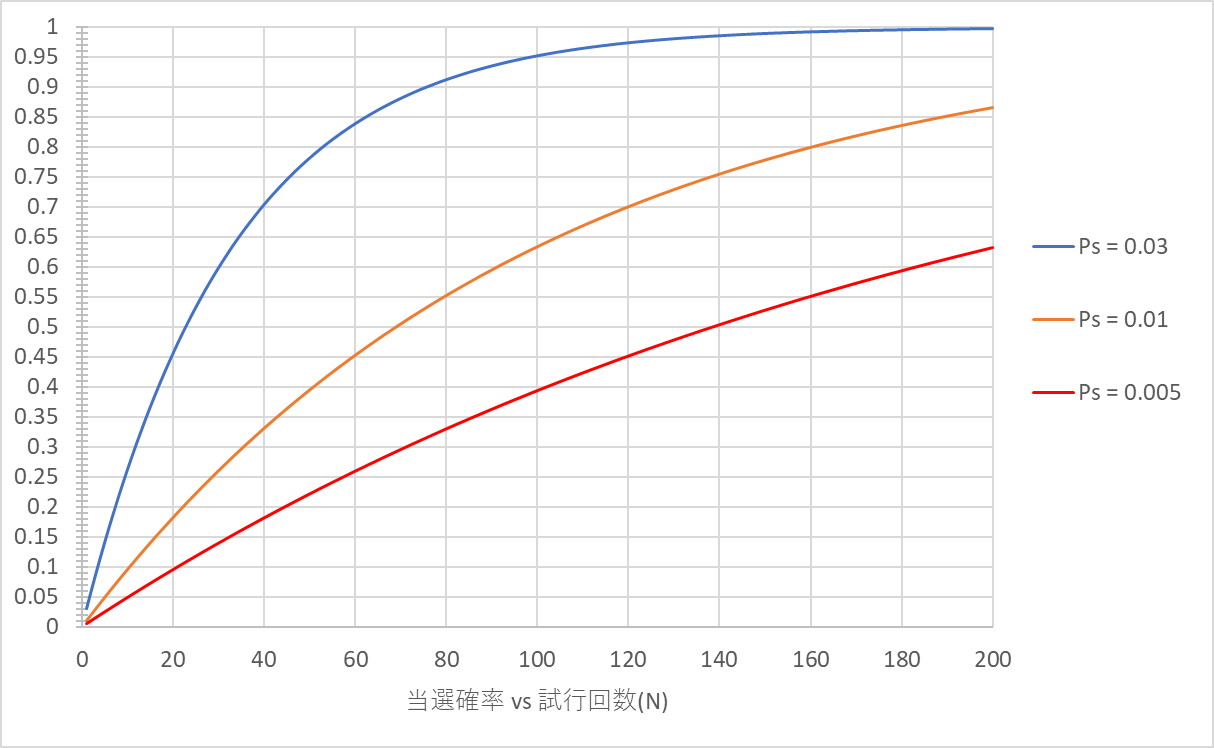
当選確率 vs 試行回数(N)のグラフ
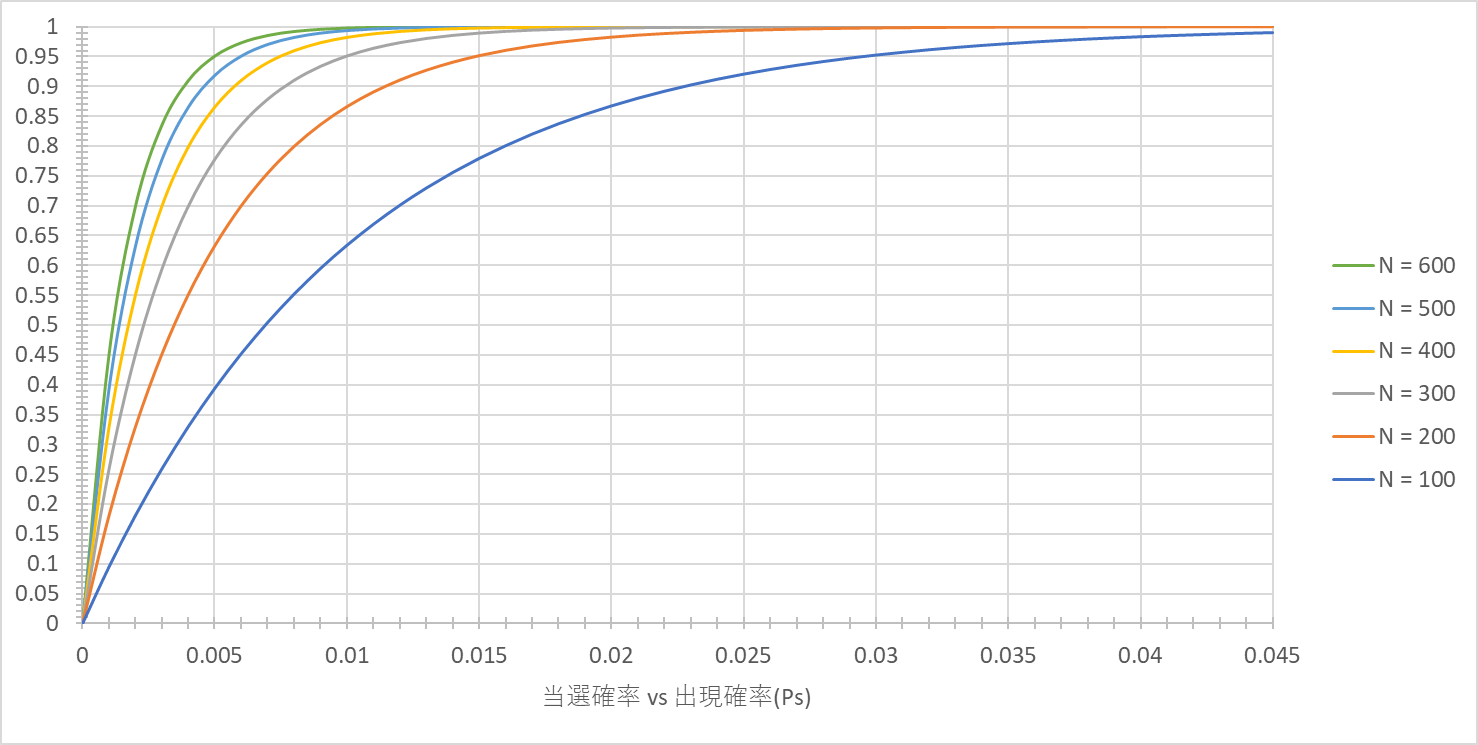
当選確率 vs 出現確率(Ps)のグラフ
当選確率 vs 出現確率(Ps)のグラフは以下のようになる。
考察
当選確率 vs 試行回数(N)のグラフからN>140の時、全ての$P_s$で当選確率>0.5を達成している。
さらに、$P_s$=0.03の時、N=170で当選確率=1を達成できることが分かる。ここから、$P_s\geqq 0.005$の場合、42000円以上課金すれば50%以上の確率で最高ランクのアイテムが入手できることが分かる。
また、当選確率 vs 出現確率(Ps)のグラフから$P_s$=0.005の時、N$\geqq$300の時、当選確率$\geqq$0.75を達成する。ここから、90000円課金することで75%以上の確率で最高ランクアイテムが入手できる。
さらに、$P_s$を固定した時、Nの増加量に対する当選確率の増加量は、Nが大きくなるにしたがって小さくなる(ex. $P_S$=0.01の時、N=100からN=200に増加した時の当選確率は約23ポイント増大しているが、N=200からN=300に増加した時の当選確率は約10ポイントしか増加しない。)
ここから、出現確率が常に一定のガチャの場合、課金すればするほど割に合わないといえる。
さらに、$P_s\geqq$0.024の時、N$\geqq$100で当選確率=0.9を達成する。
ここから、$P_s\geqq$0.024の時、30000円課金することで90%以上の確率で最高ランクのアイテムが入手できる。
まとめ
本項では、出現確率($P_s$)、試行回数(N[回])と当選確率の関係を明らかにした。ここから
$P_s\geqq 0.005$の場合、42000円(300円/回)以上課金すれば50%以上の確率で最高ランクのアイテムが入手できることを明らかにした。さらに、出現確率が常に一定のガチャの場合、課金すればするほど当選確率の伸びが悪くなり、割に合わなくなることも明らかにした。
最後に
本稿はソーシャルゲームで課金しているユーザを非難しているものではありません。あくまでも、計算したらこうなるということを示し、その結果を基に考察したものです。