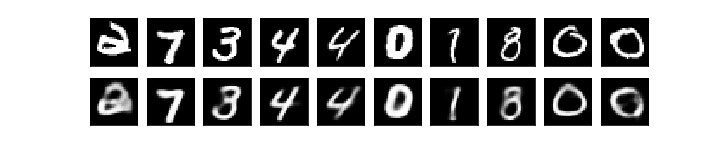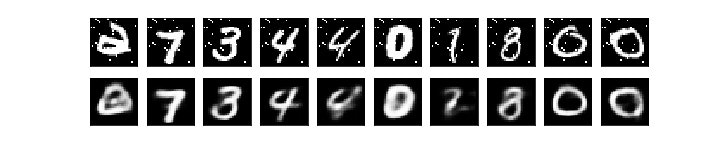はじめに
今回諸事情でqiitaに記事を書くことになったので、前々から気になっていた変分オートエンコーダについて解説していこうと思います。
今回の記事では理論的な部分も記載しておりますが、あくまで「ふわっと解説」であり、自分の解釈なども含まれているため、他のサイトと比較しながら見ることをお勧めします。
また、不正確な部分や誤った記述をしている部分に関しては、ご指摘いただけると幸いです。
AE(オートエンコーダ)とは
VAEについて解説する前に、ベースとなるAEについての解説を行いたいと思います。
AEとは、機械学習における教師無し学習の手法の一つであり、入力データに対してそれと一致するデータを出力する手法です。
具体的な構造は、下記のようになります。
図を見るとわかる通り、AEは2つのニューラルネットワークを用いた手法となっています。
正確には、入力データをそれよりも低次元のデータである潜在変数$Z$に圧縮するエンコーダと、圧縮したデータを元の次元の特徴に変換するデコーダの2つで構成されています。
このような構造により、AE自体は入力データに対するノイズ除去の役割もありますが、エンコーダとデコーダを個々で用いることで、エンコーダは入力データを次元削減する特徴抽出モデル、デコーダは潜在変数Zからデータを生成するモデルと考えることもできます。
VAE(変分オートエンコーダ)とは
結論からいいますと、VAEはAEでのエンコーダから得た潜在変数$Z$に対して確率分布を仮定した場合の手法になります。
具体的な構造は、下記のようになります。
先ほどの図と見比べるとわかるように、確率分布からサンプリングして得たZを用いている点が異なります。
VAEでは平均0, 分散1の標準正規分布$N(0, 1)$を$Z$の分布として仮定しています。そして、エンコーダで出力した平均と分散をもとに作られた確率分布から、潜在変数$Z$をサンプリングにより取り出し、デコーダではその復元を行います。
ただし、実際にデータを用いて行う場合は、学習によって得られた標準正規分布に近い平均$μ$, 分散$Σ$の多変量ガウス分布$N(\mu, \Sigma)$からサンプリングを行います。
上記のようにVAEはニューラルネットワークを用いたAEとほとんど違いがないことがわかります。しかしVAEでは、潜在変数Zに対して標準正規分布に従うという制約を設けています。そのため、あるZと似た値が入力された場合でも、デコーダでは似たようなデータを出力することができます。
周辺対数尤度関数の最適化
VAEはオートエンコーダであるため、これに対する最適化である周辺対数尤度関数$\ln p_{\theta}(X)$の最大化を行うことで、パラメータを推定します。
ここで、パラメータと関数は以下のようになります。
$θ$:デコーダ内のパラメータ
$φ$:エンコーダ内のパラメータ
$Z$:潜在変数
$p_{\theta}(X)$:周辺尤度関数
$p(Z)$:事前分布
$p_{\theta}(Z|X)$:真の事後分布
$q_{\phi}(Z|X)$:近似事後分布
この時、周辺対数尤度関数は以下のように式変形できます。
\begin{align}
\ln p_{\theta}(X) &= \ln \int p_{\theta}(X, Z)dz\\
&= \ln \int q_{\phi}(Z|X)\frac{p_{\theta}(X, Z)}{q_{\phi}(Z|X)}dz\\
\end{align}
式の展開により、対数の中で積分を行っていますが、これに対する計算は一般に困難とされています。そのため、イェンセンの不等式を用いて$\ln p_{\theta}(X)$の変分下限$L[q_{\phi}(Z|X)]$を求め、この値を大きくすることで$\ln p_{\theta}(X)$の最大化を考えます。
先ほどの式に、イェンセンの不等式を適用した場合の式変形は以下のようになります。
\begin{align}
\ln p_{\theta}(X) &= \ln \int q_{\phi}(Z|X)\frac{p_{\theta}(X, Z)}{q_{\phi}(Z|X)}dz\\
&\geqq \int q_{\phi}(Z|X) \ln \frac{p_{\theta}(X, Z)}{q_{\phi}(Z|X)}dz\\
=& L[q_{\phi}(Z|X)]
\end{align}
次に、$\ln p_{\theta}(X)$と$L[q_{\phi}(Z|X)]$の差を求めます。式は以下のようになります。
\begin{align}
\ln p_{\theta}(X) - L[q_{\phi}(Z|X)] &= \ln p_{\theta}(X) - \int q_{\phi}(Z|X) \ln \frac{p_{\theta}(X, Z)}{q_{\phi}(Z|X)}dz\\
&= \int q_{\phi}(Z|X) \ln p_{\theta}(X)dz - \int q_{\phi}(Z|X) \ln \frac{p_{\theta}(Z|X) p_{\theta}(X)}{q_{\phi}(Z|X)}dz\\
&= \int q_{\phi}(Z|X) \ln p_{\theta}(X)dz - \int q_{\phi}(Z|X)\{\ln p_{\theta}(Z|X) + \ln p_{\theta}(X) - \ln q_{\phi}(Z|X)\}dz\\
&= \int q_{\phi}(Z|X)\{\ln q_{\phi}(Z|X) - \ln p_{\theta}(Z|X)\}dz\\
&= \int q_{\phi}(Z|X) \ln \frac{q_{\phi}(Z|X)}{p_{\theta}(Z|X)}dz\\
&= KL[q_{\phi}(Z|X)||p_{\theta}(Z|X)]
\end{align}
周辺対数尤度関数とその下限の計算結果は、学習によって得た近似事後分布$q_{\phi}(Z|X)$と真の事後分布$p_{\theta}(Z|X)$のKLダイバージェンスとなります。この値は、$q_{\phi}(Z|X)$が$p_{\theta}(Z|X)$に近づくことから値が小さくなるため、$\ln p_{\theta}(X)$の最大化は、$L[q_{\phi}(Z|X)]$の最大化に置き換えることができます。
この式2を用いて、再度変分下限$L[q_{\phi}(Z|X)]$に対する式の置き換えを行います。
\begin{align}
L[q_{\phi}(Z|X)] &= \ln p_{\theta}(X) - KL[q_{\phi}(Z|X)||p_{\theta}(Z|X)]\\
&= \ln p_{\theta}(X) - \int q_{\phi}(Z|X) \ln \frac{q_{\phi}(Z|X)}{p_{\theta}(X, Z)}dz\\
&= \ln p_{\theta}(X) - E_{q_{\phi}(Z|X)}\{\ln q_{\phi}(Z|X) - \ln p_{\theta}(Z|X)\}\\
&= \ln p_{\theta}(X) - E_{q_{\phi}(Z|X)}\{\ln q_{\phi}(Z|X) - \ln p_{\theta}(X,Z) + \ln p_{\theta}(X)\}\\
&= \ln p_{\theta}(X) - E_{q_{\phi}(Z|X)}\{\ln q_{\phi}(Z|X) - \ln p_{\theta}(X|Z) - \ln p(Z) + \ln p_{\theta}(X)\}\\
&= - E_{q_{\phi}(Z|X)}\{\ln q_{\phi}(Z|X) - \ln p_{\theta}(X|Z) - \ln p(Z) \}\\
&= E_{q_{\phi}(Z|X)}\{\ln p_{\theta}(X|Z)\} - E_{q_{\phi}(Z|X)}\{\ln q_{\phi}(Z|X) - \ln p(Z) \}\\
&= E_{q_{\phi}(Z|X)}\{\ln p_{\theta}(X|Z)\} - E_{q_{\phi}(Z|X)}\{\ln \frac{q_{\phi}(Z|X)}{p(Z)}\}\\
&= E_{q_{\phi}(Z|X)}\{\ln p_{\theta}(X|Z)\} - KL[q_{\phi}(Z|X)||p(Z)]
\end{align}
$L[q_{\phi}(Z|X)]$を変換した後の式は、上記2つの項から成り立つ式が得られます。ここで、エンコーダはデータ$X$を得た時の近似事後分布$q_{\phi}(Z|X)$で、デコーダは$Z$を得た時の$X$の事後分布$p_{\theta}(Z|X)$となります。
そのため、第一項で事後分布に対数をとった値に期待値をとったものは、入力データ$X$と出力データ$\hat{X}$がどれだけ似ているかを表す関数と考えることができ、再構成誤差と呼ばれています。
また、第二項は$q_{\phi}(Z|X)$と$p(Z)$のKLダイバージェンスであり、この項を小さくすることは$q_{\phi}(Z|X)$を自身で設定した事前分布$p(Z)$に近づけることと等価になります。そのため、この項は正規化項となります。
損失関数
それぞれの確率分布は以下を仮定しています。
・$p(Z)$ ~ $N(0, I)$
・$q_{\phi}(Z|X)$ ~ $N(\mu, \Sigma)$
まず、第一項に着目してゆきます。今回実験で使用するのは白黒の画像データであり2値変数の入力を仮定できます。そのため、$p_{\theta}(Z|X)$はベルヌーイ分布を仮定することができるため、入力データの次元数をDとすると、以下のような式であるといえます。
\begin{align}
p_{\theta}(X|Z) &= \prod_{d=1}^{D} (y_{d})^{x_{d}} (1-y_{d})^{1-x_{d}}
\end{align}
この時、モンテカルロ積分を用いることで、第一項の式はバイナリクロスエントロピー誤差として導出することができるため、式は以下のようになります。
\begin{align}
E_{q_{\phi}(Z|X)}\{\ln p_{\theta}(X|Z)\} = \sum_{d=1}^{D}\{x_{d} \ln y_{d} + (1 - x_{d}) \ln (1 - y_{d})\}
\end{align}
第二項は、多変量正規分布$q_{\phi}(Z|X)$と$p(Z)$のKLダイバージェンスとなります。
この時、先ほど求めた$q_{\phi}(Z|X)$と$p_{\theta}(Z|X)$のKLダイバージェンスを例に考えると、$KL[q_{\phi}(Z|X)||p_{\theta}(Z|X)]$は、対数とった値に対して$q_{\phi}(Z|X)$の期待値をとったものとみなすことができます。そのため、今回のKLダイバージェンスに対しても、同じように考えた場合は以下のように式変形できます。
\begin{align}
\int q_{\phi}(Z|X) \ln \frac{q_{\phi}(Z|X)}{p(Z)}dz &= E_{q_{\phi}(Z|X)}\{\ln q_{\phi}(Z|X) \} - E_{q_{\phi}(Z|X)}\{p(Z)\}
\end{align}
上記式では、$q_{\phi}(Z|X)$と$p(Z)$のそれぞれに対して$q_{\phi}(Z|X)$で期待値をとったものであることがわかります。そのため、Zの次元数をJとした場合、今回仮定した多変量正規分布を用いてこの式を計算すると以下のようになります。
\begin{align}
KL[q_{\phi}(Z|X)||p(Z)] = - \frac{1}{2} \sum_{j=1}^{J} (1 + \ln \sigma ^{2}_{j} - \sigma ^{2}_{j} - \mu ^{2}_{j})
\end{align}
MNISTデータを用いた実装
Reparameterization trick
ここで、先ほど潜在変数Zの取得について「エンコーダで出力した平均と分散をもとに作られた確率分布から$Z$をサンプリングにより取り出し」と説明しましたが、実際に確率分布からサンプリング操作を行う場合、誤差逆伝播法では勾配を用いて重み修正ができないという問題が生じてしまいます。そのため、この問題を解決するためにReparameterization trickと呼ばれる手法を用いて誤差逆伝播法が可能な形にします。
先ほどの損失関数の導出で使用した確率分布$q_{\phi}(Z|X)$を用いた場合の変形後の式は、以下のようになります。
\begin{align}
Z = \mu + \varepsilon \Sigma
\end{align}
実際に、この式に対して期待値と分散を計算すると(ここでの導出は省きます)、得られる値は$q_{\phi}(Z|X)$の期待値と分散になります。したがって、上記の式を計算するのは、$q_{\phi}(Z|X)$からのサンプリング操作を行うことと同じものとして扱うことができます。
実装
今回はMNISTデータを用いたpytorchによるVAEの実装を行います。なお、使用したコードに関しては、こちらのurlの方のものを参考にさせていただきました。
モデルの部分のプログラムは、以下のようになりました。
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
class VAE(nn.Module):
def __init__(self, x_dim, hidden_dim, z_dim):
super().__init__()
self.enc_1 = nn.Linear(x_dim, hidden_dim)
self.enc_2 = nn.Linear(hidden_dim, hidden_dim)
self.enc_mean = nn.Linear(hidden_dim, z_dim)
self.enc_var = nn.Linear(hidden_dim, z_dim)
self.dec_1 = nn.Linear(z_dim, hidden_dim)
self.dec_2 = nn.Linear(hidden_dim, hidden_dim)
self.dec_3 = nn.Linear(hidden_dim, x_dim)
self.relu = nn.ReLU()
self.sigmoid = nn.Sigmoid()
self.enc_12 = nn.Sequential(
self.enc_1,
self.relu,
self.enc_2,
self.relu,
)
self.dec_123 = nn.Sequential(
self.dec_1,
self.relu,
self.dec_2,
self.relu,
self.dec_3,
self.sigmoid
)
def encode(self, x):
x = self.enc_12(x)
return self.enc_mean(x), F.softplus(self.enc_var(x))
def decode(self, z):
x = self.dec_123(z)
return x
def forward(self, x):
x_mean, x_var = self.encode(x)
z = x_mean + torch.randn(x_mean.shape) * torch.sqrt(x_var)
x = self.decode(z)
return x
def loss(self, x):
x_mean, x_var = self.encode(x)
# KLダイバージェンス(正則化項)
kl = (-0.5) * torch.mean(torch.sum(1 + torch.log(x_var) - x_var - x_mean**2))
# 再構成誤差項
y = self.forward(x)
reconst = torch.mean(torch.sum(x*torch.log(y) + (1-x)*torch.log(1-y)))
return -sum([-kl, reconst])
学習の部分のプログラムは、以下のようになりました。
import numpy as np
from torch import optim
# 記録用の配列
loss_all = np.zeros((2,30))
# 学習
model = VAE(28*28, 300, 10)
optimizer = optim.Adam(model.parameters(), lr=0.001)
model.train()
for i in range(30):
losses = []
losses_val = []
for x, t in dataloader_train:
model.zero_grad()
y = model(x)
loss = model.loss(x)
loss.backward()
optimizer.step()
losses.append(loss.cpu().detach().numpy())
for x_val, t_val in dataloader_valid:
loss = model.loss(x_val)
losses_val.append(loss.cpu().detach().numpy())
# 記録
loss_all[0, i] = np.average(losses)
loss_all[1, i] = np.average(losses_val)
print("EPOCH: {} loss: {}".format(i, np.average(losses)))
実装結果
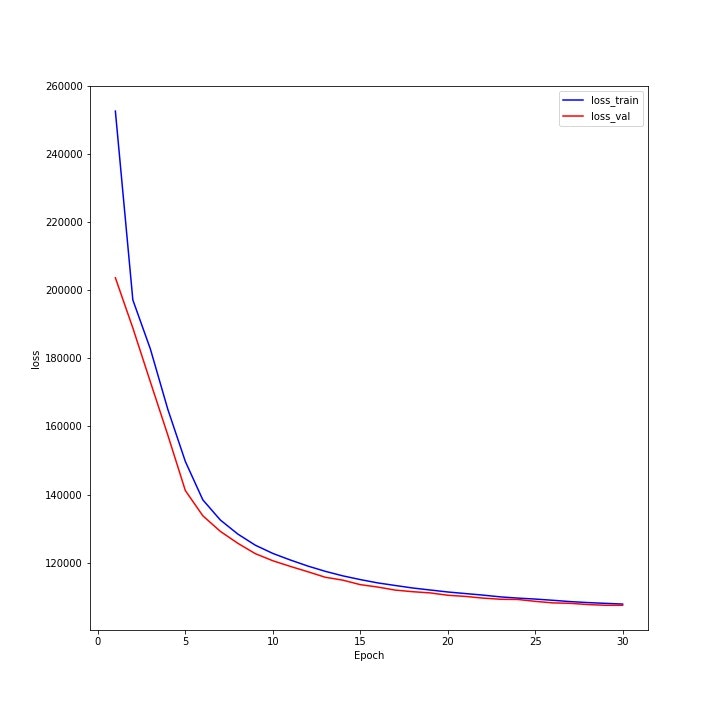
損失関数のグラフ
以下のグラフは、繰り返し回数ごとの学習データと検証データに対する損失関数の値のグラフになっており、学習が進むにつれ低下しているのがわかります。
結果
検証データを用いた際の結果は、以下のようになりました。
画像はそれぞれ、上が10個の検証データで、下がそれに対するモデルの出力になります。
画像を比べると、非常に似たデータを出力できていることがわかります。
次に、ノイズを付与した画像を用いた場合の予測の結果は以下のようになりました。
上は元の検証データに対してランダムで25ピクセルのノイズを追加したデータであり、下はそれに対するモデルの出力になります。
少しぼやけてはいますが、入力データと似たデータを出力できていることがわかります。
また、ノイズが乗った画像と比較すると、実際にノイズの除去に成功したこともわかります。
参考文献
https://jp.mathworks.com/discovery/autoencoder.html
https://www.slideshare.net/ssusere55c63/variational-autoencoder-64515581
https://www.slideshare.net/KazukiNitta/variational-autoencoder-68705109
https://nisshingeppo.com/ai/whats-autoencorder/
https://academ-aid.com/ml/vae
https://academ-aid.com/statistics/kl-div-multi-normal
https://knowwell-livewell.hatenablog.com/entry/2022/02/20/010512
https://arxiv.org/abs/1606.05908
https://www.sambaiz.net/article/212/