HiPPOからVision Mambaまで(1) HiPPOと HiPPO-LegSのアイデア

はじめに

この記事では、最新の深層学習アーキテクチャ Vision Mamba ¹ の論文を理解することを目指して、その前に提唱されてきたアーキテクチャから順を追って読んでいきます。

まず初めに、この記事ではHiPPOという系列データを保持するための構造について取り扱います。そこからS4(Structured State Space Model), Mamba, 最後にVision Mamba という順で説明していきます。

HiPPO

Hippo²は、NeuRIPS 2020 で提唱されたアーキテクチャです。

HiPPOのモチベーションは、「系列データを扱う時に、過去のデータを圧縮して保存したい」ということです。RNNなどのネットワークでは過去の情報を扱いますが、すべてをそのまま保存しておくと計算量が爆発してしまいます。

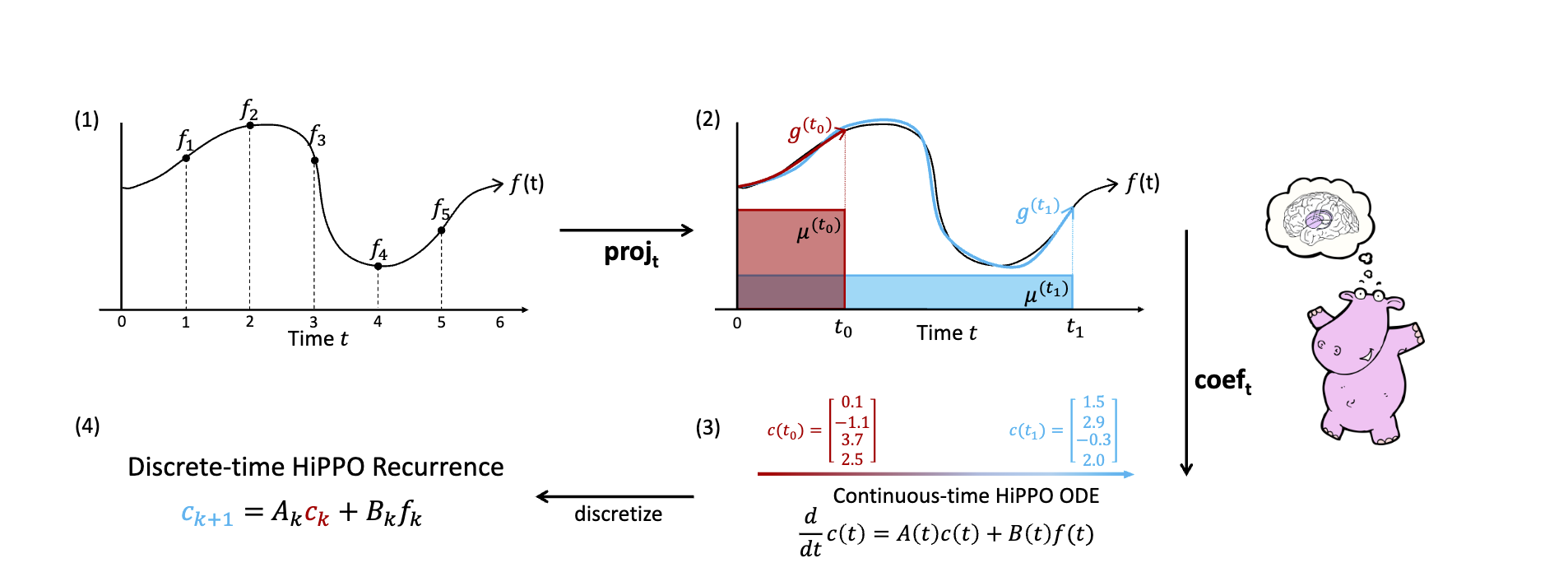
まず、問題を定式化します。ある信号 $f(x)$ の時刻$0$から$t$までのデータ $f_{\leq t}$を圧縮することを考えます。ここで、もっと別の簡単な空間 $\mathcal{G}$ から、 $f_{\leq t}$ にできるだけ近い要素をとってきて、それを$f_{\leq t}$ の代わりにすることで圧縮をしたいです。

つまり、ある集合 $\mathcal{G}$ の要素 $g^{(t)}$ で、$f$との距離 $||f_{\leq t} - g^{(t)}||$ が最小になるものを選びたいです。HiPPOの著者たちは、この$\mathcal{G}$に直交多項式 Orthogonal Polynominalというものを採用しました。

これは要するに、$$a_0 + xa_1 + x^2a_2 + \cdots a_{n-1}x^{n-1}$$ という多項式を使おうということです。でも、多項式のあいだに距離などどうやって定義するのでしょうか？

ここで、線形代数の世界では、多項式はベクトルとみなせることを思い出してください。すなわち、
$$[a_0, a_1, \cdots, a_n] = a_0 + a_1 x + a_2 x^2 + \cdots a_{n-1}x^{n-1}$$ とすればよいです。ふたつの多項式の内積 $\langle f, g \rangle_\mu$ は
$$\langle f, g \rangle_\mu = \int f(x)g(x)d\mu(x)$$
であり、ノルムは

$$||f||_{L_2(\mu)} = \langle f, f {\rangle} _\mu^{1/2}$$
として定義できます。

さて、直交多項式とは、その名の通り直交する多項式の組です。すなわち、

\langle g_i, g_j {\rangle} = \left\lbrace
\begin{array}{ll}1 & \text{if}& i =j 
\\ 0 & \text{if} & i \neq j  
\end{array}
\right.

となるような多項式を$N$個集めたもので、これを基底として用います。
それではHiPPOの話に戻りましょう。ひとまずの目標は、$||f_{\leq t} - g^{(t)}||$を最小にする $g^{(t)}$ を見つけることでした。$g$は適当な多項式ということにして、このような $g$を取ってくる操作を$\text{proj}$ と定義します。
$$\text{proj}_t(f) = \underset{g^{(t)}\in\mathcal{G}}{\arg\min} ||f _{\leq t} - g^{(t)} || _\mu$$
さらに、多項式 $g$ はさきほどの直交多項式の線型結合で表すことができます。この係数を取ってくる操作を $\text{coef}_t$ と定義します。すなわち、直交多項式 $P_1 \cdots P_n$ を用意した時に、 $g^{(t)} = \sum_i P_i(t) c_i(t) $であり、 $\text{coef}_t(g) = [c_1(t), \cdots, c_n(t)]$ とします。

関数$\text{hippo}$ はこの二つの操作の組み合わせです。
$$(\text{hippo}(f))(t) = \text{coef}_t(\text{proj}_t(f))$$

さて、ここまでを一旦まとめると、$\text{HiPPO}$とは、ある入力の今までの状態を多項式で近似して、さらにそれを直交多項式の線型結合で表し、その係数を取り出す操作でした。実は、最終的に欲しい $c(t)$ はもっと簡単に入手することができます。

というのも、この$c(t)$は次のような微分方程式で書けるためです。
$$\frac{d}{dt}c(t)= A(t)c(t) + B(t)f(t)$$
ただし$A \in \mathbb{R}^{N\times N}$, $B \in \mathbb{R}^{N \times 1}$という形の行列とベクトルです。導出については元論文の Appendix D にあるので、一旦こういうものと認めてしまいます。

さらに、この微分方程式の時間を離散化すると、
$$c_{k+1} = A_k c_k + B_k f_k$$
という形に書き下すことができます。

どういうことかというと、まず、ある微小な区間 $h$ をとると、
$$c(t+1) \simeq c(t) + h\frac{d}{dt} c(t)$$
というように書くことができます。（前進オイラー法）
今回は$\frac{d}{dt}c(t)= A(t)c(t) + B(t)f(t)$ なので、代入して
$$c(t+1) \simeq c(t) + h(A(t)c(t) + B(t)f(t))$$
幅を$h = 1$ とおいて書き直すと、
$$c(t+1) \simeq (A(t) + I)c(t) + B(t)f(t)$$
ただし $I$は単位行列です。$A + I$ を再度 $A$ と置き直すことで、一つ先の値も適切な行列 $A$と$B$ があれば計算できることがわかりました。

HiPPO-LegS

今まででHiPPOの基本的なアイデアは書き終わりましたが、適当に直交多項式基底や測度を定めて動かそうとしても、行列$A$や$B$の計算が面倒そうです。そこで、まず基底をルジャンドル多項式、測度を$\mu^{(t)} = \frac{1}{t}\mathbb{1}_{[0,t]}$と定義します。 $\mathbb{1}$ は指示関数です。
ルジャンドル多項式とは、
$$P_n(x) = \frac{1}{2^n n!} \frac{d^n}{d x^n}[(x2-1)^n]$$
という形の$n$次多項式であり、これらは直交形をなすことが知られています。
このとき、行列 $A$, $B$ は明に表すことができます。

A_{nk} = \begin{cases}(2n + 1)^{1/2}(2k + 1)^{1/2} & \text{if} & n>k
\\
n + 1 & \text{if} & n = k 
\\
0 & \text{if} &n < k
\end{cases}

B_{n} = (2n + 1)^{1/2}

ということで、HiPPOという方式で系列データを圧縮する方法について取り扱いました。次回はこれを組み込んだ状態空間モデル、S4について説明します。

1. L. Zhu, B. Liao, Q. Zhang, X. Wang, W. Liu, and X. Wang, Vision Mamba: Efficient Visual Representation Learning with Bidirectional State Space Model. 2024. ↩

2. (Higher-order Polynomial Projection Operations)
   HiPPOは A. Gu, T. Dao, S. Ermon, A. Rudra, and C. Re, HiPPO: Recurrent Memory with Optimal Polynomial Projections. NeuRIPS, 2020. ↩