はじめに：ANSとは？

ANS(Asymmetric Numeral Systems) とは、Duda 2009¹ によって開発されたエントロピー符号化のアルゴリズムです。既存の代表的なアルゴリズムにはハフマン符号化(Huffman Coding)と算術符号化(Arithmetic Coding)がありますが、前者は高速な代わりにコーナーケース（ゼロ埋めされた巨大な配列など）に弱く、後者は圧縮性能が良い代わりに低速です。

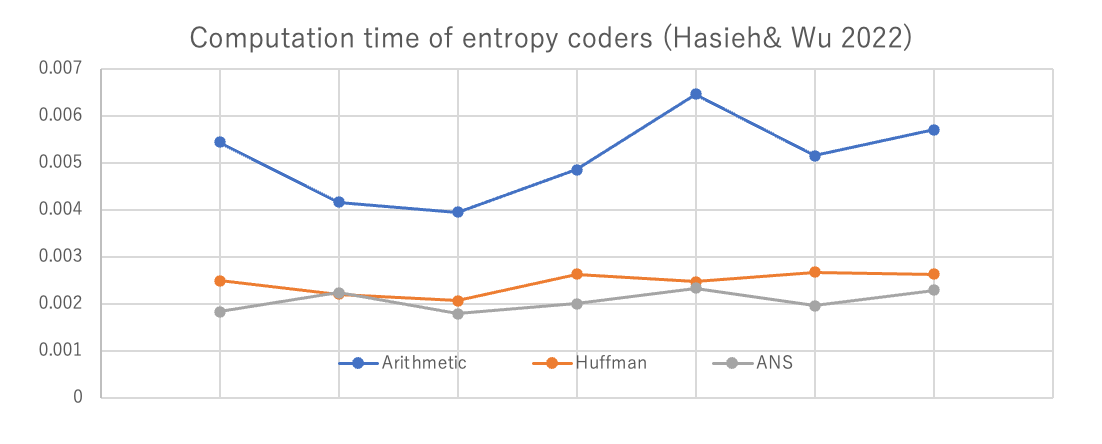
ANSはこの2種類の良いとこどりで、ハフマン符号化に並ぶ速度と算術符号化のパフォーマンスを兼ね備えています。性能を評価した論文に Hsieh & Wu 2022²がありますが、この論文によると次のようなパフォーマンスを示します。

ANSにはいくつかのヴァリエーションがあり、t(table)-ANSや r(range)-ANS などと呼ばれます。この記事ではrANSに的を絞って解説します。以下の解説は、主にTatwawadi氏のWhat is Asymmetric Numeral Systems? ( https://kedartatwawadi.github.io/post--ANS/ ) をもとにしていますが、行間や省かれている証明を大幅に補っています。元の記事にはpythonのコードやその場で動かせるデモがあるので、そちらもご参照ください。また、情報理論の基礎的な部分（シャノンエントロピー、エントロピー符号化）の解説は割愛します。

ANSのバックグラウンド

一般にエントロピー符号化機は、N個のシンボルと各シンボルの発生確率を受け取り、ビット列を出力します。ANSはシンボルを直接ビット列にするのではなく、ある（巨大な）一つの整数に変換します。

簡単な例からはじめます。（やや長いので、冗長そうなら次節に進んで下さい）
入力$\mathcal{S} = \lbrace 3,1,0,9,8\rbrace$だとします。これを整数$x$にする手段として、まず考えられるのは$x = 31098$です。これを符号化するステップを書き下すと、

\begin{align*}
X_1 &= 3 \\
X_2 &= X_1 \times 10 + 1 = 31\\
X_3 &= X_2 \times 10 + 0 = 310\\
X_4 &= X_3 \times 10 + 9 = 3109\\
X_5 &= X_4 \times 10 + 8 = 31098
\end{align*}

さらに、解読の時は


\begin{align*}
X_5 &= 31098 && s_5 =\text{mod}(X_5,10)  = 9 \\
X_4 &= \lfloor{X_5/10\rfloor} = 3109 && s_4 =\text{mod}(X_4,10)  = 4 \\
X_3 &= \lfloor{X_4/10\rfloor} = 310 && s_3 =\text{mod}(X_3,10) = 0 \\
X_2 &= \lfloor{X_3/10\rfloor} = 31 && s_2 =\text{mod}(X_2,10) = 1 \\
X_1 &= \lfloor{X_2/10\rfloor} = 3 && s_1 =\text{mod}(X_1,10) = 3 \\
\end{align*}

このようにすればよいです。
ここで、$\text{mod}(a,b)$とは$a$を$b$で割った剰余を指します。プログラミングでよく a%bと書きますが、qiitaのインライン数式中で\%と打っても出てこなかったのでこうします。
このアルゴリズムはもちろん最適ではありません。すべてのシンボルの分布が等確率ならよいのですが、分布に差があるならそれを反映させる必要があります。
今の操作で、$X_t =X_{t-1} \times 10 + s_i$という操作をしました。これは、「状態$X_{t-1}$を10倍することでシンボル$s_t$の情報だけのブロックを確保して、$s_t$の情報を追加している」、と理解できます。rANSはこの操作を一般化したものだとして説明できます。

記法の説明

rANSの説明の前に、各種記号を定義します。

入力$S$を、$S = (s_1, s_2, ..., s_n)$というn個の記号の列とします。
各$s_i$ は、$\mathcal{A} = \lbrace a_1, a_2, ..., a_k \rbrace$というk個の要素の集合の中に含まれているとします。これは出現しうる記号を定めたもので、アルファベット(Alphabet) と呼びます。
各アルファベットの出現頻度表を $\mathcal{F} = \lbrace F_{a_1}, F_{a_2}, ..., F_{a_k} \rbrace$と表します。これは整数の値を取る必要があり、出現確率（または分布の質量密度関数） $p_i$と、$F_i$の総和$M = \sum_{i=1}^{n} F_i$に対して、$p_i = \frac{F_{a_i}}{M}$が成立します。分布のpmfが与えられている場合、これはpmfに適当な数を掛けるなどして、すべての値が整数になるように近似したものだと捉えられます。
各アルファベットの累積出現頻度 を $C_{a_i} = \sum_{j=1}^{i-1}F_{a_j}$と定義します。これは分布のcdf(累積質量関数)に対応します。
cdfと同様、$C_{a_i}$にも単調増加性があり、$C_{a_1} \leq C_{a_2} \leq ... \leq C_{a_n} \leq M$となります。$M$は全$F_i$の総和なので、どんな$C_{a_i}$も$M$で上から抑えられます。この性質はあとで何度か使います。

rANSのアルゴリズム

エンコーダ側

rANSは先ほどの例と同じように、各状態$X_t$を一つの整数として表します。最終的な出力は$X_n$です。状態を一つ更新させる関数 $\text{encoder}(X_{t-1}, s_t) = X_t$は次のように定義されます。

\begin{align*}
X_t = \left \lfloor \frac{X_{t-1}}{F_{s_t}} \right\rfloor M + C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})
\end{align*}

ただし$M$は先ほども出てきた$F$の総和です。

非常にシンプルで、プログラムでも一瞬で実装できそうな式ですが、何をやっているかは掴みづらいですね。

エンコーダ側のアルゴリズムの説明

直観的な説明を試みます。これは先述した、「前の状態に対して、新しい情報を入れるだけの枠を空けて、新しい情報を入れる」という操作です。
まず、前の状態$X_{t-1}$に対して、Mサイズの「$\lfloor X_{t-1}/F_{s_t}\rfloor$」というブロックを決定します。この値を$\text{BlockID}$と表します。
ここで「新しい情報を入れる」のですが、今回は別に$s_t$が数字とは限りません。なので、その代わりに$[C_{s_t}, C_{s_t+1}-1]$ という区間を使います。cdfが単調増加であるように、$C$も増加性があり、同じ値が同じシンボルに割り振られることはありません。なので、区間$[C_{s_t}, C_{s_t + 1}-1]$と$s_t$の間には一対一の関係が成り立ち、情報として等価です。足す値$C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})$を評価すると、

\begin{align*}
0 &\leq \text{mod}(X_{t-1}, F_{s_t}) < F_{s_t} \\
C_{s_t} &\leq C_{s_t} + \text{mod}(X_{t-1}, F_{s_t}) <F_{s_t} + C_{s_t} \\
C_{s_t} &\leq C_{s_t} + \text{mod}(X_{t-1}, F_{s_t}) < C_{s_t+1} \\ 
(\because &F_{s_t} +  C_{s_t} = F_{s_t} + \sum_{j=1}^{s_t -1}F_j = \sum_{j=1}^{s_t}F_j = C_{s_t+1}) 
\end{align*}

となって、確かにこの区間に収まっています。この区間のことを$\text{slot}$と書くことにします。すると、エンコーダの式は

X_t = \text{BlockID} \times M + \text{slot}

と表せます。先の例で出した$X_t = X_{t-1}\times 10 + s_t$と同じような形になりました。

デコーダ側

前に見た例と同じように、デコーダ側はエンコーダと逆の向きから値を解読していきます。したがって、形式的には次のような形の関数となります。

X_{t-1}, s_t = \text{decoder}(X_t)

先ほど、シンボルとその累積出現頻度は一対一だと述べました。なので$C_{s_t}$から$s_t$への逆変換があるはずで、これを$C_{\text{inv}}(y)$という関数として表します。形式的には、$C_\text{inv}(y) = a_i \text{ if } C_{a_i} \leq y < C_{a_i + 1}$です。この上で、デコーダの式は次のように表せます。

\begin{align*}
\text{slot} &= \text{mod}(X_t, M) \\
s_t &= C_{\text{inv}}(\text{slot})\\
X_{t-1} &= \left\lfloor \frac{X_t}{M}\right\rfloor\times F_{s_t} + \text{slot} - C_{s_t}
\end{align*}

デコーダ側のアルゴリズムの説明① slotの復元

こちらもなぜデコードできるか説明をします。まず、エンコーダの式は次のようでした。

\begin{align*}
X_t = \left \lfloor \frac{X_{t-1}}{F_{s_t}} \right\rfloor M + C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})
\end{align*}

そして、これは $X_t = \text{BlockID}\times M + \text{slot}$ という形で書き表すこともできました。
ということで、デコーダは現在の状態$X_t$と、事前に与えられた$F_{s_k}$, $C_{s_k}$, $M$の情報を用いて、$\text{BlockID}$と$\text{slot}$を特定する必要があります。

まず、$\text{slot} = C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})$は$\text{slot} = \text{mod}(X_t, M)$ として復元できます。なぜならエンコーダの式より、

\begin{align*}
\text{mod}(X_t, M) &= \text{mod}\left(\left \lfloor \frac{X_{t-1}}{F_{s_t}} \right\rfloor M + C_{s_t} + \text{mod}(X_{t-1}, F_{s_t}), M \right) \\
&= \text{mod}\left(C_{s_t} + \text{mod}(X_{t-1}, F_{s_t}), M \right)  \\
&=C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})\\
&= \text{slot}
\\
\end{align*}

ただし、1行目から2行目の変形には$\lfloor{X_{t-1}}/{F_{s_t}} \rfloor \times M$が$M$の倍数であることを用いていて、2行目から3行目の変形には$C_{s_t} + \text{mod}(X_{t-1}, F_{s_t}) < C_{s_t+1}$が（先程のエンコーダ側の不等式の計算より）成り立ち、なおかつ $C_{s_t+1} \leq M$であることから、$C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})$が$M$より小さいことを用いています。

さて、$\text{slot}$がわかったら、シンボル$s_t$を$s_t = C_{\text{inv}}(\text{slot})$として一意に復元できます。ここから$F_{s_t}$と$C_{s_t}$の値が使えるようになるので、これらを用いて$X_{t-1}$を復元していきます。

デコーダ側のアルゴリズムの説明② 状態Xの復元

まず事前準備として、$\lfloor X_t/M \rfloor = \lfloor X_{t-1}/F_{s_t} \rfloor$を示します。

\begin{align*}
\left\lfloor \frac{X_t}{M} \right\rfloor &= \left\lfloor \frac{\left \lfloor \frac{X_{t-1}}{F_{s_t}} \right\rfloor M + C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})}{M} \right\rfloor\\

&=\left\lfloor  \left\lfloor\frac{X_{t-1}}{F_{s_t}}\right\rfloor +   \frac{C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})}{M} \right\rfloor\\

&= \left\lfloor\frac{X_{t-1}}{F_{s_t}}\right\rfloor &\left(\because 0 \leq \frac{C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})}{M} < 1\right)
\end{align*}

最後の変形では先程も使った不等式、$C_{s_t} + \text{mod}(X_{t-1}, F_{s_t}) < M$の両辺をMで割ったものを用いています。
それでは$X_{t-1}$の計算に移りましょう。まず一般に、自然数$a,b$に対して$a = \lfloor a/b \rfloor \times b + \text{mod}(a,b)$が成立します。$a = X_{t-1}, b = F_{s_t}$として、

\begin{align*}
X_{t-1} &= \left\lfloor\frac{X_{t-1}}{F_{s_t}}\right\rfloor \times F_{s_t} + \text{mod}(X_{t-1}, F_{s_t}) \\
& = \left\lfloor\frac{X_{t}}{M}\right\rfloor \times F_{s_t} + \text{mod}(X_{t-1}, F_{s_t})\\
&= \left\lfloor\frac{X_{t}}{M}\right\rfloor \times F_{s_t} + \text{mod}(X_{t}, M) - C_{s_t}
\end{align*}

ここで1,2行目の変形には先に示した$\lfloor X_t/M \rfloor = \lfloor X_{t-1}/F_{s_t} \rfloor$を使っており、2,3行目の変形には$\text{slot}$の解読のときに示した$\text{slot} = C_{s_t} + \text{mod}(X_{t-1}, F_{s_t}) = \text{mod}(X_t, M)$を用いています。これは確かにデコーダの式に一致します。これでエンコーダに対してデコーダが正しく動作することが保証できました。

エントロピー的な最適性の証明

ここまでで、rANSの符号化と復号化の仕組みを説明し終わりました。次に、この仕組みがエントロピー的に最適であることを示します。シャノンの情報源符号化定理より、ある情報$S$の符号化の下限は$S$の情報エントロピーを$H(S)$としたとき、$nH(S)$に等しいです。符号化後の$X_t$のビット表現がこのシャノン限界にしたがっていることを示したいので、いま示すべき式は次のように表せます。

\begin{align*}
E[\log X_n] \approx  -n\sum_{i=1}^{k} p(s_i) \log p(s_i)
\end{align*}

まず、一回の更新ごとに増える情報量 $\log X_{t}/X_{t-1}$ を評価します。

\begin{align*}
\frac{X_t}{X_{t-1}} &= \frac{\left \lfloor \frac{X_{t-1}}{F_{s_t}} \right\rfloor M + C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})}{X_{t-1}} \\
&\approx \frac{\frac{X_{t-1}}{F_{s_t}} M + C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})}{X_{t-1}}
\\
&= \frac{M}{F_{s_t}} + \frac{C_{s_t} + \text{mod}(X_{t-1}, F_{s_t})}{X_{t-1}} \\
& \leq \frac{M}{F_{s_t}} +\frac{M}{X_{t-1}}
\end{align*}

$X_{t-1}$の値は$t$が大きくなるにつれて大きくなるので、ここでは十分大きいものとして、$M/X_{t-1} \approx 0$と（雑に）近似してしまいます。したがって、

\begin{align*}
\frac{X_t}{X_{t-1}} &\approx \frac{M}{F_{s_t}} \\&= \frac{1}{p(s_t)}
\end{align*}

となって、更新一回ごとに増える情報量$\log X_t - \log X_{t-1}$は、おおむね追加するシンボル$s_t$の情報量$-\log p(s_t)$になります。これより、$X_n$について計算すると、

\begin{align*}
X_n &= \frac{X_n}{X_{t-1}} \times \frac{X_{n-1}}{X_{n-2}} \times ... \times \frac{X_{2}}{X_{1}}\\
&\approx \frac{1}{p(s_n)}\frac{1}{p(s_{n-1})}...\frac{1}{p(s_2)}\frac{1}{p(s_1)}
\end{align*}

\begin{align*}
\log X_n&\approx  \sum_{t=1}^n -\log p(s_t)
\end{align*}

各シンボルの出現確率を考えると、平均して一回ごとの情報量は

\begin{align*}
E[\log X_t - \log X_{t-1}] &= E[-\log p(s_t)]\\
&= \sum_{i=1}^{k}- p(s_i) \log p(s_i)
\end{align*}

また、各要素のi.i.d性より、$X_n$の長さの期待値は

E[\log X_n] \approx -n\sum_{i=1}^{k} p(s_i) \log p(s_i)

となって、たしかにシャノンエントロピーに近いようです。
今のは非常におおまかな議論ですが、Duda 2013の論文³ではもっと正確に、シャノンエントロピーからのずれ$\Delta H$を計算して、ハフマン符号化よりも定量的に優れていることを示しています。

実装上の工夫

rANSはGithubなどにいくつかの実装があり、Fabian "ryg" Giesen氏によるryg-rANS(https://github.com/rygorous/ryg_rans )などがよく用いられているようです。こうしたコードを見ると、符号化と復号化で$M$を乗算する部分はビットシフトを用いて
C(x,s) = (floor(x / f[s]) << n) + (x % f[s]) + C[s]
D(x) = (f[s] * (x >> n) + (x & mask ) - C[s], s)

のように書かれることが多いです。Wikipediaの解説もこうなっています。これは掛け算をビットシフトに、$C_\text{inv}$の計算をビットマスクにして計算を高速化するためです。
思い出してほしいのですが、各要素のpmf $p(s_i)$に対して $F_{s_i}$を作るときは、何らかの数$M$を用いました。この$M$に特に制約はないので、これを$M = 2^R$の形にすることができます。すると

\begin{align*}
\left \lfloor \frac{X_{t-1}}{F_{s_t}} \right\rfloor M  &= \left \lfloor \frac{X_{t-1}}{F_{s_t}} \right\rfloor << R
\\
\left \lfloor \frac{X_{t}}{M} \right\rfloor  &= X >> R\\
\text{slot}= \text{mod}(X_t, 2^R) &= X_t \& (2^R - 1)
\end{align*}

ただし&はビットANDです。最後に関しては、例えば$M = 8 = 1000_2$で$X = 14 = 1110_2$のとき、modをとった答えは$6 = 110_2$です。つまり、$2^R$でmodを取る操作は、値の後ろの$R$ビットだけを取り出す操作に相当するので、これは$2^R-1$とのビットANDを取ることで計算できます。

他の実装上の詳細に関しては、ryg氏のブログ（https://fgiesen.wordpress.com/ ）に詳しく書いてあります。

おわりに

ここまで読んでいただいてありがとうございます。自分の勉強を兼ねて書いたものなので、各所に不十分な説明や誤りがある可能性があります。お気軽にコメントや編集リクエストをいただけると幸いです。

Jarek Duda, "Asymmetric numeral systems", 2009, https://arxiv.org/abs/0902.0271 ↩
P. A. Hsieh and J.-L. Wu, “A Review of the Asymmetric Numeral System and Its Applications to Digital Images,” Entropy, vol. 24, no. 3, Art. no. 3, Mar. 2022, doi: 10.3390/e24030375. ↩
Jarek Duda, "Asymmetric numeral systems: entropy coding combining speed of Huffman coding with compression rate of arithmetic coding", 2014, https://arxiv.org/abs/1311.2540 ↩

rANS(range variant of Asymmetric Numeral Systems) 入門