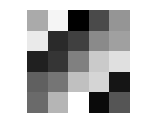目次へのリンク
概要
MATLABによる画像の取扱いを見ていきます。画像は行列操作とみなせますのでMATLABが得意な領域です。
対応ファイル:I1_01_commandline.m
四則演算、代入、セミコロン
MATLABはインタプリタ型の言語ですので、コマンドウィンドウでリターンキーを押すことで結果をすぐに見ることができます。
2+3
ans = 5
変数定義不要です。
a=2+3
a = 5
セミコロンを付けると結果を表示しません。
a=2+3;
行列操作による画像の取扱い
ここでは、magicという関数を用い、1から25の数を一回ずつ使い、縦・横・斜めどこを足し合わせても、同じ数になる、魔方陣という行列を生成してみます。
>> magic(5) % 先ず、5行5列の行列を生成します。
ans = 5x5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
行列を変数Aに代入
MATLABは変数の定義が必要ありませんので、このように、変数Aに代入することで変数が自動的に作成されます。
A=magic(5)
A = 5x5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
行列を画像として表示
MATLABには、可視化用の様々な関数が用意されています。 ここではimshowという関数を用いて表示したいと思います。 1が真っ黒・最大値の25が真っ白として表示します。
imshow(A, [],'InitialMagnification','fit');
このように画像が表示されますが、行列のそれぞれの要素の値が、各Pixelの明るさに対応していて、2次元行列と画像が1:1に対応していることが分かります。
10以下のものを除去し、10より大きなものは残す
MATLABでは行列のまま取り扱えますので、簡潔な記述で処理をすることができます。MATLABでは、行列に対する様々な便利な演算子が用意されており、例えば、行列の各要素と、数値10を比較したいときには、比較演算子が使えます。
B=A<10
B = 5x5 の logical 配列
0 0 1 1 0
0 1 1 0 0
1 1 0 0 0
0 0 0 0 1
0 0 0 1 1
このように、行列と数字10を比べてやることで、10よりも小さい要素位置には1、10以上のところは0になった行列を得ることができます。
MATLABでは小かっこで要素を指定
例えば、行列のAの第1行・1列目を指定するには小かっこを用います。
A(1,1)
ans = 17
要素の指定には行列を使うことも可能
要素指定部分に、B行列をつかうとB行列の1のところの要素のみ取り出すことができます。
A(B)
ans = 9x1
4
5
6
1
7
8
2
3
9
B行列の1の要素に対してのみ処理を実行
要素指定部分にB行列を使い、代入を行うことも可能です。
A(B)=1
A = 5x5
17 24 1 1 15
23 1 1 14 16
1 1 13 20 22
10 12 19 21 1
11 18 25 1 1
可視化して確認
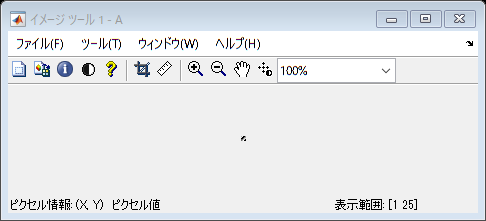
画像解析の機能が豊富な、imtoolという別のツールを使ってみます。
imtool(A, []);
灰色部分が値1になり真っ黒になっていることが分かります。右下に、マウスの座標やその位置の値が表示されます。定規アイコンで距離を測ることもできますし、イメージ の下の ピクセル領域 というメニューを使うと、このように各Pixelの明るさの値を表示することもできます。カラーの場合は、3つの値が表示されます
行列をスカラーと同様に扱える
A+10
ans = 5x5
27 34 11 11 25
33 11 11 24 26
11 11 23 30 32
20 22 29 31 11
21 28 35 11 11
sin(A)
ans = 5x5
-0.9614 -0.9056 0.8415 0.8415 0.6503
-0.8462 0.8415 0.8415 0.9906 -0.2879
0.8415 0.8415 0.4202 0.9129 -0.0089
-0.5440 -0.5366 0.1499 0.8367 0.8415
-1.0000 -0.7510 -0.1324 0.8415 0.8415
飽和処理も自動で行ってくれる
符号なし8bit整数型(uint8)はデフォルトで飽和処理が有効になっています。意図しないオーバーフローを防いでくれます。
a = uint8(255)
a = 255
a + 1
ans = 255
論理インデックスの活用
A行列と10を比べて作ったB行列を画像として表示してみます。
B
B = 5x5 の logical 配列
0 0 1 1 0
0 1 1 0 0
1 1 0 0 0
0 0 0 0 1
0 0 0 1 1
imshow(B,[],'InitialMagnification','fit');
10よりも小さい要素は白、10より大きい要素は黒の二値画像になっていて、大小比較演算だけで2値画像が作れることが分かります。その他にも、例えば、ある行列の一部を0にしたい場合は下記のように~(論理否定)が使えます。
B % このようなB行列の1のところを、先ほどのように1にするのではなく0にしたい場合
B = 5x5 の logical 配列
0 0 1 1 0
0 1 1 0 0
1 1 0 0 0
0 0 0 0 1
0 0 0 1 1
~B % チルダで、行列の0, 1を反転
ans = 5x5 の logical 配列
1 1 0 0 1
1 0 0 1 1
0 0 1 1 1
1 1 1 1 0
1 1 1 0 0
A % A行列を確認
A = 5x5
17 24 1 1 15
23 1 1 14 16
1 1 13 20 22
10 12 19 21 1
11 18 25 1 1
A .* ~B % チルダB の各行列の要素同士の掛け算 (*の前に.を置くことで出来ます)
ans = 5x5
17 24 0 0 15
23 0 0 14 16
0 0 13 20 22
10 12 19 21 0
11 18 25 0 0
目次へのリンク
参考
謝辞
本記事は@eigsさんのlivescript2markdownを使わせていただいてます。