ZOZOテクノロジーズその2 Advent Calendar 2018 の23日目の記事になります．

今回は独学で学ぼうとするとつまずきやすい自己組織化マップについて要点をまとめたいと思います．機械学習の初学者向けに知識共有ができればと考えています．
もし興味をもたれた方は，こちらのサイトにある解説ドキュメントの『自己組織化マップ入門¹』により詳しく書かれていますので，是非読んでみてください．

問題設定

（数式をいくつか出しますが，ひとまず図をざっくり理解してもらえれば大丈夫です．大雑把に言えば「データセットが与えられたときにその潜在変数と(潜在空間から観測空間への)写像を推定しましょう」という話です．）

まず与えられる $N$ 個の観測データを $\mathbf X = \{\mathbf x_n \}^N_{n=1}, \ \mathbf x_n \in \mathcal X$ とします．ここで $\mathcal X$ は高次元の観測空間で， $D$次元のユークリッド空間とします．つまり $\mathcal X = \mathbb R^D$ であり，データ全体は $\mathbf X \in \mathbb R^{N \times D}$ と表せます．
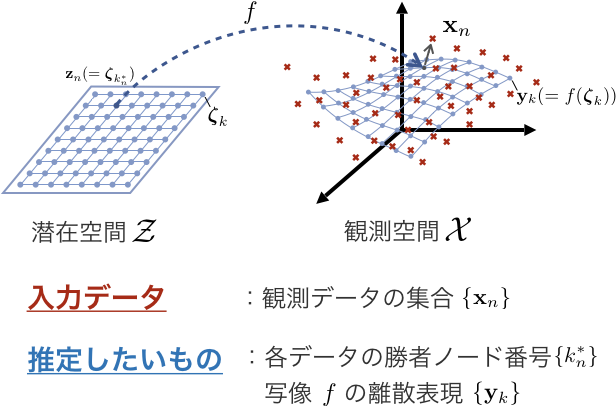
図を書くと以下のような感じですね．

これらのデータが 潜在変数 $\mathbf Z = \{\mathbf z_n \}^N_{n=1}, \ \mathbf z_n \in \mathcal Z$ と写像 $f:\mathcal Z \longrightarrow \mathcal X$ によって， $\mathbf x_n = f(\mathbf z_n) + \boldsymbol \varepsilon_n$ という形式で生成される，と仮定します．ここで $\mathcal Z$ は低次元の潜在空間であり，潜在空間の次元 $L$ は観測空間の次元よりも小さい $(L \lt D)$ とします．また写像 $f$ は滑らかな非線形写像とします．この仮定のもとで， 潜在変数 $\{\mathbf z_n \}^N_{n=1}$ と写像 $f$ を推定することが目的となります．
ここまでの目的を概念図にすると以下のような感じです．

これはSOMに限らず 潜在変数モデル の基本的な枠組みの一つです．

SOMではこの推定タスクを実現するために，さらにこのモデルに制約を加えます．
まず潜在空間 $\mathcal Z$ を閉区間とします（下のpython実装ではその領域については $\mathcal Z = [-1, 1]^L$ としてあります）．
次に潜在空間全体を $K$ 個の代表点（これをノードと呼ぶ）で離散表現します． $k$ 番ノードの座標を $\boldsymbol \zeta_k \in \mathcal Z$ とおきます．
これらの制約によって，写像 $f$ 全体は各ノード座標 $\{ \boldsymbol \zeta_k \}^K_{k=1}$ からの $K$ 個の写像 $\mathbf y_k = f(\boldsymbol \zeta_k)$ によって離散表現できます（この$\mathbf y_k$を参照ベクトルと呼ぶ）．
また，各データの潜在変数 $\mathbf z_n$ は $\{\boldsymbol \zeta_1, \cdots, \boldsymbol \zeta_K\}$ のいずれかとなるため， $\mathbf z_n$ に対応するノード（これを勝者ノードと呼ぶ）のノード番号さえわかれば良いということになります． $\mathbf z_n$の勝者ノードのノード番号を $k^*_n$ と記述します．
以上の制約により，上記の 潜在変数 $\{\mathbf z_n \}^N_{n=1}$ と写像 $f$ の推定 という問題設定が 勝者ノード番号 $\{k^*_n\}^N_{n=1}$と写像の離散表現 $\mathbf Y$ の推定 におきかわります．

以上を踏まえて，SOMの概念図は以下の通りです．

これを（広義の）EMアルゴリズムにより推定します．

アルゴリズム

アルゴリズムの説明や導出などの詳細については『自己組織化マップ入門¹』をご覧ください．
実装するものは以下の3つの手続きです．
はじめに初期化をしたのち，E step と M step を繰り返します．

初期化
$\mathbf Y$ の初期値をPCAにより求めます．

E step
現在の参照ベクトル集合 $\mathbf Y$ の情報をもとに，勝者ノードのノード番号 $\{k^*_n\}$の推定をします．
それに合わせて潜在変数 $\{\mathbf z_n \}$ の推定値も求めます．

\begin{eqnarray}
\forall n, \qquad k^*_n &=& \mathop{\rm arg\,min}_k \| \mathbf x_n - \mathbf y_k \|^2 \\
\mathbf z_n &=& \boldsymbol \zeta_{k^*_n} 
\end{eqnarray}

M step
現在の潜在変数 $\{\mathbf z_n \}$ の情報をもとに，参照ベクトル集合 $\mathbf Y$ の推定をします．

\begin{eqnarray}
\forall n,k, \qquad r_{nk} &=&  \exp \left( - \frac{1}{2 \sigma^2(t)} \| \mathbf z_n - \boldsymbol \zeta_k \|^2\right) \\
\forall k, \qquad \mathbf y_k &=& \frac{\sum_n r_{nk} \mathbf x_n}{\sum_{n'} r_{n'k}}
\end{eqnarray}

ここで $r_{nk}$ は各勝者ノードが近傍のノードに分配する学習量です．
また， $\sigma(t)$ は潜在空間上での近傍領域の大きさを決めるパラメータで，近傍半径と呼ばれます．学習回数 $t$ とともに減少していく関数を使えば良いです．

以上がSOMのアルゴリズムになります．

なお，近傍半径に使う関数の選択によって学習にかかる時間や結果の安定性などをある程度コントロールできます．この辺りはこれが正しいというような絶対的な関数はなく，どの関数を使うかは解析者に委ねられています．『自己組織化マップ入門¹』では以下の関数を提案しています．

\sigma(t) = \max\left[\sigma_0\left(1-t/\tau\right), \sigma_{\rm min}\right] \tag{1}

\sigma(t) = \max\left[\sigma_0\exp\left(-t/\tau\right), \sigma_{\rm min}\right] \tag{2}

今回は以下のような単調減少関数にしました．

\sigma(t) = \sigma_{\rm min} + (\sigma_0 - \sigma_{\rm min}) \exp \left(-\frac{t}{\tau} \right) \tag{3}

なお $\sigma_0 = 1.0, \sigma_{\rm min} = 0.2, \tau = 20.0$ としたときの上記3つの近傍半径の値の変動は以下のグラフのようになります．

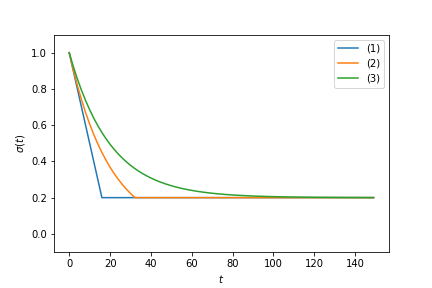
(3)式の場合，近傍半径が減少し続けるため推定値も変動し続けることになります．このため学習の終了条件を決めておく必要があります．今回は図や式から考えて， $5\tau$ あたりまで学習を進めれば十分そうかなと考え，そのように実装してあります．
(1), (2)式の場合は特定の値で減少がストップするようになっており，いずれ推定値の変動も無くなります．このため，変動がなくなったタイミングで学習を終了するといった終了条件が使えるようになり，終了タイミングを気にしなくてよくなります．

実装

上記のアルゴリズムを元にSOMクラスを実装しました．（実装がややこしくなりそうだったので潜在空間は2次元限定としました）
_e_step(self, X) や _m_step(self, X, t) などは上記のアルゴリズムとの対応関係を意識して書いています．

SOM.py

import numpy as np
from scipy.spatial.distance import cdist
from sklearn.decomposition import PCA


class SOM(object):
    def __init__(self,
                 n_components=2,
                 resolution=20,
                 sigma_max=1.0,
                 sigma_min=0.2,
                 tau=20.0,
                 max_iter=100):
        if n_components != 2:
            raise (NotImplementedError())
        self.n_components = n_components
        self.resolution = resolution
        self.sigma_max = sigma_max
        self.sigma_min = sigma_min
        self.tau = tau
        self.max_iter = max_iter

        self.y = None
        self.z = None
        self.k_star = None
        self.zeta = None

    def fit(self, data):
        self._initialize(data)
        for t in range(self.max_iter):
            self._e_step(data)
            self._m_step(data, t)

    def _initialize(self, data):
        self.zeta = create_zeta(self.resolution, self.n_components)
        pca = PCA(n_components=self.n_components)
        pca.fit(data)
        self.y = pca.inverse_transform(np.sqrt(pca.explained_variance_)[None, :] * self.zeta)

    def _e_step(self, data):
        self.k_star = np.argmin(cdist(data, self.y, 'sqeuclidean'), axis=1)
        self.z = self.zeta[self.k_star, :]

    def _m_step(self, data, t):
        r = np.exp(-0.5 * cdist(self.zeta, self.z, 'sqeuclidean') / (self._sigma(t) ** 2))
        self.y = np.dot(r, data) / np.sum(r, axis=1)[:, None]

    def _sigma(self, epoch):
        return self.sigma_min + (self.sigma_max - self.sigma_min) * np.exp(- epoch / self.tau)


def create_zeta(resolution, n_components):
    if n_components != 2:
        raise (NotImplementedError())
    mesh1d, step = np.linspace(-1, 1, resolution, endpoint=False, retstep=True)
    mesh1d += step / 2
    meshgrid = np.meshgrid(mesh1d, mesh1d)
    return np.dstack(meshgrid).reshape(-1, 2)

試してみた

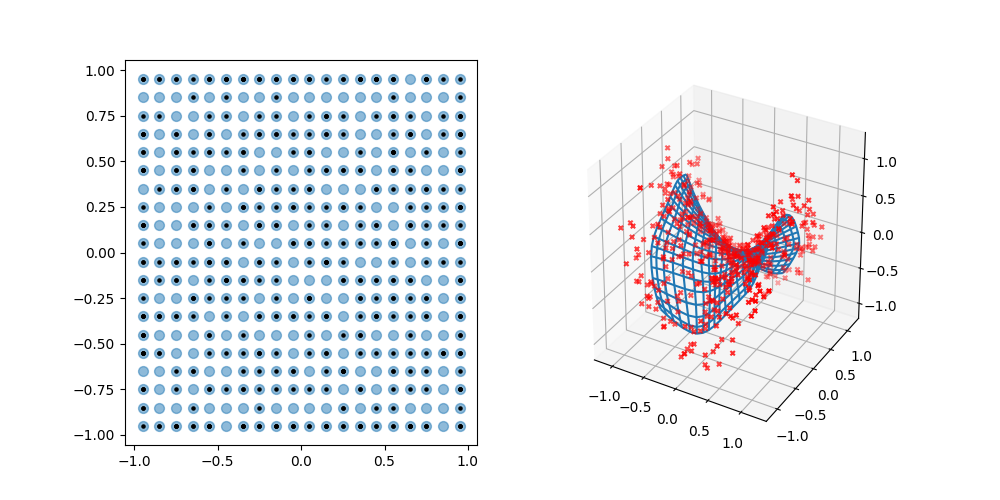
問題設定に合わせて人工データを作り，概念図と同じような結果が得られるのか試してみました．

example.py

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from SOM import SOM


def main():
    # create data
    input_dim = 3
    latent_dim = 2
    n_samples = 500
    noise = 0.1
    random_seed = 100

    np.random.seed(random_seed)
    z = np.random.uniform(-1, 1, size=(n_samples, latent_dim))
    data = np.empty((n_samples, input_dim))
    data[:, 0] = z[:, 0]
    data[:, 1] = z[:, 1]
    data[:, 2] = z[:, 0] ** 2 - z[:, 1] ** 2
    data += np.random.normal(scale=noise, size=(n_samples, input_dim))

    # learning
    som = SOM()
    som.fit(data)

    # plot result
    fig = plt.figure(figsize=(10, 5))
    ax_latent = fig.add_subplot(121)
    ax_latent.scatter(som.zeta[:, 0], som.zeta[:, 1], s=50, alpha=0.5)
    ax_latent.scatter(som.z[:, 0], som.z[:, 1], s=5, color='black')
    wf = som.y.reshape(20, 20, 3)
    ax_observable = fig.add_subplot(122, projection='3d')
    ax_observable.plot_wireframe(wf[:, :, 0], wf[:, :, 1], wf[:, :, 2])
    ax_observable.scatter(data[:, 0], data[:, 1], data[:, 2], marker='x', color='red', s=10)
    plt.show()


if __name__ == '__main__':
    main()

これを実行すると以下のような結果が得られます．

いい感じですね！

Q&A

少し学んだことのある方にとって疑問となりそうなトピックをいくつか挙げておきます．
これらの疑問の多くは，今回の話が工学的な実応用の側面からSOMを活用する立場を取っていることに由来します．

アルゴリズムが知っているのとなんか違う気がする？

この疑問をもつ方はおそらくオンライン学習のSOMのみを知っているのだと思われます．
多分こんな感じの式を知っているのではないでしょうか？

\mathbf y_k^{(t+1)} = \mathbf y_k^{(t)} + \alpha^{(t)} r_k^{(t)} \left( \mathbf x^{(t)} - \mathbf y_k^{(t)} \right)

このような式はオンライン学習のバージョンのSOMに登場します．
今回説明したのはバッチ学習のバージョンのSOMです．

適当に検索すると，オンライン学習のみを簡易的に解説・実装した記事によく当たってしまいます．
ではなぜ今回バッチ学習の方を説明したのかというと，そのほうが実応用に適しているからです．
SOMの創案者であるKohonenは"Essentials of the self-organizing map²"で以下のように述べています．

The actual computations for producing the ordered set of the SOM models can be implemented by either of the following main types of algorithms: 1. The models in the original SOM algorithm are computed by a recursive, stepwise approximation process in which the input data items are applied to the algorithm one at a time, in a periodic or random sequence, for as many steps as it will be necessary to reach a reasonably stable state. 2. In the batch-type process, on the other hand, all of the input data items are applied to the algorithm as one batch, and all of the models are updated in a single concurrent operation. This batch process usually needs to be reiterated a few to a few dozen times, after which the models will usually be stabilized exactly. Even the time to reach an approximately stabilized state is an order of magnitude shorter than in the stepwise computation.
It should be emphasized that only the batch-learning version of the SOM is recommendable for practical applications, because it does not involve any learning-rate parameter, and its convergence is an order of magnitude faster and safer.

このように実応用としてSOMを利用する場合は様々な観点からバッチ学習のバージョンが推奨されています．
メモリにのらないくらい学習データのサンプルが莫大なケースでもない限りは，バッチ学習のSOMを採用しましょう．

学習データが莫大なケースの場合はミニバッチ学習にするのをおすすめします．

こんな問題設定だったっけ？

SOMはシンプルなアルゴリズムなので，いくつかの問題設定からアルゴリズムを説明できます．
今回は機械学習の観点から，特に連続潜在変数モデルの観点から問題設定を説明しています．

他の説明方法もあって，例えばベクトル量子化（クラスタリングの一種）に位相構造を導入したものとも見なせます．
この場合，k-means法のアルゴリズムと比較してみるのがわかりやすいです．
k-means法のアルゴリズムは $\{\mathbf y_k\}$ の初期化と以下の繰り返しです．

\begin{eqnarray}
k^*_n &=& \mathop{\rm arg\,min}_k \| \mathbf x_n - \mathbf y_k \|^2 \\
r_{nk} &=&  
\begin{cases}
 1 & {\rm if} \ k = k^*_n \\
 0 & {\rm otherwise}
\end{cases} \\
\mathbf y_k &=& \frac{\sum_n r_{nk} \mathbf x_n}{\sum_{n'} r_{n'k}}
\end{eqnarray}

繰り返し部分をSOMのアルゴリズムと比較すると，ちょうど $r_{nk}$ のところだけ異なります．
すなわち，k-means法にクラスタ間の位相構造を情報として導入したのがSOM，と説明することもできます．

また，歴史的には大脳視覚野の自己組織化現象を説明するための数理モデルというのがSOMの出発点になっており，神経回路モデルを用いた説明が初期に行われてきました．

六角形がたくさん並んでいるのを見たことがあるけどそれとは違うの？

これは潜在空間上の代表点をどう配置するのかの違いです．六方格子状に分割して配置した場合，結果の表示のときに六角形をたくさん並べて表示することになります．等確率密度関数の形成という点では正方格子よりも正確な配置となりますが，アルゴリズム面での本質的な違いはありません．
充分な代表点数があればどちらを選択しても大きな影響はないと思いますが，個人的な意見を書くと正方格子の方がシンプルで好きです．上記人工データ検証結果のような観測空間上の写像のメッシュ表示でもジグザグにならずに済みます．

初期化は乱数じゃないの？

これは視覚神経モデルの観点からは重要な話で，ランダムな初期状態から自己組織的にマップを形成することは，神経系の自己組織的機能分化の現象を数理モデル的に解明しようという試みの一環に通じます．確かに個人的な経験則ではありますが，SOMは初期値の設定が少し悪い状況下でもそこまで結果に悪影響を与えなかったりします．
とはいえ，今回はあくまで工学的応用の観点に立っているので，無理に悪い条件から進める必要はありません．PCAなどの線形モデルの結果を初期値に用いるのは乱数よりは良い選択かなと思います．

まとめ

自己組織化マップについて問題設定から実装までを概括し，Q&Aをいくつかまとめました．参考になれば幸いです．
今回取り上げられなかった疑問やその他詳細について知りたい場合は，引用した文献を参考にするのをオススメします．

http://www.brain.kyutech.ac.jp/~furukawa/data/SOMtext.pdf ↩ ↩² ↩³
T. Kohonen, Essentials of the self-organizing map, Neural Networks 37 (2013) 52–65. ↩

自己組織化マップ (Self-Organizing Map: SOM) について概括する