はじめに
こんにちは。今年の東洋のサンタクロースを担当いたします。トコロテン🎅です。
本記事では、プログラム初心者の登竜門である†再帰†についてお話しします。
また、記事内に登場するプログラムはJavaにて実装されています。
例外処理等、ロジックと本質的に関係ない部分は省きました。
対象者
幼女「再帰ってなぁ〜に?」
対象者「ばなな」
以上の条件を満たす方を対象者として想定しています。
注意点
本記事では、理解を第一に優先します。
そのため、厳密な定義や説明はいたしません。
また、簡単化するためにあえて触れない部分や、厳密ではない数学的な説明、分かりやすくするために本来のコンピュータの挙動とは少し異なった説明をする場合があります。
完璧に理解したい、100%正しい知識を得たい方は今すぐこの記事を閉じることをおすすめいたします。
再帰とは
プログラムにおける再帰も数学における再帰も本質的な意味合いは同じです。
再帰とは**「自身を定義する際に自身を利用すること」を指します。
また、再帰的に定義された関数を再帰関数**と呼びます。
いろいろな再帰関数
多くのものは再帰的に表現することができますが、今回は代表的な再帰関数の例を取り上げます。
数学的な定義とプログラムの実装例を示すのでこれらを見ながら再帰に慣れていきましょう。
暇な方は是非コードを写して実行してみたり、改造してみたりしてください。
フィボナッチ数列
再帰のとても有名な例としてフィボナッチ数列といった数列が挙げられます。
フィボナッチ数列のn項目は、次のような定義になっています。
数学的定義
F_n = \left\{
\begin{array}{ll}
0 & (n = 0) \\
1 & (n = 1) \\
F_{n-1} + F_{n-2} & (n \geq 2)
\end{array}
\right.
Javaによる実装
class Fibo {
public static void main(String[] args) {
System.out.println(fibo(10)); // 55
}
static int fibo(int n) {
if(n < 2) {
return n;
} else {
return fibo(n - 1) + fibo(n - 2);
}
}
}
階乗
一般的に階乗は 1, 2,..., n の積を求める関数ですが、以下のように再帰的に定義することも可能です。
数学的定義
f(n) = \left\{
\begin{array}{ll}
1 & (n = 0) \\
n * f(n - 1) & (n \geq 1)
\end{array}
\right.
Javaによる実装例
class Factorial {
public static void main(String[] args) {
System.out.println(factorial(10)); // 3628800
}
static int factorial(int n) {
if(n == 0) {
return 1;
} else {
return n * factorial(n - 1);
}
}
}
累乗
累乗も階乗と同様に再帰的に定義できます。ただし、指数は正の整数のみを取り扱います。
数学的定義
f(a, n) = a^n\\
f(a, n) = \left\{
\begin{array}{ll}
1 & (n = 0) \\
a * f(a, n - 1) & (n \geq 1)
\end{array}
\right.
Javaによる実装例
class Power {
public static void main(String[] args) {
System.out.println(power(2, 10)); // 1024
}
static int power(int a, int n) {
if(n == 0) {
return 1;
} else {
return a * power(a, n - 1);
}
}
}
累乗(高速化)
先ほどの累乗を計算する方法では、指数nに比例して計算回数が増えます。
そこで指数部を半分に分割することで高速化を図ります。
言葉で説明するのが難しいので下の定義、プログラムを参照してください。
数学的定義
f(a, n) = a^n\\
f(a, n) = \left\{
\begin{array}{ll}
1 & (n = 0) \\
f(a, n/2) * f(a, n / 2) & (n \geq 1)
\end{array}
\right.
Javaによる実装例
nが奇数の時には2で割ると余りが出てしまうため、n / 2の計算で切り捨てが発生してしまいます。
そこで、nが奇数の時は a * power(a, n / 2) * power(a, n / 2) とすることで調整します。
再帰関数全体での計算回数はnが0になるまで2で割った回数と等しいため、log2(n)回にすることができます。
また、power(a, n / 2)の計算結果をhalfPowerという変数に格納していることに注意してください。
これを行わずに power(a, n / 2) を2回呼び出すと計算回数はn回になってしまいます。
class Power {
public static void main(String[] args) {
System.out.println(power(2, 11)); //
}
static int power(int a, int n) {
if(n == 0) {
return 1;
}
int halfPower = power(a, n / 2);
if(n % 2 == 0) {
return halfPower * halfPower;
} else {
return a * halfPower * halfPower;
}
}
}
プログラムにおける関数の挙動
ここまでいくつかの再帰関数の定義と実装例を見てきましたが、プログラム上で定義された再帰関数は一体どのようにして実行されるのでしょう。
再帰関数は関数の特殊な例であるため、関数全般の挙動を理解するところから始めます。
それを理解するキーとなるのがスタック構造と呼ばれるコンピュータにおける関数と密接な関係にあるデータ構造です。
ここでは、スタック構造と関数の呼び出しに焦点を当てて学びます。
スタック構造
スタック構造には次のような2つの操作が存在します。
- push(x) : スタック領域に任意のデータxを追加する。xを積むとも言います。
- pop() : 最後に追加したデータを取り出す。
重要な点は最後に追加したものから取り出していく点です。
関数とスタック構造
スタック構造が関数にどのように関係しているのかを知るには次のコードを実行すると良いでしょう。
class StackTest {
public static void main(String[] args) {
System.out.println("Start: main()");
nextFunc(1);
System.out.println("End: main()");
return;
}
static void nextFunc(int a) {
System.out.println("Start: nextFunc(" + a + ")");
lastFunc(a + 1);
System.out.println("End: nextFunc(" + a + ")");
return;
}
static void lastFunc(int b) {
System.out.println("Start: lastFunc(" + b + ")");
System.out.println("End: lastFunc(" + b + ")");
return;
}
}
Start: main()
Start: nextFunc(1)
Start: lastFunc(2)
End: lastFunc(2)
End: nextFunc(1)
End: main()
関数の実行と終了の順番が以下の様になったことが確認できました。
- 実行順 :
main()->nextFunc(1)->lastFunc(2) - 終了順 :
lastFunc(2)->nextFunc(1)->main()
このような挙動になるためには、各関数がどこから呼び出されたか覚えている必要があります。
例えば、lastFunc(2)->nextFunc(1)と関数の処理が戻っていますが、これはlastFunc(2)が自分の呼び出し元はnextFunc(1)であるということを知っていなければいけません。
もっと厳密に言えば、nextFunc(1)の何行目で呼ばれたのかまで知っている必要があります。
そこでコンピュータの内部では、これを実現するためにスタック構造を利用しています。
具体的には次のような操作を行うことでこのような挙動が得られます。
- 現在ある関数
func()を実行している - その関数内で新たに別の関数
nextFunc()を呼び出そうとする - スタック領域に現在実行している
func()の情報を積む -
nextFunc()を実行し始める -
nextFunc()の実行が終わる - スタック領域から最後に追加された
func()の情報を読み出す -
func()内でnextFunc()を呼び出した場所から処理を再開
func()の情報を積むとありますが、これは以下の2つの情報を積んでいると考えてもらって問題ありません。
-
func()の処理が現在どこまで進んでいるのか -
func()内の変数の値(引数も(func()内の変数であると考えます)
また、コード内で明示的にreturnしていますが、大雑把に言うとreturn文は上の手順5-7に加えて戻り値を返すということをしてくれます(今回は戻り値がvoidなので何も返しません)。
つまり、関数の正しい呼び出し元に処理を戻すということを行ってくれます。
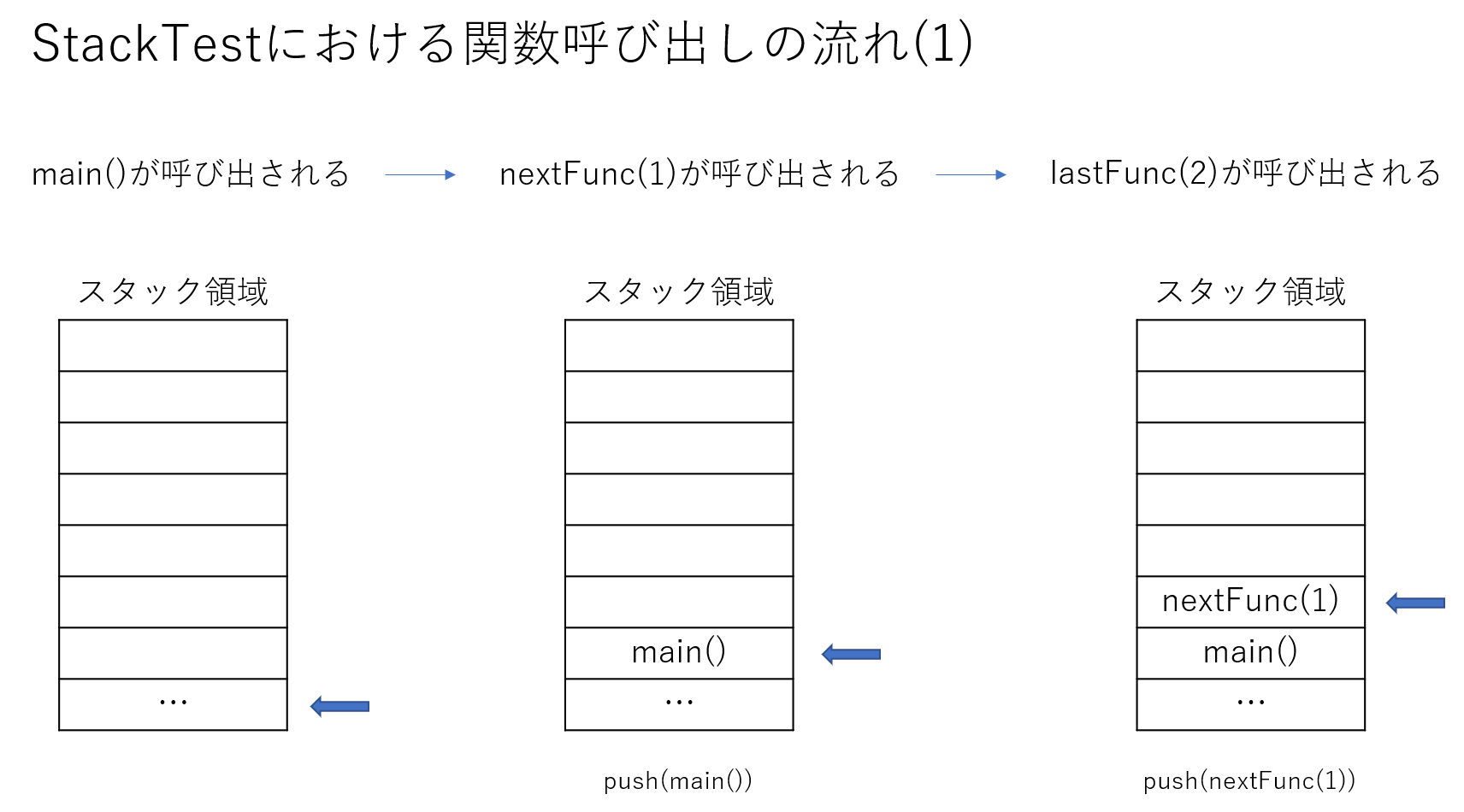
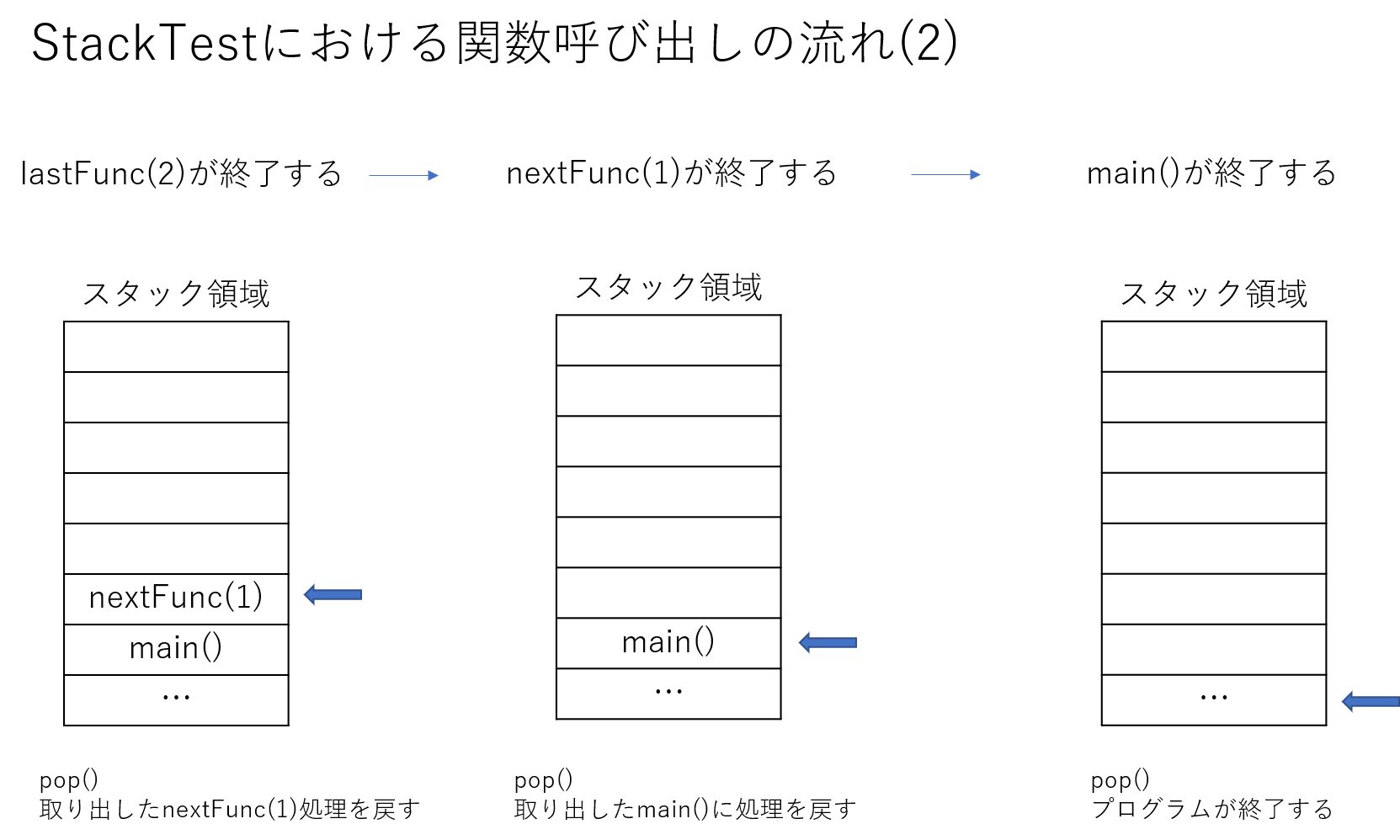
関数とスタック構造(イメージ図)
図で示すと次のようになります。
プログラムにおける再帰関数の挙動
関数の呼び出しがどのようになっているのか分かったところで再帰関数の挙動について見ていきましょう。
ここでは、分岐しない再帰と分岐する再帰に分けて説明します。
特にこういった分け方がよくされるわけではありませんが、私はいつもこの2つについて考えています。
なぜこの2つに分けるのかは、後々説明いたします。
分岐しない再帰
私は次のようなものを分岐しない再帰と呼んでいます。
- 再帰関数内で再帰呼び出しを1回しか行わない。
例として、先程紹介した階乗が挙げられます。もう一度階乗の定義を確認しましょう。
階乗の定義(確認)
f(n) = \left\{
\begin{array}{ll}
1 & (n = 0) \\
n * f(n - 1) & (n \geq 1)
\end{array}
\right.
上の定義から、確かに再帰呼び出しは一回しか行われないことがわかると思います。
したがって、階乗は分岐しない再帰であると言えます。
再帰の挙動
ここで、分岐しない再帰の挙動がどうなるか次のプログラムを実行して確認してみましょう。
class PowerCheck {
public static void main(String[] args) {
System.out.println("power(5) = " + power(5)); // 120
}
static int power(int n) {
System.out.println("power(" + n + ")");
if(n == 0) {
return 1;
} else {
return n * power(n - 1);
}
}
}
power(5)
power(4)
power(3)
power(2)
power(1)
power(0)
power(5) = 120
power(5), power(4), ..., power(0)と順に再帰呼び出しが行われていることを確認できました。
分岐しない再帰は、このように線形方向に関数を呼び出すため、非常に簡単です。
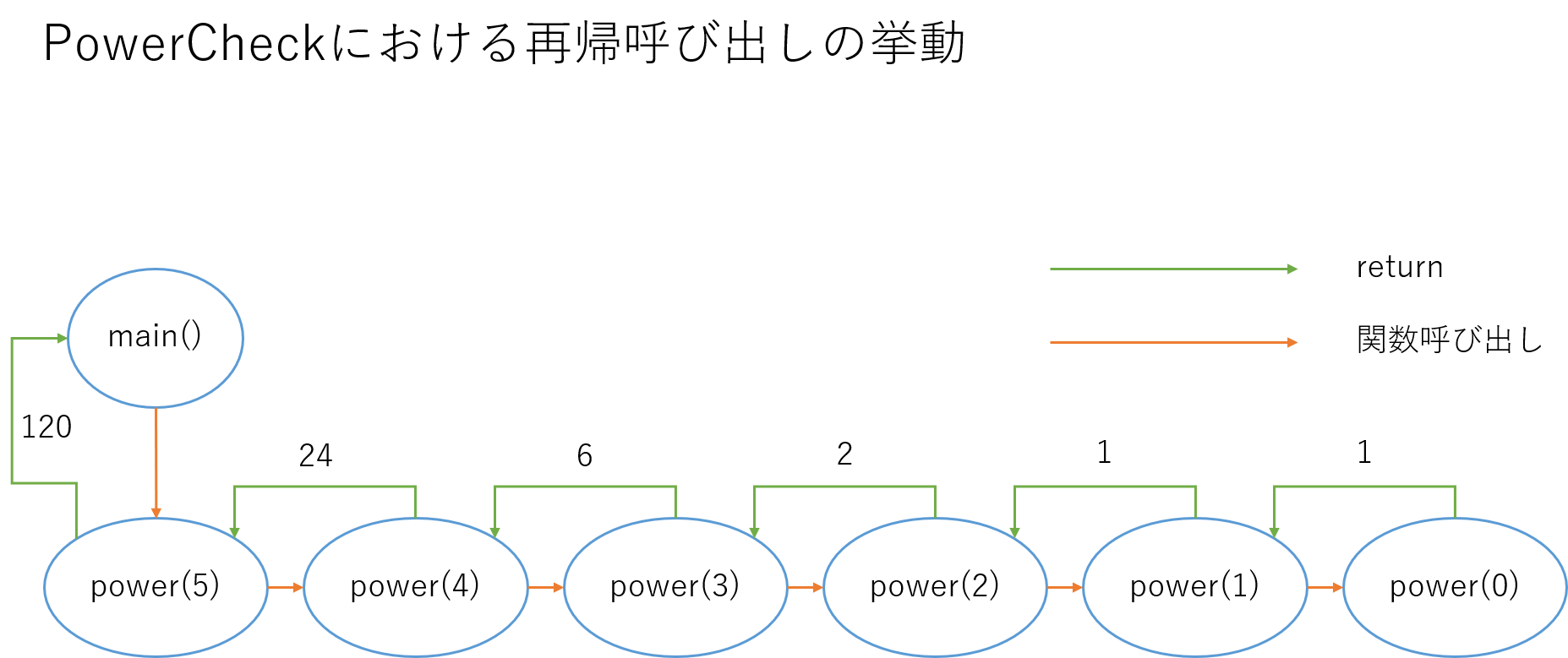
イメージ図
イメージ図は次のようになります。
分岐する再帰
私は、次のようなものを分岐する再帰と呼んでいます。
- 再帰関数内で異なる再帰呼び出しを2回以上行う。
例として、先程紹介したフィボナッチ数列がこれに当たります。もう一度階乗の定義を確認しましょう。
フィボナッチ数列の定義(確認)
F_n = \left\{
\begin{array}{ll}
0 & (n = 0) \\
1 & (n = 1) \\
F_{n-1} + F_{n-2} & (n \geq 2)
\end{array}
\right.
nが2以上のときに異なる再帰呼び出しを2回行うことがわかります。
したがって、フィボナッチ数列は分岐する再帰であると言えます。
分岐する再帰の挙動
ここで、分岐しない再帰の挙動がどうなるか次のプログラムを実行して確認してみましょう。
class FiboCheck {
public static void main(String[] args) {
System.out.println("fibo(5) = " + fibo(5)); // 5
}
static int fibo(int n) {
System.out.println("fibo(" + n + ")");
if(n < 2) {
return n;
} else {
return fibo(n - 1) + fibo(n - 2);
}
}
}
fibo(5)
fibo(4)
fibo(3)
fibo(2)
fibo(1)
fibo(0)
fibo(1)
fibo(2)
fibo(1)
fibo(0)
fibo(3)
fibo(2)
fibo(1)
fibo(0)
fibo(1)
fibo(5) = 5
分岐しない再帰のときに比べて、かなり複雑になりました。
これは、分岐する再帰では、関数呼び出しの順が線形方向ではないためです。
このようになる理由は、再帰呼出しが次のように行われているからです。
return fibo(n - 1) + fibo(n - 2);
ここは、初心者の方がとても詰まりやすい点です。
fibo(n - 1)→fibo(n - 2)の順で呼び出されるため、fibo(n - 2)はfibo(n - 1)内で値がreturnされて処理が終了されるまでは実行されません。
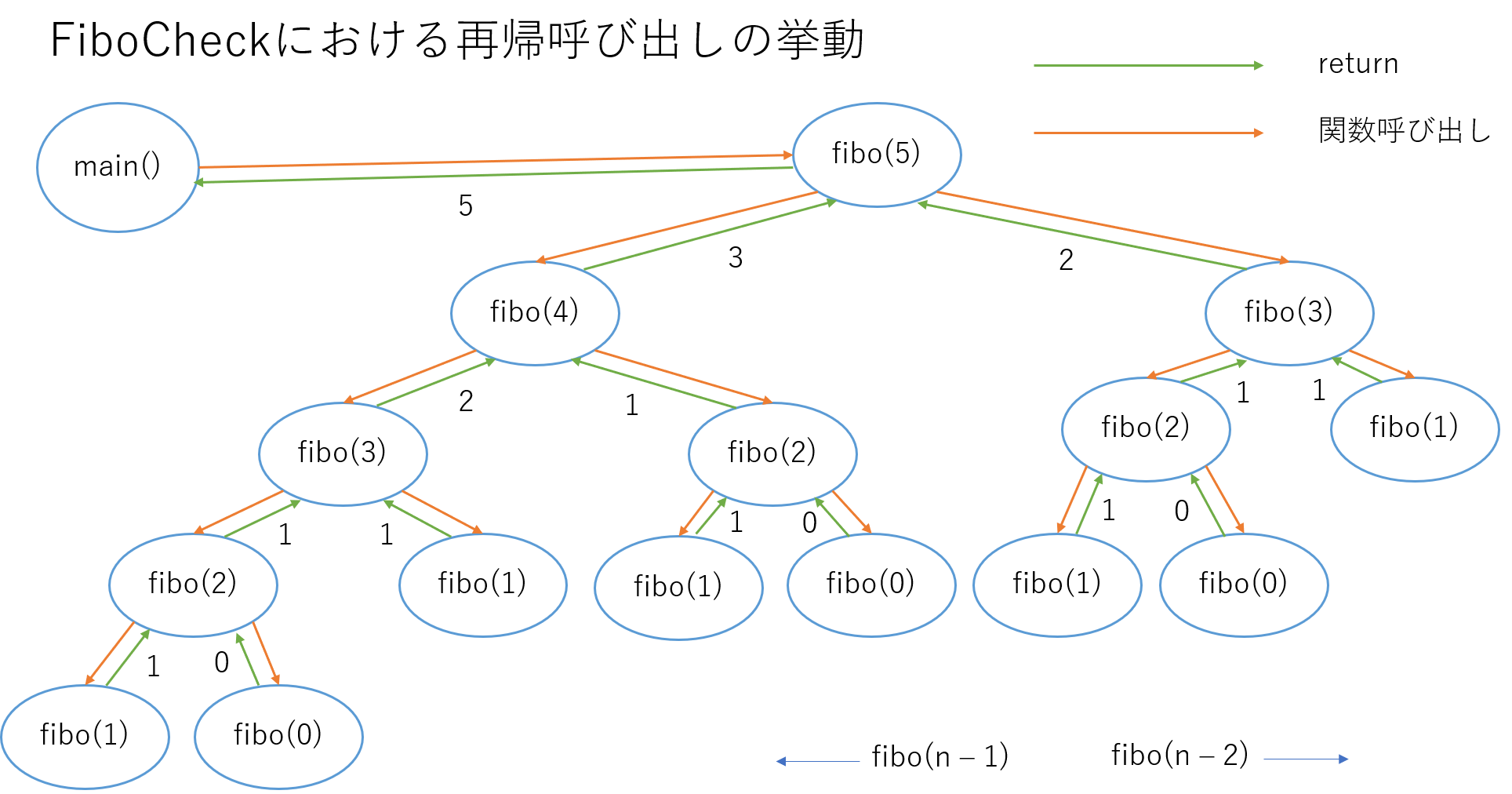
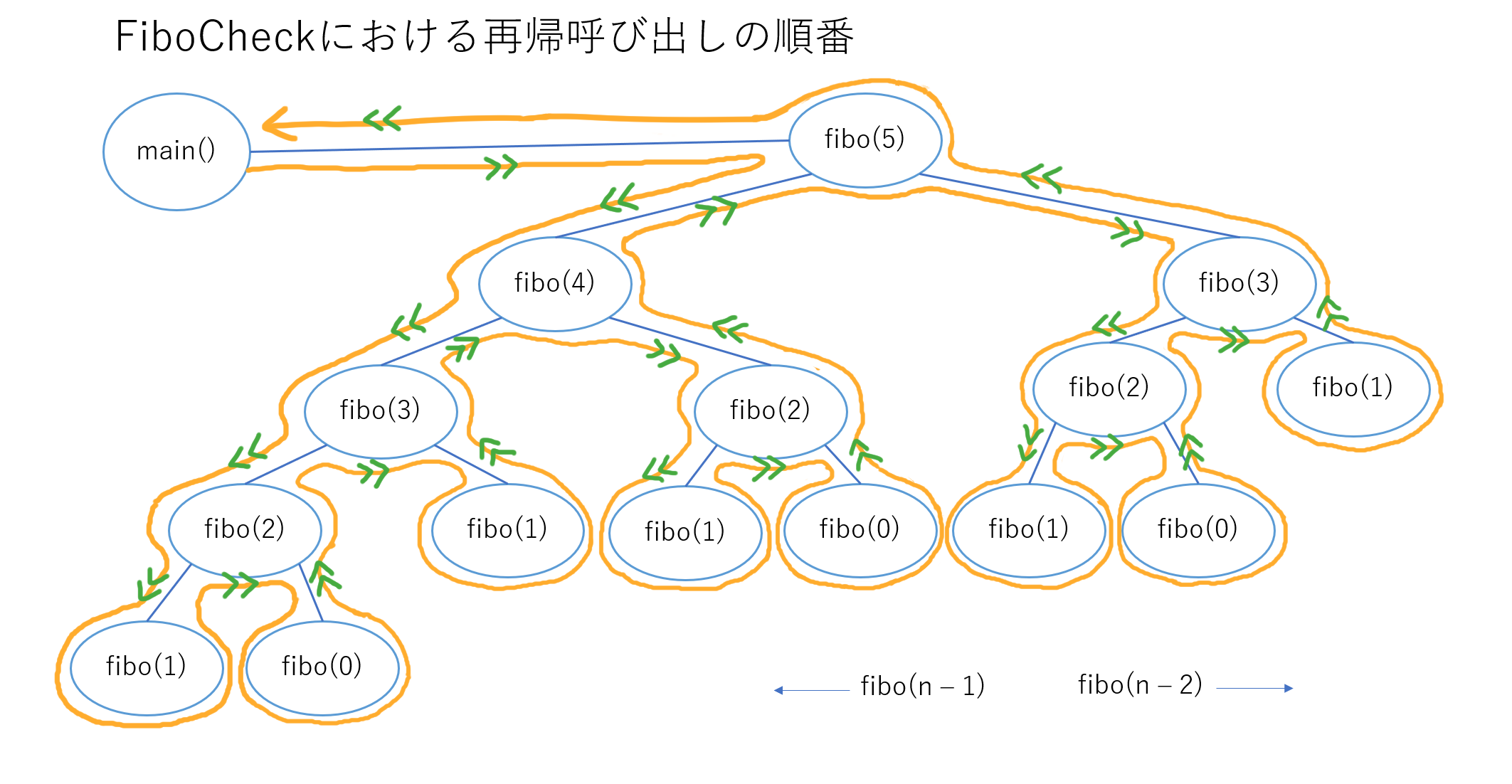
イメージ図
イメージ図は次のようになります。
nが2以上のときには、fibo(n - 1)とfibo(n - 2)が呼び出されるため、分岐が起こります。
nが0または1のときは、return nをしてそれ以上再帰呼び出しを行わないため、図で見ると最下層になることがわかります。
先程の、fibo(n - 1)→fibo(n - 2)の順で呼び出されるということから、呼び出しの流れを矢印で表すと次のような図になります。
例外もありますが、基本的に関数は、コードに書いた順に呼び出されます。
例えば、次のように再帰呼び出しの部分を書き換えれば、上の図のfibo(5)からの矢印は全て反対方向になります。
return fibo(n - 2) + fibo(n - 1);
分岐する再帰と分岐しない再帰の違い
階乗とフィボナッチ数列の例を通して、分岐する再帰と分岐しない再帰の挙動について見てきました。
これらの決定的な違いは一体なんでしょうか。それはずばり計算量です。
計算量
累乗のプログラムを高速化する際にも少し計算量の話が出てきました。
プログラムを書く際には、常に計算量を意識して書く必要があります。
計算量を考える際には大きく分けて以下の2つがあります。
- 時間計算量(実行時間に関わる計算量)
- 空間計算量(メモリ使用量に関わる計算量)
これらを表すのにオーダー記法といったものを利用します。
詳しくは、asksaitoさんの記事を見るとわかりやすく解説されています。
例えば、階乗のプログラムではnに対してn回の処理(再帰呼び出し)が行われました。
これは次のようにして表記します。
O(n)
では、フィボナッチ数列のn項目を計算するのにかかる計算量はどうでしょうか。
n = 0, 1の場合を除いてfibo(n) = fibo(n - 1) + fibo(n - 2)です。
大体の場合、再帰呼び出しを2回行うため、2分岐します(先程の図からもわかります)
したがって、計算量は多く見積もって下のようになります。
O(2^n)
これは致命的です。なぜなら、nの数が大きくなれば計算量が爆発的に増加してしまうからです。
試しに、フィボナッチ数列を求めるプログラムでn = 100として実行してみてください。多分一生終わりません。
しかし、再帰関数は、ある条件を満たす時、高速化することができます。
再帰関数の高速化
フィボナッチ数列の例を通して再帰関数の高速化について説明します。
メモ化再帰
次の条件が成り立つ時、メモ化再帰といった手法が利用できます。
-
f(x1, x2, ..., xn)は分岐する再帰関数である。 -
f(x1, x2, ..., xn)は(x1, x2, ..., xn)について値が一意に定まる。
フィボナッチ数列はどうでしょうか。
fibo(n)はどんなときでも一意に定まります。
あるタイミングでfibo(5)を呼び出したときと違うタイミングでfibo(5)を呼び出した時で値が変わりません。
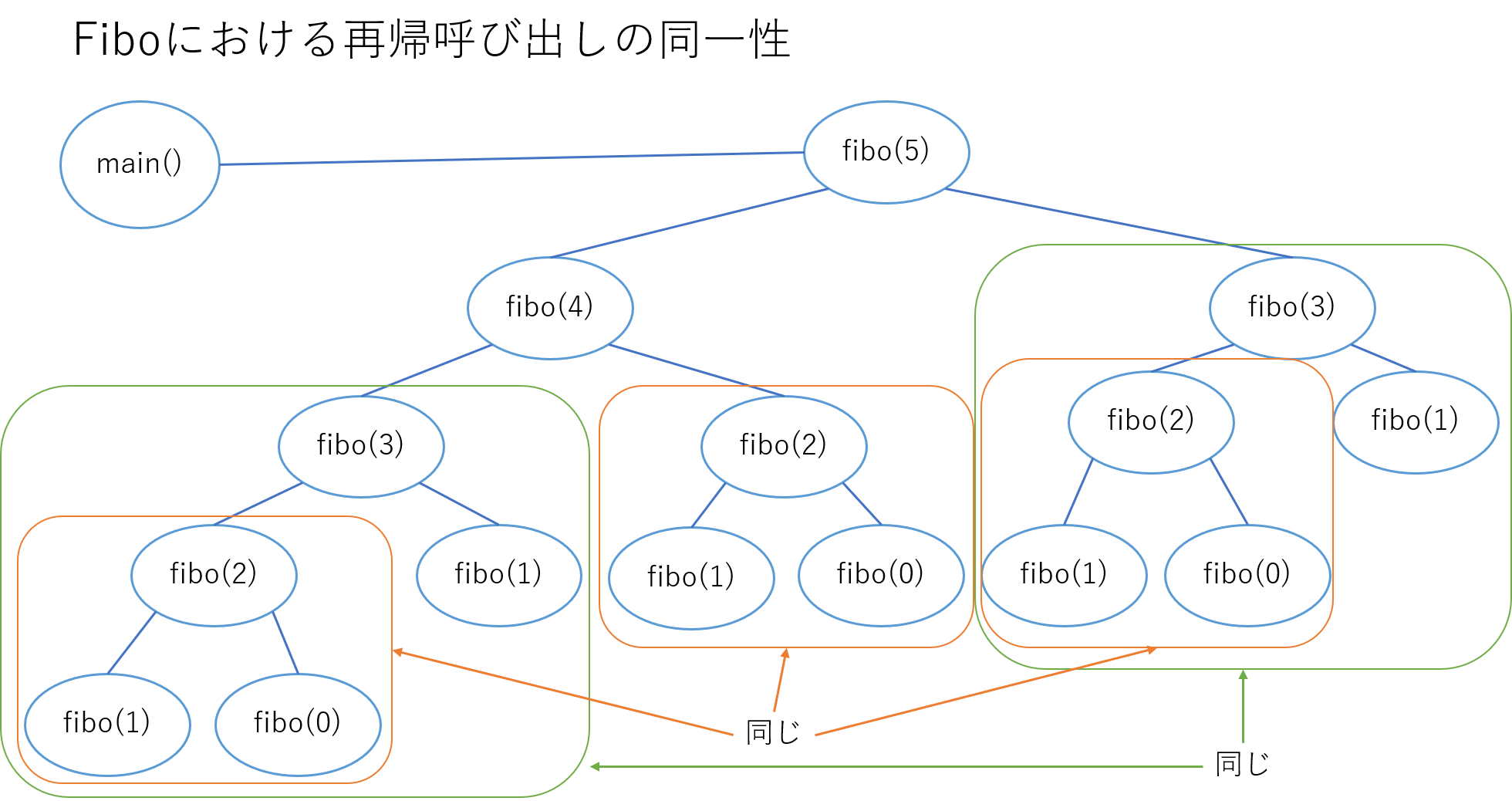
つまり、fibo(n)の値は他のどんな値よりもnに完全に従属しています。
また、下の図を見てもわかるように、fibo(2)やfibo(3)は既に一回計算しているにも関わらず、再計算しています。
このような時、メモ化再帰を利用して高速化することができます。
下がフィボナッチ数列をメモ化再帰を利用して求めるプログラムになります。
フィボナッチ数列を求めるプログラム(メモ化再帰)
class MemoFibo {
static final int MAX_FIBO = 50;
static long[] memo = new long[MAX_FIBO + 1];
public static void main(String[] args) {
for(int i = 0; i < memo.length; ++i) {
memo[i] = -1;
}
System.out.println("fibo(50) = " + fibo(50));
}
static long fibo(int n) {
if(memo[n] != -1L) {
return memo[n];
}
if(n < 2) {
memo[n] = n;
} else {
memo[n] = fibo(n - 1) + fibo(n - 2);
}
return memo[n];
}
}
fibo(50) = 12586269025
基本的にやっていることは簡単です。
関数の値(戻り値)を保存しておくための配列を用意し、あるnについてfibo(n)を計算したらそれを配列に保存します。
そして、また同じnについてfibo(n)を計算しようとした際に値を再利用します。
これによって、fibo(n)は各nについて一度しか呼び出されないため、計算量は以下のようになります。
- 時間計算量: O(n)
- 空間計算量: O(n)
メモリを利用して指数時間から線形時間まで時間計算量を落とすことができました。
これによってnが大きくなってもメモリが許す範囲で現実的な時間内に計算することができます。
また、今回は引数がint nの1つしかありませんが、これが複数個(x1, x2, ..., xn)あった場合でも、メモ配列をn次元配列に拡張することでメモ化再帰を適用することができます。
使い所
メモ化再帰は、今回のように同じ引数で関数が何回も呼び出されるときに有効です。
しかし、分岐しない再帰には、メモ化再帰は適用できないことに注意してください。
これは、線形的な再帰呼び出しでは、引数がそもそも被ることがないからです。
この性質を理解せずに無闇にメモ化を行うと意味もなくメモリを無駄遣いしてしまう酷いプログラムになってしまいます。
スタックオーバーフロー対策
スタックオーバーフロー
Javaでは再帰をしすぎると以下のような例外が発生します。
再帰とスタックオーバーフローは切っても切れない関係です。
Exception in thread "main" java.lang.StackOverflowError
これは、関数を呼び出しすぎたことでスタック領域が満たんになってしまうことが原因です。
これを解決するためには、2つの方法があります。
- 末尾再帰を使う
- そもそも再帰ではなくループ処理を使う
末尾再帰
次の条件が成り立つ時、末尾再帰といった手法が利用できます。
-
f(x1, x2, ..., xn)は分岐しない再帰関数である。 -
f(x1, x2, ..., xn)内の最後の処理が自身の再帰呼び出しのみである。
例えば、0からnまでの整数の和は次のように定義できます(公式を使えば一回の計算で求められますが今回はしません)。
sigma(n) = \sum_{i=0}^n i\\
sigma(n) = \left\{
\begin{array}{ll}
0 & (n = 0) \\
n + sigma(n - 1) & (n \geq 1)
\end{array}
\right.
\\
これを再帰関数を用いてプログラムを書くと下のようになります。
実装例(一般的な再帰)
public class Sigma {
public static void main(String[] args) {
System.out.println("sigma(1000000) = " + sigma(1000000)); // StackOverflowError
}
static long sigma(int n) {
if(n == 0) {
return 0;
} else {
return n + sigma(n - 1);
}
}
}
上のコードでは、return n + sigma(n - 1)となっており、最後の処理が自身の再帰呼び出しになっていません。
見た目上はsigma(n - 1)が最後に実行されている様に見えますが、+演算子によってnとsigma(n - 1)を加算するといった処理が走っています。
これを末尾再帰が行えるように書き換えます。
目標は、return文の後ろを再帰呼び出しだけの状態にすることです。
書き換えたコードが下になります。
実装例(末尾再帰)
public class SigmaTailCall {
public static void main(String[] args) {
System.out.println("sigma(1000000) = " + sigma(1000000)); // StackOverflowError
}
static long sigma(int n) {
return sigma(n, 0);
}
static long sigma(int n, long sum) {
if(n == 0) {
return sum;
} else {
return sigma(n - 1, sum + n);
}
}
}
上のコードに改造したことで改造前は、計算結果を関数自体が値(戻り値)として保持していたのが、引数の変数によって保持するようになりました。
これによって、return文の後ろが再帰呼び出しだけの状態になりました。
処理を見てみると、この関数はnとsumの値を変化させながら線形方向に手続きを実行しているだけであることがわかります。
したがって、この関数は本質的にはループ処理と同じであると言えます。
ループであるなら関数をスタック領域に積む必要もなく、スタックオーバーフローは起こらないはずです。
このような末尾再帰の形にすることによって、コンパイラが自動的に最適化してくれます。
めでたしめでたし。
と言いたいところですが、Javaは末尾再帰の最適化を行ってくれません
実際に、上の末尾再帰化したプログラムを実行してもスタックオーバーフローが発生します。
ループへの手動変換
幸いなことに末尾再帰はループ処理と相互変換ができます。
Wikipedia - 末尾再帰より、次のように変換をすることができます。
public class LoopSigma {
public static void main(String[] args) {
System.out.println("sigma(1000000) = " + sigma(1000000)); // 500000500000
}
static long sigma(int n) {
return sigma(n, 0);
}
static long sigma(int n, long sum) {
while(true) {
if(n == 0) {
return sum;
}
sum = sum + n;
n = n - 1;
}
}
}
sigma(10000000) = 500000500000
再帰を使わないのは本末転倒な気もしますが、無事にスタックオーバーフローを回避することができました。
重要なのは、末尾再帰は簡単にループ処理に変換できるという点です。
再帰と分割統治法
分割統治法
分割統治法とは、ある大きな問題を小さな問題に分割し、それらを全て解くことによって分割前の問題を解く手法です。
この説明を聞いて勘の良い方は既にお気づきだと思います。
これまで、フィボナッチ、階乗、累乗、0からnまでの和を再帰的に求めてきましたが、これらは全て分割統治法だったのです。
分割統治法と再帰は非常に相性が良く、優れたアルゴリズムは再帰的である場合が多いです。
有名な例としては、二分探索や深さ優先探索、クイックソート、マージソート等が挙げられます。
今回は、再帰を使ってかつ理解しやすいクイックソートを取り上げます。
クイックソート
クイックソートは分割統治法を用いた非常に有名なソートアルゴリズムです。
- ソート区間の中から一つデータを選択する(ピボット)
- ピボット以下のデータを前方に移動させ、ピボット以上のデータを後方に寄せる。
- ピボットを境界として二分割したデータをそれぞれソートする
上の操作を再帰的に行うことで全てのデータをソートすることができます。
public class QuickSort {
public static void main(String[] args) {
final int DATA_NUM = 10;
int[] data = new int[DATA_NUM];
Random rnd = new Random();
for(int i = 0; i < data.length; ++i) {
data[i] = rnd.nextInt(100);
}
printArray(data);
quickSort(data, 0, data.length - 1);
printArray(data);
}
static void quickSort(int[] data, int left, int right) {
if(left >= right) {
return;
}
int l = left;
int r = right;
int pivot = data[l + (r - l) / 2];
int temp;
while(l <= r) {
while(data[l] < pivot) {
++l;
}
while(data[r] > pivot) {
--r;
}
if(l <= r) {
temp = data[l];
data[l] = data[r];
data[r] = temp;
++l;
--r;
}
}
quickSort(data, left, r);
quickSort(data, l, right);
}
static void printArray(int[] data) {
System.out.print(data[0]);
for(int i = 1; i < data.length; ++i) {
System.out.print(", " + data[i]);
}
System.out.println();
}
}
ギフト
トコロテンサンタ🎅からギフトを授けます。以下のプログラムを実行してください。
public class Gift {
public static void main(String[] args) {
int d = 2;
char[][] label = {
{ ' ', ' ', ' ', '#', '#', '#', ' ', ' ', ' ', ' ', ' ', ' ' },
{ ' ', '#', '#', ' ', ' ', ' ', '#', '#', ' ', ' ', ' ', ' ' },
{ ' ', '#', ' ', ' ', ' ', ' ', ' ', ' ', '#', ' ', ' ', ' ' },
{ ' ', '#', ' ', ' ', ' ', ' ', ' ', ' ', ' ', '#', ' ', ' ' },
{ ' ', '#', ' ', ' ', ' ', ' ', ' ', ' ', ' ', '#', '#', ' ' },
{ ' ', '#', '#', ' ', ' ', ' ', ' ', ' ', ' ', ' ', '#', '#' },
{ ' ', ' ', '#', '#', ' ', ' ', ' ', ' ', ' ', ' ', ' ', '#' },
{ ' ', ' ', ' ', '#', '#', '#', ' ', ' ', ' ', ' ', ' ', '#' },
{ ' ', ' ', ' ', ' ', ' ', '#', '#', '#', '#', ' ', ' ', '#' },
{ ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', '#', '#', '#', '#' }
};
char[][] pattern = {
{ '#', '#', '#', '#', '#', '#', '#' },
{ '#', ' ', ' ', '#', ' ', ' ', '#' },
{ '#', '#', '#', '#', '#', '#', '#' },
{ '#', ' ', ' ', '#', ' ', ' ', '#' },
{ '#', '#', '#', '#', '#', '#', '#' }
};
String secretMessage = "Mfrsy!Cirjsumbs/";
printLabel(label, pattern, d);
printPattern(pattern, d);
printSecretMessage(secretMessage);
}
static int power(int a, int n) {
if(n == 0) {
return 1;
} else {
return a * power(a, n - 1);
}
}
static void printLabel(char[][] label, char[][] pattern, int d) {
int patternWidth = power(pattern[0].length, d);
for(int y = 0; y < label.length; ++y) {
for(int x = 0; x < (patternWidth - label[0].length * 2) / 2; ++x) {
System.out.print(" ");
}
for(int x = 0; x < label[0].length; ++x) {
System.out.print(label[y][x]);
}
for(int x = label[0].length - 1; x >= 0; --x) {
System.out.print(label[y][x]);
}
System.out.println();
}
}
static boolean existCharacter(char[][] pattern, int d, int x, int y) {
if(d == 1) {
return pattern[y][x] == '#';
} else {
return existCharacter(pattern, d - 1, x / pattern[0].length, y / pattern.length);
}
}
static void printPattern(char[][] pattern, int d) {
int patternWidth = power(pattern[0].length, d);
int patternHeight = power(pattern.length, d);
for(int y = 0; y < patternHeight; ++y) {
for(int x = 0; x < patternWidth; ++x) {
if(existCharacter(pattern, d, x, y)) {
System.out.print(pattern[y % pattern.length][x % pattern[0].length]);
} else {
System.out.print(' ');
}
}
System.out.println();
}
}
static void printSecretMessage(String secretMessage) {
for(int i = 0; i < secretMessage.length(); ++i) {
System.out.print((char)(secretMessage.charAt(i) - i % 2));
}
System.out.println();
}
}
最後に
冬休みに再帰をたくさん書いて**†圧倒的成長†**を遂げましょう。
実はもっと書きたいことがありましたが、アドベントカレンダーに間に合わなくなってしまいそうだったので今回はここまでとしました。
最後まで読んでくださった方(多分いない)、ありがとうございました。