はじめに
Linear Cryptanalysis(線形解読法)を説明します。[1]を解説します。
The Basic SPN Cipher
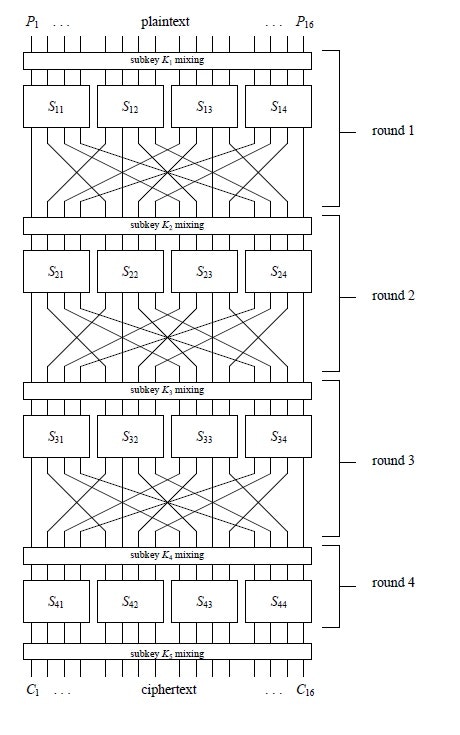
例として使用する Substitution-Permutation Network (SPN) Cipher の図を示します。
plaintext / ciphertext の bit length は 16bitです。roundは4です。
plaintextをP1,...,P16と表記します。ciphertextをC1,...,C16と表記します。
round i に対する key を Ki,1 ... Ki,16 と表記します。
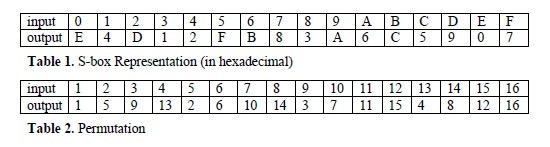
Substitutionは4bit 符号なし整数の置換です。置換表をS-Boxといいます。
round i に対する S-Box を $S_{i1},S_{i2},S_{i3},S_{i4}$ と表します。すべて同じS-Boxです。
Permutation は 16bit をまとまりとした bit の並び替えです。それぞれ、具体的には以下の通りです。
具体的な実装例はCode Example [C1] を参照ください。
S-Box に対する Linear Approximation
S-Box に対する Linear Approximationを考えます。
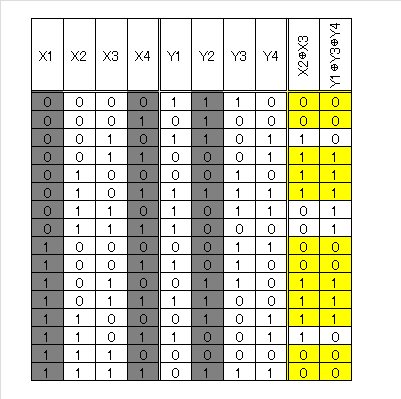
S-Box のinput / output は4bitです。X1, Y1がMSBです。
次の式が成り立つ確率を考えます。
$\oplus$は排他的論理和(XOR)です。$\bullet$は論理積(AND)です。式1とします。
a_1 \bullet X_1 \oplus a_2 \bullet X_2 \oplus a_3 \bullet X_3 \oplus a_4 \bullet X_4 = b_1 \bullet Y_1 \oplus b_2 \bullet Y_2 \oplus b_3 \bullet Y_3 \oplus b_4 \bullet Y_4 \\
X_i, Y_i, a_i, b_i \in \{0, 1\} \\
a, bの例として a1a2a3a4 = 0110b = 0x6, b1b2b3b4 = 1011b = 0xB を考えます。
式1は次のようになります。
X_2 \oplus X_3 = Y_1 \oplus Y_3 \oplus Y_4
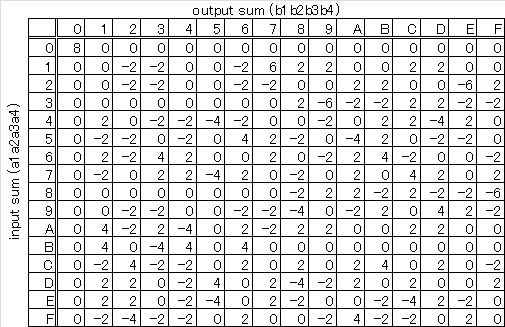
すべての input / output に対して式が成立する回数をカウントします。
次に示す通り12通りとなります。
すべての a, b に対して上記を実行した結果を次に示します。
理想的な式1の成立回数は8です。
8からの偏りを明確にするため、式1の成立回数を"-8"した回数をセルの値とします。
したがって、[セルの値] / 16 が 頻度の偏り(以降、biasといいます)になります。
具体的な実装例はCode Example [C2] を参照ください。
The Basic SPN Cipher に対する Linear Approximation
S-Box に対する Linear Approximationを使って
The Basic SPN Cipher に対する Linear Approximationを構成します。
構成方法はさまざま考えられますが、
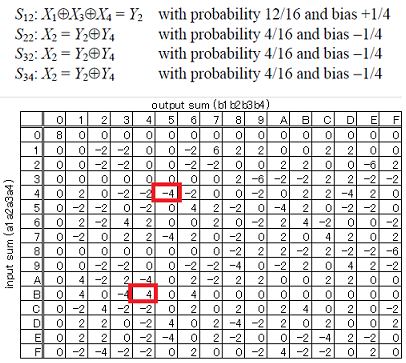
ここでは例として、各S-Boxに対して、次のLinear Approximationを考えます。
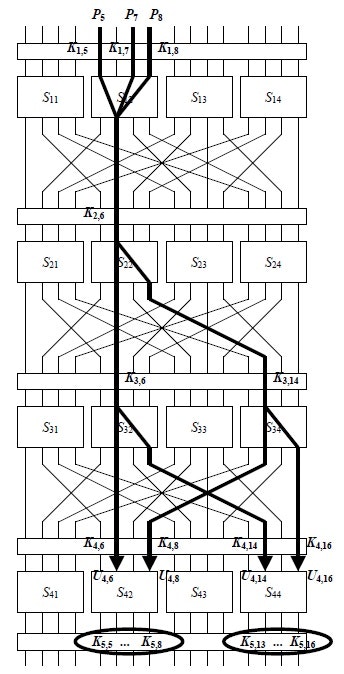
上記をCipher全体に適用します。注目しているbitのデータフローを太線で示します。
round i に対する S-Box の 入力をUi,1 ... Ui,16と表記します。出力をVi,1 ... Vi,16と表記します。
S12について以下を考えます。
U_{1,5} \oplus U_{1,7} \oplus U_{1,8} = V_{1,6} \\
上記はplaintextとkeyを使って次のように表せます。式2とします。
P_5 \oplus K_{1,5} \oplus P_7 \oplus K_{1,7} \oplus P_8 \oplus K_{1,8} = V_{1,6} \\
S22について以下を考えます。
U_{2,6} = V_{2,6} \oplus V_{2,8} \\
上記は式2とkeyを使って次のように表せます。式3とします。
V_{1,6} \oplus K_{2,6} = V_{2,6} \oplus V_{2,8} \\
P_5 \oplus K_{1,5} \oplus P_7 \oplus K_{1,7} \oplus P_8 \oplus K_{1,8} \oplus K_{2,6} = V_{2,6} \oplus V_{2,8} \\
S32,S34について以下を考えます。
U_{3,6} = V_{3,6} \oplus V_{3,8} \\
U_{3,14} = V_{3,14} \oplus V_{3,16} \\
上記から以下が成り立ちます。
U_{3,6} \oplus U_{3,14} = V_{3,6} \oplus V_{3,8} \oplus V_{3,14} \oplus V_{3,16} \\
上記は式3とkeyを使って次のように表せます。式4とします。
P_5 \oplus K_{1,5} \oplus P_7 \oplus K_{1,7} \oplus P_8 \oplus K_{1,8} \oplus K_{2,6} \oplus K_{3,6} \oplus K_{3,16} = V_{3,6} \oplus V_{3,8} \oplus V_{3,14} \oplus V_{3,16} \\
P_5 \oplus P_7 \oplus P_8 \oplus K_{1,5} \oplus K_{1,7} \oplus K_{1,8} \oplus K_{2,6} \oplus K_{3,6} \oplus K_{3,16} = V_{3,6} \oplus V_{3,8} \oplus V_{3,14} \oplus V_{3,16} \\
S42,S44の入力について式4とkeyを使って次のように表せます。式5とします。
U_{4,6} \oplus U_{4,8} \oplus U_{4,14} \oplus U_{4,16} = V_{3,6} \oplus V_{3,8} \oplus V_{3,14} \oplus V_{3,16} \oplus K_{4,6} \oplus K_{4,8} \oplus K_{4,14} \oplus K_{4,16} \\
U_{4,6} \oplus U_{4,8} \oplus U_{4,14} \oplus U_{4,16} = P_5 \oplus P_7 \oplus P_8 \oplus K \\
U_{4,6} \oplus U_{4,8} \oplus U_{4,14} \oplus U_{4,16} \oplus P_5 \oplus P_7 \oplus P_8 = K \\
Kは次の通りです。Kは暗号化を通じて変化しないため 0 or 1 固定となります。
K = K_{1,5} \oplus K_{1,7} \oplus K_{1,8} \oplus K_{2,6} \oplus K_{3,6} \oplus K_{3,16} \oplus K_{4,6} \oplus K_{4,8} \oplus K_{4,14} \oplus K_{4,16} \\
次に式5が成立する確率を計算します。次の式で計算できます。Piling-Up Lemmaといいます。
\frac{1}{2} + 2^{n-1} ( \varepsilon_1 + ... + \varepsilon_n ) \\
$\varepsilon_n$ は S-Box に対する Linear Approximation によって得られるbiasです。
式5が (成立する or 成立しない) 確率は次の通り計算できます。S12,S22,S32,S34のbiasを使います。
成立するかどうかはKに依存します。Kは未知であるため決定できません。
\frac{1}{2} + 2^3 (\frac{1}{4})(- \frac{1}{4})(- \frac{1}{4})(- \frac{1}{4}) = \frac{1}{2} - \frac{1}{32} = \frac{15}{32}
したがって式5が成立する , 成立しない確率は それぞれ $\frac{15}{32}$ , $\frac{17}{32}$ になります。
いずれもbiasは $\frac{1}{32}$となります。
Keyの導出
いままでの結果をまとめます。
次の式が成立するbiasは$\frac{1}{32}$です。式6とします。
U_{4,6} \oplus U_{4,8} \oplus U_{4,14} \oplus U_{4,16} \oplus P_5 \oplus P_7 \oplus P_8 = 0 \\
上記を計算するには U4,6 U4,8 U4,14 U4,16 が未知です。
これは既知である C5~C8,C13~C16 に対して
K5,5~K5,8 K5,13~K5,16 (16bit) すべてのパターンで CとのXORとS-Boxの逆対応をすることで得られます。
多数の plaintext / ciphertext に対して 式6の成立確率を計算します。
biasが$\frac{1}{32}$に近くなるKeyが正しいKeyであると判断できます。
具体的な実装例はCode Example [C3] を参照ください。
正しいKey 0x9A の成立回数が一番多くなっています。
Code Example
Code Exampleを記載します。
CFLAGS=-I. -Wall -Werror -O2
INCS=
OBJS=test.o
LIBS=
TARGET=test
%.o: %.c $(INCS)
$(CC) $(CFLAGS) -c -o $@ $<
$(TARGET): $(OBJS)
$(CC) $(CFLAGS) -o $@ $^ $(LIBS)
clean:
rm -rf $(TARGET) *.o
[C1] Basic SPN Cipher
# include <stdio.h>
# include <stdint.h>
# include <stdbool.h>
# include <string.h>
//0x0, 0x1, 0x2, 0x3, 0x4, 0x5, 0x6, 0x7, 0x8, 0x9, 0xA, 0xB, 0xC, 0xD, 0xE, 0xF,
static const uint8_t Sbox[] = { 0xE, 0x4, 0xD, 0x1, 0x2, 0xF, 0xB, 0x8, 0x3, 0xA, 0x6, 0xC, 0x5, 0x9, 0x0, 0x7, };
static const uint8_t InvSbox[] = { 0xE, 0x3, 0x4, 0x8, 0x1, 0xC, 0xA, 0xF, 0x7, 0xD, 0x9, 0x6, 0xB, 0x2, 0x0, 0x5, };
static const uint8_t Key[] = { 0x0, 0x1, 0x2, 0x3, 0x4, 0x5, 0x6, 0x7, 0x8, 0x9, }; // 5 x 16bit = 5 x 2byte = 10byte
static const int round = 4;
static void print(const char* header, const char* footer, uint8_t* buf, int size)
{
int i;
printf("%s", header);
for (i=0; i<size; i++) {
printf("%02X ", buf[i]);
}
printf("%s", footer);
}
static void Substitution(uint8_t* S, bool is_inv)
{
uint8_t* box, _S[2];
if (is_inv) {
box = (uint8_t*)InvSbox;
} else {
box = (uint8_t*)Sbox;
}
_S[0] = box[S[0]&0x0F];
_S[0] |= (box[S[0]>>4]<<4);
_S[1] = box[S[1]&0x0F];
_S[1] |= (box[S[1]>>4]<<4);
memcpy(S, _S, 2);
}
static void Permutation(uint8_t* S)
{
uint8_t tmp[2];
/* bit0 */
tmp[0] = (S[0] & 0x80);
tmp[0] |= (S[0] & 0x08)<<3;
tmp[0] |= (S[1] & 0x80)>>2;
tmp[0] |= (S[1] & 0x08)<<1;
/* bit1 */
tmp[0] |= (S[0] & 0x40)>>3;
tmp[0] |= (S[0] & 0x04);
tmp[0] |= (S[1] & 0x40)>>5;
tmp[0] |= (S[1] & 0x04)>>2;
/* bit2 */
tmp[1] = (S[0] & 0x20)<<2;
tmp[1] |= (S[0] & 0x02)<<5;
tmp[1] |= (S[1] & 0x20);
tmp[1] |= (S[1] & 0x02)<<3;
/* bit3 */
tmp[1] |= (S[0] & 0x10)>>1;
tmp[1] |= (S[0] & 0x01)<<2;
tmp[1] |= (S[1] & 0x10)>>3;
tmp[1] |= (S[1] & 0x01);
memcpy(S, tmp, 2);
}
static void cipher(const uint8_t* P, uint8_t* C)
{
int i; bool inv = false;
uint8_t S[2];
memcpy(S, P, 2);
for (i=0; i<round-1; i++) {
S[0] ^= Key[i*2+0]; S[1] ^= Key[i*2+1];
Substitution(S, inv);
Permutation(S);
}
S[0] ^= Key[6]; S[1] ^= Key[7];
Substitution(S, inv);
S[0] ^= Key[8]; S[1] ^= Key[9];
memcpy(C, S, 2);
}
static void inv_cipher(const uint8_t* C, uint8_t* P)
{
int i; bool inv = true;
uint8_t S[2];
memcpy(S, C, 2);
S[0] ^= Key[8]; S[1] ^= Key[9];
Substitution(S, inv);
S[0] ^= Key[6]; S[1] ^= Key[7];
for (i=0; i<round-1; i++) {
Permutation(S);
Substitution(S, inv);
S[0] ^= Key[(round/2-i)*2+0]; S[1] ^= Key[(round/2-i)*2+1];
}
memcpy(P, S, 2);
}
int main(int argc, char* argv[])
{
uint8_t C[2], P[2] = {0x11, 0x22}, D[2];
print("Key ", "\n", (uint8_t*)Key, 10);
print("P ", "\n", P, 2);
cipher(P, C);
print("C ", "\n", C, 2);
inv_cipher(C, D);
print("P ", "\n", D, 2);
return 0;
}
$ gcc --version && make clean && make && ./test.exe
gcc.exe (Rev2, Built by MSYS2 project) 6.2.0
Copyright (C) 2016 Free Software Foundation, Inc.
This is free software; see the source for copying conditions. There is NO
warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
rm -rf test *.o
cc -I. -Wall -Werror -O2 -c -o test.o test.c
cc -I. -Wall -Werror -O2 -o test test.o
Key 00 01 02 03 04 05 06 07 08 09
P 11 22
C 9E 46
P 11 22
[C2] Linear Approximation Table
# include <stdio.h>
# include <stdint.h>
static uint8_t Sbox[] = { 0xE, 0x4, 0xD, 0x1, 0x2, 0xF, 0xB, 0x8, 0x3, 0xA, 0x6, 0xC, 0x5, 0x9, 0x0, 0x7, };
static int8_t linear_approximation(uint8_t a, uint8_t b)
{
uint8_t X, Y; int8_t cnt= -8;
for (X=0; X<0x10; X++) {
uint8_t i, _X, _Y, xsum=0, ysum=0;
Y = Sbox[X];
_X = X & a;
_Y = Y & b;
for (i=0; i<4; i++) {
xsum ^= ((_X>>i) & 1);
ysum ^= ((_Y>>i) & 1);
}
if (xsum == ysum)
cnt++;
}
return cnt;
}
int main(int argc, char* argv[])
{
uint8_t a, b; // a1a2a3a4, b1b2b3b4
printf(" ");
for (b=0; b<0x10; b++) {
printf("%2X ", b);
}
printf("\n");
for (a=0; a<0x10; a++) {
printf("%01X ", a);
for (b=0; b<0x10; b++) {
printf("%+1d ", linear_approximation(a, b));
}
printf("\n");
}
return 0;
}
$ gcc --version && make clean && make && ./test.exe
gcc.exe (Rev2, Built by MSYS2 project) 6.2.0
Copyright (C) 2016 Free Software Foundation, Inc.
This is free software; see the source for copying conditions. There is NO
warranty; not even for MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.
rm -rf test *.o
cc -I. -Wall -Werror -O2 -c -o test.o test.c
cc -I. -Wall -Werror -O2 -o test test.o
0 1 2 3 4 5 6 7 8 9 A B C D E F
0 +8 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0 +0
1 +0 +0 -2 -2 +0 +0 -2 +6 +2 +2 +0 +0 +2 +2 +0 +0
2 +0 +0 -2 -2 +0 +0 -2 -2 +0 +0 +2 +2 +0 +0 -6 +2
3 +0 +0 +0 +0 +0 +0 +0 +0 +2 -6 -2 -2 +2 +2 -2 -2
4 +0 +2 +0 -2 -2 -4 -2 +0 +0 -2 +0 +2 +2 -4 +2 +0
5 +0 -2 -2 +0 -2 +0 +4 +2 -2 +0 -4 +2 +0 -2 -2 +0
6 +0 +2 -2 +4 +2 +0 +0 +2 +0 -2 +2 +4 -2 +0 +0 -2
7 +0 -2 +0 +2 +2 -4 +2 +0 -2 +0 +2 +0 +4 +2 +0 +2
8 +0 +0 +0 +0 +0 +0 +0 +0 -2 +2 +2 -2 +2 -2 -2 -6
9 +0 +0 -2 -2 +0 +0 -2 -2 -4 +0 -2 +2 +0 +4 +2 -2
A +0 +4 -2 +2 -4 +0 +2 -2 +2 +2 +0 +0 +2 +2 +0 +0
B +0 +4 +0 -4 +4 +0 +4 +0 +0 +0 +0 +0 +0 +0 +0 +0
C +0 -2 +4 -2 -2 +0 +2 +0 +2 +0 +2 +4 +0 +2 +0 -2
D +0 +2 +2 +0 -2 +4 +0 +2 -4 -2 +2 +0 +2 +0 +0 +2
E +0 +2 +2 +0 -2 -4 +0 +2 -2 +0 +0 -2 -4 +2 -2 +0
F +0 -2 -4 -2 -2 +0 +2 +0 +0 -2 +4 -2 -2 +0 +2 +0
[C3] Linear Cryptanalysis
# include <stdio.h>
# include <stdint.h>
# include <stdbool.h>
# include <string.h>
# include <stdlib.h>
# define COUNT (10000)
# define COUNTER_MAX (256)
//0x0, 0x1, 0x2, 0x3, 0x4, 0x5, 0x6, 0x7, 0x8, 0x9, 0xA, 0xB, 0xC, 0xD, 0xE, 0xF,
static const uint8_t Sbox[] = { 0xE, 0x4, 0xD, 0x1, 0x2, 0xF, 0xB, 0x8, 0x3, 0xA, 0x6, 0xC, 0x5, 0x9, 0x0, 0x7, };
static const uint8_t InvSbox[] = { 0xE, 0x3, 0x4, 0x8, 0x1, 0xC, 0xA, 0xF, 0x7, 0xD, 0x9, 0x6, 0xB, 0x2, 0x0, 0x5, };
static const uint8_t Key[] = { 0x11, 0x22, 0x33, 0x44, 0x55, 0x66, 0x77, 0x88, 0x99, 0xAA, }; // 5 x 16bit = 5 x 2byte = 10byte
static const int round = 4;
static uint16_t counter[COUNTER_MAX];
static void Substitution(uint8_t* S, bool is_inv)
{
uint8_t* box, _S[2];
if (is_inv) {
box = (uint8_t*)InvSbox;
} else {
box = (uint8_t*)Sbox;
}
_S[0] = box[S[0]&0x0F];
_S[0] |= (box[S[0]>>4]<<4);
_S[1] = box[S[1]&0x0F];
_S[1] |= (box[S[1]>>4]<<4);
memcpy(S, _S, 2);
}
static void Permutation(uint8_t* S)
{
uint8_t tmp[2];
/* bit0 */
tmp[0] = (S[0] & 0x80);
tmp[0] |= (S[0] & 0x08)<<3;
tmp[0] |= (S[1] & 0x80)>>2;
tmp[0] |= (S[1] & 0x08)<<1;
/* bit1 */
tmp[0] |= (S[0] & 0x40)>>3;
tmp[0] |= (S[0] & 0x04);
tmp[0] |= (S[1] & 0x40)>>5;
tmp[0] |= (S[1] & 0x04)>>2;
/* bit2 */
tmp[1] = (S[0] & 0x20)<<2;
tmp[1] |= (S[0] & 0x02)<<5;
tmp[1] |= (S[1] & 0x20);
tmp[1] |= (S[1] & 0x02)<<3;
/* bit3 */
tmp[1] |= (S[0] & 0x10)>>1;
tmp[1] |= (S[0] & 0x01)<<2;
tmp[1] |= (S[1] & 0x10)>>3;
tmp[1] |= (S[1] & 0x01);
memcpy(S, tmp, 2);
}
static void cipher(const uint8_t* P, uint8_t* C)
{
int i; bool inv = false;
uint8_t S[2];
memcpy(S, P, 2);
for (i=0; i<round-1; i++) {
S[0] ^= Key[i*2+0]; S[1] ^= Key[i*2+1];
Substitution(S, inv);
Permutation(S);
}
S[0] ^= Key[6]; S[1] ^= Key[7];
Substitution(S, inv);
S[0] ^= Key[8]; S[1] ^= Key[9];
memcpy(C, S, 2);
}
static void part_inv_cipher(uint8_t K, const uint8_t* C, uint8_t* U)
{
// K = K5-K8, K13-K16
U[0] = C[0] ^ (K>>4);
U[1] = C[1] ^ K;
Substitution(U, true /*inv*/);
}
static uint8_t sum(const uint8_t* P, const uint8_t* U)
{
uint8_t s = 0;
s ^= ((U[0]&0x4)>>2) ^ (U[0]&0x1) ^ ((U[1]&0x4)>>2) ^ (U[1]&0x1);
s ^= ((P[0]&0x8)>>3) ^ ((P[0]&0x2)>>1) ^ (P[0]&0x1);
return s;
}
static void count(const uint8_t* P, const uint8_t* C)
{
uint16_t K;
for (K=0; K<COUNTER_MAX; K++) {
uint8_t U[2];
part_inv_cipher(K, C, U);
counter[K] += sum(P, U);
}
}
int main(int argc, char* argv[])
{
uint16_t P, C, _P;
int i;
for (P=0; P<COUNT; P++) {
_P = P<<8 | P>>8;
cipher((uint8_t*)&_P, (uint8_t*)&C);
count((uint8_t*)&_P, (uint8_t*)&C);
}
for (i=0; i<COUNTER_MAX; i++) {
printf("%03d %02X\n", abs(counter[i] - COUNT/2), i);
}
return 0;
}
$ make clean && make && ./test.exe | sort -r | head
rm -rf test *.o
cc -I. -Wall -Werror -O2 -c -o test.o test.c
cc -I. -Wall -Werror -O2 -o test test.o
356 9A
262 5A
259 64
...
references
- [1] A Tutorial on Linear and Differential Cryptanalysis Howard M. Heys