はじめに
誤り検出に広く使われているCyclic Redundancy Check(CRC)について説明します。
誤り検出
誤り検出の概要を説明します。
ビット列の送受信を考えます。ビット列をメッセージといいます。
送信するメッセージをMsとします。受信するメッセージをMrとします。
送信側 Ms -> 伝送 -> Mr 受信側
メッセージだけでは誤りがあるかどうかの判定はできません。
誤り判定に使用するデータをメッセージに付加して送信します。付加するデータをチェックデータといいます。
送信側 Ms Cs -> 伝送 -> Mr Cr 受信側
送信側はMsに対して演算Opを行います。結果をCsとします。Ms Csを送信します。
受信側はMr Crを受信します。Mr Crに対して演算Opを行います。
結果が0であれば誤りなしと判定します。
CRCの演算
CRCの大まかな流れを説明します。
準備:
- 生成多項式P(G)を決めます。
- P(G)に対応するビット列Gを用意します。ビット長を$n$とします。
- P(G)/Gは送信・受信で共通使用します。
送信:
- Ms の下位ビット$n-1$を0で埋めます。
- Ms 0...0 を多項式と見立てます。
- Ms 0...0 をP(G)で除算します。
- 余り = CRC = Csは 下位ビット$n-1$に現れます。
- Ms Csを送信します。
受信:
- Mr Crを受信します。
- Mr Cr を多項式と見立てます。
- Mr Cr をP(G)で除算します。
- 下位ビット$n-1$がすべて0になれば誤りなしと判断します。
詳細を説明します。
{0,1}を2元体$F_2$の元と考えます。
ビット列を2元体を係数とする多項式とみなします。メッセージ多項式$P(Ms)$といいます。
メッセージのビット長を$n_m$とします。ビット列と多項式の対応は次の通りです。
Ms = Ms_{n_m-1}Ms_{n_m-2}...Ms_2Ms_1Ms_0 \\
P(Ms) = \sum_{i=0}^{n_m-1}{Ms_ix^i} = Ms_{n_m-1}x^{n_m-1} + Ms_{n_m-2}x^{n_m-2} + ... + Ms_2x^2 + Ms_1x + Ms_0 \\
Ms_i \in F_2 , i \in {n_m-1, n_m-2, ... ,2, 1, 0} \\
送信、受信共通で使用する多項式を決めます。生成多項式$P(G)$といいます。
生成多項式の次数+1を$n_g$とします。ビット列と多項式の対応は次の通りです。
G = G_{n_g-1}G_{n_g-2}...G_2G_1G_0 \\
P(G) = \sum_{i=0}^{n_g-1}{G_ix^i} = G_{n_g-1}x^{n_g-1} + G_{n_g-2}x^{n_g-2} + ... + G_2x^2 + G_1x + G_0 \\
G_i \in F_2 , i \in {n_g-1, n_g-2, ... ,2, 1, 0} \\
メッセージ多項式に$x^{n_g-1}$を掛けて生成多項式で除算して余りを求めます。余りを$P(Cs)$、商を$Q$とします。
P(Ms)x^{n_g-1} = Q P(G) + P(Cs) \\
P(Ms)x^{n_g-1} - P(Cs) = Q P(G) \\
\to P(Ms)x^{n_g-1} - P(Cs) = 0 \mod P(G) \\
送信データは$P(Ms)x^{n_g-1} - P(Cs)$に対応するビット列になります。ビット列と多項式の対応は次の通りです。
2元体での差は和と同じため$P(Ms)x^{n_g-1} - P(Cs) \to P(Ms)x^{n_g-1} + P(Cs)$とします。
Ms Cs = Ms_{n_m-1}Ms_{n_m-2}...Ms_2Ms_1Ms_0 Cs_{n_g-2}Cs_{n_g-3}...Cs_2C_1Cs_0 \\
P(Ms)x^{n_g-1} + P(Cs) = \sum_{i=0}^{n_m-1}{Mrix^{i+n_g-1}} + \sum_{j=0}^{n_g-2}{Csjx^j} \\
2元体を係数とする多項式を考える理由は以下の通りです。
- 多項式全体は多項式環になります。環となることから、余り、素数と類似の考え方が保証されます。
- 2元体であることから、余りを求める計算はXORの繰り返しです。単純なのでコンピュータ処理が容易です。
具体例
2元体を係数とする多項式の除法
具体的なメッセージ、生成多項式を考えて、多項式の除算を行い、CRCを求めてみます。
生成多項式
$n_g = 4$
G = 1011
$P(G) = x^3+x+1$
メッセージ
$n_m = 14$
Ms = 11010011101100
$P(Ms) = x^{13}+x^{12}+x^{10}+x^7+x^6+x^5+x^3+x^2$
Ms 000 <- 下位$n_g-1=3$に0を埋めます。
として余り(=CRC)を計算します。
XORを繰り返してCRCを計算します。結果は100になります。
--------------------
1011 | 11010011101100 000
1011
---------------------
1100
1011
---------------------
1110
1011
---------------------
1011
1011
---------------------
1101
1011
---------------------
1101
1011
---------------------
1100
1011
---------------------
1110
1011
---------------------
101 0
101 1
---------------------
100 <= CRC = Cs
送信側では Ms Cs = 11010011101100 100 を送信します。
受信側では Mr Cr に対して多項式の除算を行います。結果が0になれば誤りなしと判定します。
実装例
CRC16-IBM(0xA001) / CRC32(0xEDB88320)の実装例を次に示します。
右ビットシフトで演算しています。
9byteのASCII文字列"123456789"に対してCRCを計算します。
# include <stdio.h>
# include <string.h>
# include <stdint.h>
uint16_t crc16_table[256];
uint32_t crc32_table[256];
void make_crc16_table(void) {
for (uint16_t i = 0; i < 256; i++) {
uint16_t c = i;
for (int j = 0; j < 8; j++) {
c = (c & 1) ? (0xA001 ^ (c >> 1)) : (c >> 1);
}
crc16_table[i] = c;
}
}
uint16_t crc16(uint8_t *buf, size_t len) {
uint16_t c = 0;
for (size_t i = 0; i < len; i++) {
c = crc16_table[(c ^ buf[i]) & 0xFF] ^ (c >> 8);
}
return c;
}
void make_crc32_table(void) {
for (uint32_t i = 0; i < 256; i++) {
uint32_t c = i;
for (int j = 0; j < 8; j++) {
c = (c & 1) ? (0xEDB88320 ^ (c >> 1)) : (c >> 1);
}
crc32_table[i] = c;
}
}
uint32_t crc32(uint8_t *buf, size_t len) {
uint32_t c = 0xFFFFFFFF;
for (size_t i = 0; i < len; i++) {
c = crc32_table[(c ^ buf[i]) & 0xFF] ^ (c >> 8);
}
return c ^ 0xFFFFFFFF;
}
int main()
{
char* buf = "123456789";
int sz = strlen(buf);
uint16_t _crc16;
uint32_t _crc32;
printf("ascii=%s\n", buf);
make_crc16_table();
_crc16 = crc16((uint8_t*)buf, sz);
printf("crc16=%04x\n", _crc16);
make_crc32_table();
_crc32 = crc32((uint8_t*)buf, sz);
printf("crc32=%08x\n", _crc32);
return 0;
}
実行結果は次の通りです。
ascii=123456789
crc16=bb3d
crc32=cbf43926
バリエーション
CRCには多くの実装が存在しており様々なバリエーションがあります。
パラメータは送信・受信で一致させる必要があります。
主なパラメータは次の通りです。
- 生成多項式
- ビットシフトの方向
- 初期値
- 除算後のXOR
生成多項式
よく利用される生成多項式は次の通りです。
Normal / Bit reversed
CRC16-IBM : 0x1021 / 0x8408
CRC32 : 0x04C11DB7 / 0xEDB88320
※先頭1ビットは省略されています。CRC16-IBMを例に説明します。
生成多項式をビットに対応させると0x11021となりますが先頭の0x1は省略します。
CRCを計算するときに先頭1ビットは常に無視することが可能だからです。
Normalは左ビットシフトで使用します。
Bit reversedは右ビットシフトで使用します。
ビットシフトの方向
除算するとき、割られる数を左右どちらにビットシフトするかを決める必要があります。
左ビットシフトの例です。割られる数の最も左側のビットが0になるように演算を進めます。
----------
1011 | 11010011
1011
----------
1100
1011
(snip)
右ビットシフトの例です。割られる数の最も右側のビットが0になるように演算を進めます。
----------
1101 | 11001011
1101
----------
0011
1101
(snip)
初期値
除算を行う前の初期値を指定します。
CRC32では初期値0xFFFFFFFFを使います。
以下実装例の抜粋です。
uint32_t crc32(uint8_t *buf, size_t len) {
uint32_t c = 0xFFFFFFFF;
(snip)
}
除算後のXOR
除算後の余りに対して一定パターンのXORを指定します。
CRC32では初期値0xFFFFFFFFを使います。
以下実装例の抜粋です。
uint32_t crc32(uint8_t *buf, size_t len) {
(snip)
return c ^ 0xFFFFFFFF;
}
計算の効率化
先頭ビットの処理
先頭ビットは常に1のため除算すると必ず0になります。
したがって先頭ビットの処理は省略できます。
具体例として除算の途中結果を示します。
--------------------
1011 | 11010011101100 000
1011
---------------------
1100
1011
---------------------
1110
1011
(snip)
省略後の処理は以下です。
--------------------
(*1) 011 |11010011101100 000 (*2)
011
---------------------
1100 (*2)
011
---------------------
1110 (*2)
011
(snip)
生成多項式の先頭ビットを省略しています。(*1)
割る数(*2)の先頭ビットが1の時に先頭ビットは除外して生成多項式を1ビットずらして除算します。
標準的な生成多項式のビット表記はあらかじめ先頭ビットが除外されています。
以下実装例の抜粋です。
c = (c & 1) ? (0xA001 ^ (c >> 1)) : (c >> 1);
テーブルの利用
生成多項式と0~255の除算結果をテーブルにすることで除算を省略できます。
以下実装例の抜粋です。
void make_crc16_table(void) {
for (uint16_t i = 0; i < 256; i++) {
uint16_t c = i;
for (int j = 0; j < 8; j++) {
c = (c & 1) ? (0xA001 ^ (c >> 1)) : (c >> 1);
}
crc16_table[i] = c;
}
}
除算結果を256個のテーブルに保持します。
crc16_table[i] = c;
テーブルを使って複数バイトの除算を行います。
以下実装例の抜粋です。
uint16_t crc16(uint8_t *buf, size_t len) {
uint16_t c = 0;
for (size_t i = 0; i < len; i++) {
c = crc16_table[(c ^ buf[i]) & 0xFF] ^ (c >> 8);
}
return c;
}
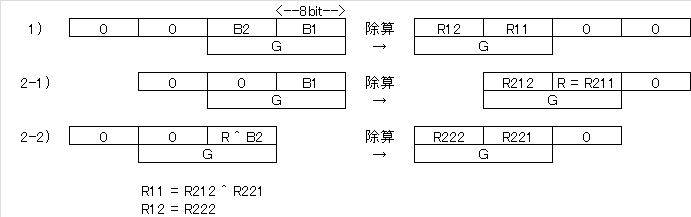
メッセージが2バイトB1/B2で構成される例です。Gは生成多項式です。
1)はテーブルを使わないで除算するケースです。
2-1)/2-2)はテーブルを使って除算するケースです。
indexにB1を指定することで R=R211とR212が取り出せます。
indexにR^B2を指定することでR221とR222が取り出せます。
1)のR11 = R212 ^ R221, R12 = R222に対応します。
このようにしてテーブルを使った除算を行います。
実装例では以下で上記処理を行っています。
c = crc16_table[(c ^ buf[i]) & 0xFF] ^ (c >> 8);
Appendix
2元体と多項式環の説明をします。
2元体
2元体とは構成要素が2つの体(Field)です。2つの元を{0, 1}と表記します。
体とは四則演算できる集合です。
和
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 -> 1 = -1
積
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1
和はXOR(排他的論理和)であることと、差は和と同じであることに注目してください。
多項式環
多項式環について説明します。
2元体を係数とする多項式全体を$P$と表します。任意の$f,g \in P$を考えます。$f_i,g_i \in GF(2)$
2元体の係数を用いて$f,g$を次のように表します。
f = \sum_{i=0}^{m}{f_ix^i} \\
g = \sum_{i=0}^{n}{g_ix^i} \\
多項式の和と積を次のように定義します。
2元体の和と積に還元されていることに注目してください。
和
f + g = \sum_{i=0}^{max\{m,n\}}({f_i}+{g_i})x^i \\
積
f * g = (\sum_{i=0}^{m}{f_ix^i})(\sum_{j=0}^{n}{g_jx^j}) \\
= \sum_{i=0}^{m+n}(\sum_{j=0}^{i}{f_jg_{i-j}})x^i
上に定義した和と積に関して環(ring)になっていることが知られています。多項式環といいます。
多項式環の性質から次の剰余定理が成り立ちます。
a,b \in P \\
a = q b + r \\
となる q, r \in Pが一意に存在する。 (rの次数) < (bの次数)となる。
これにより$a$を$b$で割ったとき、商$q$、余り$r$が存在することが保証されます。
$r=0$の時、$b$は$a$を割り切るといいます。$a$は$b$の倍数、$b$は$a$の因数といいます。
$p \in P$が自分自身と1以外で割り切れない場合、$p$を既約多項式といいます。
素数とおなじ性質があり、誤り検出の効率が良いことから既約多項式を生成多項式とすることが多いです。
CRC32左ビットシフト版
# include <stdio.h>
# include <string.h>
# include <stdint.h>
uint32_t crc32_table[256];
void make_crc32_table(void) {
for (uint32_t i = 0; i < 256; i++) {
uint32_t c = i << 24;
for (int j = 0; j < 8; j++) {
c = (c << 1) ^ ((c & 0x80000000) ? 0x04c11db7 : 0);
}
crc32_table[i] = c;
}
}
uint32_t crc32(uint8_t *buf, size_t len) {
uint32_t c = 0xFFFFFFFF;
for (size_t i = 0; i < len; i++) {
c = (c << 8) ^ crc32_table[((c >> 24) ^ buf[i]) & 0xFF];
}
return c;
}
int main()
{
char* buf = "123456789";
int sz = strlen(buf);
uint32_t _crc32;
printf("ascii=%s\n", buf);
make_crc32_table();
_crc32 = crc32((uint8_t*)buf, sz);
printf("crc32=%08x\n", _crc32);
return 0;
}
references
Cyclic redundancy check
Mathematics of cyclic redundancy checks
Polynomial ring