Pythonで常微分方程式を解く

はじめに

Pythonを使って常微分方程式を解く方法を説明します。

OS / Python module version

使用したOSはWindows 10 です。
Python module versionは次の通りです。

console

> python --version
Python 3.4.3
> pip freeze
matplotlib==1.4.3
numpy==1.13.1+mkl
pandas==0.16.2
pyparsing==2.0.3
python-dateutil==2.4.2
pytz==2015.4
scipy==0.19.1
six==1.9.0

sample code

次の微分方程式を解きます。

y'' = -y \\

変数zを導入します。
変数を増やすことで1つの2階微分方程式を2つの1階微分方程式の連立方程式と考えます。

y' = z \\
z' = -y \\

初期条件を $t=0, y_0 = 1, z_0 = 0$とします。
解は$cos(t)$となります。正しい解が容易に求められますので誤差の評価ができます。

微分方程式を解くPythonプログラムを次に示します。
scipy.integrate.odeを使って解きます。

test.py

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import ode

def f(t, v): # t, y:v[0], y'=z:v[1]
    return [v[1], -v[0]] # y':return[0] y''=z':return[1]
v0 = [1.0, 0.0] # y0, y'0=z0

solver = ode(f)
solver.set_integrator(name="dop853")
solver.set_initial_value(v0)
tw = 10.0*2.0*np.pi
dt = tw / 1000;
t = 0.0
ts = []
ys = []
while solver.t < tw:
    solver.integrate(solver.t+dt)
    ts += [solver.t]
    ys += [solver.y[0]]
plt.figure(0)
plt.plot(ts, ys)
plt.figure(1)
plt.plot(ts, np.cos(ts)-ys)
plt.show()
print(np.max(np.cos(ts)-ys))

実行します。

console

> python .\test.py

実行するとグラフが表示されます。

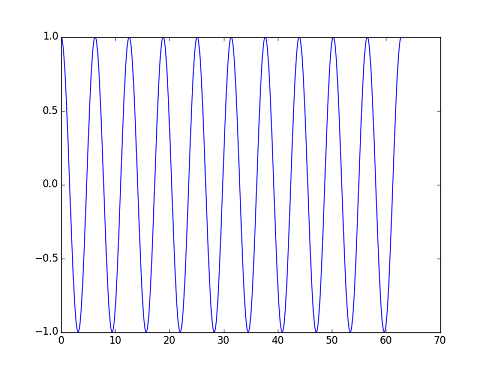
次のグラフは微分方程式の解です。cos(t)のグラフが10周期分表示されています。

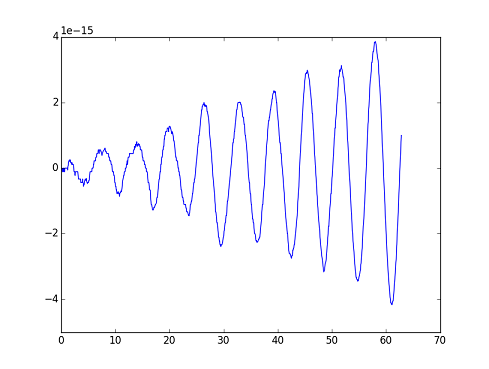
次のグラフは誤差をプロットしています。tが増えるにつれて誤差も増えています。
誤差は$10^{-15}$のスケールになります。