はじめに
Fast cosine transformを説明します。B.G. Lee のPaperを参照します。
B. G. Lee A new algorithm to compute the discrete cosine transform
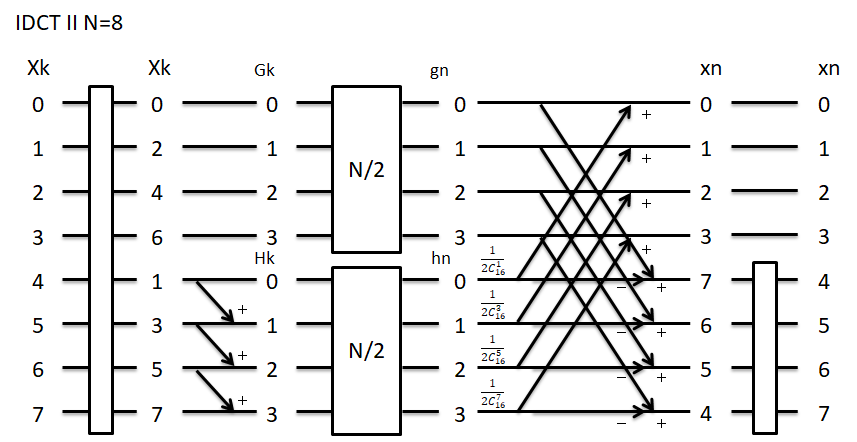
inverse DCT II
定義式は次の通りです。簡略化のため$C_{2N}^{(2n+1)k} = \cos \frac{\pi}{2N} (2n+1)k$と表記します。
\begin{eqnarray}
x_n &=& \sum_{k=0}^{N-1} X_k C_{2N}^{(2n+1)k} \\
\end{eqnarray}
kについて偶数と奇数に分けます。
\begin{eqnarray}
x_n &=&
\left\{
\begin{array}{ll}
g_n &=& \sum_{k=0}^{N/2-1} X_{2k} C_{2N}^{(2n+1)2k} \\
h'_n &=& \sum_{k=0}^{N/2-1} X_{2k+1} C_{2N}^{(2n+1)(2k+1)} \\
\end{array}
\right. \\
\end{eqnarray}
nについて前半 N/2 と 後半 N/2 に分けます。
次が成り立ちます。n=0 ... N/2-1 です。
\begin{eqnarray}
x_n &=& g_n + h'_n \\
x_{N-1-n} &=& g_n - h'_n \\
\end{eqnarray}
上記を示します。前半は自明です。後半 N/2 が成り立つことを説明します。
\begin{eqnarray}
x_{N-1-n} &=& \sum_{k=0}^{N/2-1} X_k C_{2N}^{(2(N-1-n)+1)k} \\
C_{2N}^{(2(N-1-n)+1)k} &=& C_{2N}^{2Nk-(2n+1)k} = \cos \left( k \pi - \frac{\pi (2n+1)k}{2N} \right) \\
\end{eqnarray}
次の関係式から後半が成り立つことが分かります。
\begin{eqnarray}
\cos \left(n \pi - \theta \right) =
\left\{
\begin{array}{ll}
+ \cos \theta & (n = even) \\
- \cos \theta & (n = odd) \\
\end{array}
\right. \\
\end{eqnarray}
次に再帰的に処理を行うために $g_n,h'_n$ を $x_n$と同じ式の形にします。
$x_n$は次の形でした。
\begin{eqnarray}
x_n &=& \sum_{k=0}^{N-1} X_{k} C_{2N}^{(2n+1)k} \\
\end{eqnarray}
$g_n$について考えます。
\begin{eqnarray}
g_n &=& \sum_{k=0}^{N/2-1} X_{2k} C_{2N}^{(2n+1)2k} \\
&=& \sum_{k=0}^{N/2-1} X_{2k} C_{2(N/2)}^{(2n+1)k} \\
G_k &=& X_{2k} \\
g_n &=& \sum_{k=0}^{N/2-1} G_k C_{2(N/2)}^{(2n+1)k} \\
\end{eqnarray}
$h'_n$について考えます。
\begin{eqnarray}
h'_n &=& \sum_{k=0}^{N/2-1} X_{2k+1} C_{2N}^{(2n+1)(2k+1)} \\
\end{eqnarray}
次の公式を使うことで、
\begin{eqnarray}
2\cos \alpha \cos \beta = \cos (\alpha + \beta) + \cos (\alpha - \beta)
\end{eqnarray}
次のように式変形できます。
\begin{eqnarray}
2 C_{2N}^{(2n+1)} C_{2N}^{(2n+1)(2k+1)} &=& C_{2N}^{(2n+1)2k} + C_{2N}^{(2n+1)2(k+1)} \\
\end{eqnarray}
上記を$h'_n$に適用します。
\begin{eqnarray}
2 C_{2N}^{(2n+1)} h'_n &=& \sum_{k=0}^{N/2-1} X_{2k+1} \left( C_{2N}^{(2n+1)2k} + C_{2N}^{(2n+1)2(k+1)} \right) \\
\end{eqnarray}
上記右辺2項を次のように変形します。
右肩の$2(k+1)$ を $2k$ にするために、2つ前の$X$を使います。
\begin{eqnarray}
\sum_{k=0}^{N/2-1} X_{2k+1} C_{2N}^{(2n+1)2(k+1)} &=& \sum_{k=0}^{N/2-1} X_{2k-1} C_{2N}^{(2n+1)2k} \\
\end{eqnarray}
\begin{eqnarray}
X_{-1} &=& 0 \\
C_{2N}^{(2n+1)2(N/2)} &=& C_{2}^{(2n+1)} = 0 \\
\end{eqnarray}
上記を$h'_n$に適用します。
\begin{eqnarray}
2 C_{2N}^{(2n+1)} h'_n &=& \sum_{k=0}^{N/2-1} \left( X_{2k+1} + X_{2k-1} \right) C_{2N}^{(2n+1)2k} \\
h'_n &=& \frac{1}{2 C_{2N}^{(2n+1)}} \sum_{k=0}^{N/2-1} H_k C_{2(N/2)}^{(2n+1)k} = \frac{1}{2 C_{2N}^{(2n+1)}} h_n \\
h_n &=& \sum_{k=0}^{N/2-1} H_k C_{2(N/2)}^{(2n+1)k} \\
H_n &=& X_{2k+1} + X_{2k-1} \\
\end{eqnarray}
式をまとめます。$x_n$は次の通りです。
\begin{eqnarray}
x_n &=& \sum_{k=0}^{N-1} X_k C_{2N}^{(2n+1)k} \\
n &=& 0,..., N-1 \\
\end{eqnarray}
$g_n,h_n$は次の通りです。
\begin{eqnarray}
g_n &=& \sum_{k=0}^{N/2-1} G_k C_{2(N/2)}^{(2n+1)k} \\
h_n &=& \sum_{k=0}^{N/2-1} H_k C_{2(N/2)}^{(2n+1)k} \\
n &=& 0,..., N/2-1 \\
\end{eqnarray}
$G_k,H_k$を$X_k$で表します。
\begin{eqnarray}
G_k &=& X_{2k} \\
H_k &=& X_{2k+1} + X_{2k-1} \\
\end{eqnarray}
$x_k$を$g_k,h_k$で表します。
\begin{eqnarray}
x_n &=& g_n + \frac{1}{2 C_{2N}^{(2n+1)}} h_n \\
x_{N-1-n} &=& g_n - \frac{1}{2 C_{2N}^{(2n+1)}} h_n \\
\end{eqnarray}
次にフロー図を示します。N=8の場合です。
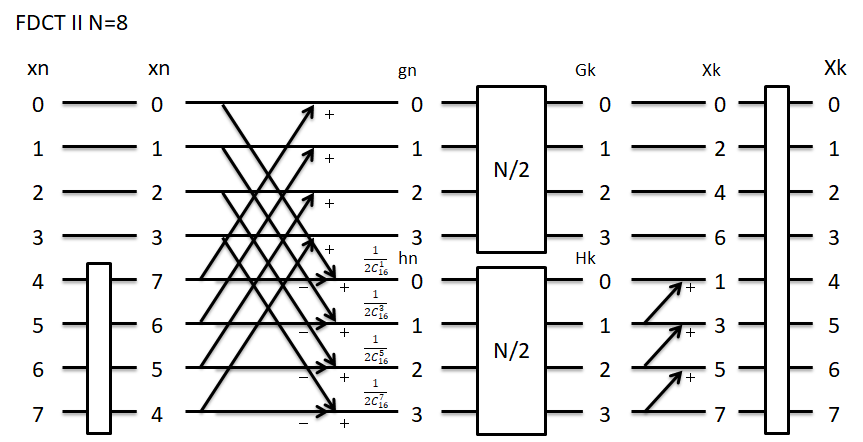
forward DCT II
定義式は次の通りです。
\begin{eqnarray}
X_k &=& \sum_{n=0}^{N-1} x_n C_{2N}^{(2n+1)k} \\
\end{eqnarray}
nについて前半 N/2 と 後半 N/2 に分けます。
次が成り立ちます。n=0 ... N/2-1 です。
\begin{eqnarray}
X_k &=& \sum_{n=0}^{N/2-1} x_n C_{2N}^{(2n+1)k} + \sum_{n=0}^{N/2-1} x_{N-1-n} C_{2N}^{(2(N-1-n)+1)k} \\
\end{eqnarray}
kについて偶数と奇数に分けます。
\begin{eqnarray}
X_{2k}
&=& \sum_{n=0}^{N/2-1} x_n C_{2N}^{(2n+1)2k} + \sum_{n=0}^{N/2-1} x_{N-1-n} C_{2N}^{(2(N-1-n)+1)2k} \\
&=& \sum_{n=0}^{N/2-1} x_n C_{2N/2}^{(2n+1)k} + \sum_{n=0}^{N/2-1} x_{N-1-n} C_{2N/2}^{(2n+1)k} \\
&=& \sum_{n=0}^{N/2-1} (x_n - x_{N-1-n}) C_{2N/2}^{(2n+1)k} = \sum_{n=0}^{N/2-1} g_n C_{2N/2}^{(2n+1)k} = G_k \\
X_{2k+1}
&=& \sum_{n=0}^{N/2-1} x_n C_{2N}^{(2n+1)(2k+1)} + \sum_{n=0}^{N/2-1} x_{N-1-n} C_{2N}^{(2(N-1-n)+1)(2k+1)} \\
&=& \sum_{n=0}^{N/2-1} x_n C_{2N}^{(2n+1)(2k+1)} - \sum_{n=0}^{N/2-1} x_{N-1-n} C_{2N}^{(2n+1)(2k+1)} \\
&=& \sum_{n=0}^{N/2-1} (x_n - x_{N-1-n}) C_{2N}^{(2n+1)(2k+1)} \\
&=& \sum_{n=0}^{N/2-1} \frac{(x_n - x_{N-1-n})}{2 C_{2N}^{(2n+1)}} \left (C_{2N/2}^{(2n+1)(k+1)} + C_{2N/2}^{(2n+1)k} \right) \\
&=& \sum_{n=0}^{N/2-1} h_n \left (C_{2N/2}^{(2n+1)(k+1)} + C_{2N/2}^{(2n+1)k} \right) = H_{k+1} + H_k \\
\end{eqnarray}
式をまとめます。$X_n$は次の通りです。
\begin{eqnarray}
X_k &=& \sum_{n=0}^{N-1} x_n C_{2N}^{(2n+1)k} \\
k &=& 0, ..., N-1 \\
\end{eqnarray}
$G_n, H_n$は次の通りです。
\begin{eqnarray}
G_k &=& \sum_{n=0}^{N/2-1} g_n C_{2N/2}^{(2n+1)k} \\
H_k &=& \sum_{n=0}^{N/2-1} h_n C_{2N/2}^{(2n+1)k} \\
k &=& 0, ..., N/2-1 \\
\end{eqnarray}
$g_n, h_n$を$x_n$で表します。
\begin{eqnarray}
g_n &=& x_n + x_{N-1-n} \\
h_n &=& \frac{x_n - x_{N-1-n}}{2 C^{2n+1}_{2N}} \\
\end{eqnarray}
$X_k$を$G_k,H_k$で表します。
\begin{eqnarray}
X_{2k} &=& G_k \\
X_{2k+1} &=& H_k + H_{k+1} \\
\end{eqnarray}
次にフロー図を示します。N=8の場合です。
DCT IV
DCT IVはDCT IIに変換できます。次のようにして変換します。
\begin{eqnarray}
x_n
&=& \sum_{k=0}^{N-1}{X_k C_{4N}^{(2n+1)(2k+1)}} \\
&=& \frac{1}{2 C_{4N}^{2n+1}} \sum_{k=0}^{N-1}{X_k \left( C_{2N}^{(2n+1)k} + C_{2N}^{(2n+1)(k+1)} \right) } \\
&=& \frac{1}{2 C_{4N}^{2n+1}} \sum_{k=0}^{N-1}{(X_{k-1} + X_k) C_{2N}^{(2n+1)k}} \\
&=& \frac{1}{2 C_{4N}^{2n+1}} y_n \\
y_n &=& \sum_{k=0}^{N-1}{Y_k C_{2N}^{(2n+1)k}} \\
Y_k &=& X_{k-1} + X_k \\
\end{eqnarray}
code example
CFLAGS=-I. -Wall -Werror -O2 -march=native
INCS=
OBJS=test.o
LIBS=
TARGET=test
%.o: %.c $(INCS)
$(CC) $(CFLAGS) -c -o $@ $<
$(TARGET): $(OBJS)
$(CC) $(CFLAGS) -o $@ $^ $(LIBS)
clean:
rm -rf $(TARGET) *.o
# include <math.h>
# include <stdio.h>
# include <string.h>
const double C4[] = {
7.07106781186548E-01,
};
const double C8[] = {
5.41196100146197E-01, // 1/(2*cos(pi/8*1))
1.30656296487638E+00, // 1/(2*cos(pi/8*3))
};
const double C16[] = {
5.09795579104159E-01, // 1/(2*cos(pi/16*1))
6.01344886935045E-01, // 1/(2*cos(pi/16*3))
8.99976223136416E-01, // 1/(2*cos(pi/16*5))
2.56291544774151E+00, // 1/(2*cos(pi/16*7))
};
const double C32[] = {
5.02419286188156E-01, // 1/(2*cos(pi/32*1))
5.22498614939689E-01, // 1/(2*cos(pi/32*3))
5.66944034816358E-01, // 1/(2*cos(pi/32*5))
6.46821783359990E-01, // 1/(2*cos(pi/32*7))
7.88154623451250E-01, // 1/(2*cos(pi/32*9))
1.06067768599035E+00, // 1/(2*cos(pi/32*11))
1.72244709823833E+00, // 1/(2*cos(pi/32*13))
5.10114861868916E+00, // 1/(2*cos(pi/32*15))
};
static void idctII2(double* input, double* output)
{
double* x = output;
double* X = input;
double tmp = C4[0] * X[1];
x[0] = X[0] + tmp;
x[1] = X[0] - tmp;
}
static void idctII4(double* input, double* output)
{
double* x = output;
static double in[2], g[2], h[2], tmp[2];
in[0] = input[0];
in[1] = input[2];
idctII2(in, g);
in[0] = input[1];
in[1] = input[3] + input[1];
idctII2(in, h);
tmp[0] = C8[0] * h[0];
tmp[1] = C8[1] * h[1];
x[0] = g[0] + tmp[0];
x[1] = g[1] + tmp[1];
x[2] = g[1] - tmp[1];
x[3] = g[0] - tmp[0];
}
static void idctII8(double* input, double* output)
{
double* x = output;
static double in[4], g[4], h[4], tmp[4];
in[0] = input[0];
in[1] = input[2];
in[2] = input[4];
in[3] = input[6];
idctII4(in, g);
in[0] = input[1];
in[1] = input[3] + input[1];
in[2] = input[5] + input[3];
in[3] = input[7] + input[5];
idctII4(in, h);
tmp[0] = C16[0] * h[0];
tmp[1] = C16[1] * h[1];
tmp[2] = C16[2] * h[2];
tmp[3] = C16[3] * h[3];
x[0] = g[0] + tmp[0];
x[1] = g[1] + tmp[1];
x[2] = g[2] + tmp[2];
x[3] = g[3] + tmp[3];
x[4] = g[3] - tmp[3];
x[5] = g[2] - tmp[2];
x[6] = g[1] - tmp[1];
x[7] = g[0] - tmp[0];
}
static void fdctII2(double* input, double* output)
{
double* X = output;
double* x = input;
X[0] = x[0] + x[1];
X[1] = (x[0] - x[1]) * C4[0];
}
static void fdctII4(double* input, double* output)
{
double* X = output;
static double in[2], G[2], H[2];
in[0] = input[0] + input[3];
in[1] = input[1] + input[2];
fdctII2(in, G);
in[0] = C8[0] * (input[0] - input[3]);
in[1] = C8[1] * (input[1] - input[2]);
fdctII2(in, H);
X[0] = G[0];
X[1] = H[0] + H[1];
X[2] = G[1];
X[3] = H[1];
}
static void fdctII8(double* input, double* output)
{
double* X = output;
static double in[4], G[4], H[4];
in[0] = input[0] + input[7];
in[1] = input[1] + input[6];
in[2] = input[2] + input[5];
in[3] = input[3] + input[4];
fdctII4(in, G);
in[0] = C16[0] * (input[0] - input[7]);
in[1] = C16[1] * (input[1] - input[6]);
in[2] = C16[2] * (input[2] - input[5]);
in[3] = C16[3] * (input[3] - input[4]);
fdctII4(in, H);
X[0] = G[0];
X[1] = H[0] + H[1];
X[2] = G[1];
X[3] = H[1] + H[2];
X[4] = G[2];
X[5] = H[2] + H[3];
X[6] = G[3];
X[7] = H[3];
}
static void dctIV8(double* input, double* output)
{
int i;
static double in[8];
in[0] = input[0];
for (i=1; i<8; i++) {
in[i] = input[i-1] + input[i];
}
idctII8(in, output);
for (i=0; i<8; i++) {
output[i] *= C32[i];
}
}
static void print_data(const char* str, const double *data, int N)
{
int i;
printf("%s", str);
for (i=0; i<N; i++) {
printf("%+1.3e ", data[i]);
}
printf("\n");
}
int main(int argc, char* argv[])
{
double input[] = {0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0};
double output[8];
print_data("input\n", input, 8);
memset(output, 0, sizeof(output));
fdctII8(input, output);
print_data("fdctII8\n", output, 8);
memset(output, 0, sizeof(output));
idctII8(input, output);
print_data("idctII8\n", output, 8);
memset(output, 0, sizeof(output));
dctIV8(input, output);
print_data("dctIV8\n", output, 8);
return 0;
}
$ make;./test.exe
cc -I. -Wall -Werror -O2 -march=native -c -o test.o test.c
cc -I. -Wall -Werror -O2 -march=native -o test test.o
input
+0.000e+000 +1.000e+000 +2.000e+000 +3.000e+000 +4.000e+000 +5.000e+000 +6.000e+000 +7.000e+000
fdctII8
+2.800e+001 -1.288e+001 +0.000e+000 -1.347e+000 +0.000e+000 -4.018e-001 +0.000e+000 -1.014e-001
idctII8
+1.459e+001 -1.615e+001 +6.358e+000 -5.495e+000 +2.864e+000 -2.459e+000 +9.404e-001 -6.464e-001
dctIV8
+1.236e+001 -1.576e+001 +6.963e+000 -6.391e+000 +4.586e+000 -4.404e+000 +3.839e+000 -3.793e+000