はじめに
こちらの記事で、CODE FESTIVALという競技プログラミングのイベントの過去問題について紹介しました。
私も解いてみることに。
ただし私のプログラミングの腕前の都合上、D問題以降は解ける気がしないので、A~C問題をやります。
この記事では感想を書きます。
A問題の感想
簡単だったのであんまりコメントすることないです。
例えば2014予選AのA問題は、文字列 $S$ の後ろに文字列 "2014" をくっつけるだけでそれが答えになりました(私はJavaでやっているので + で連結)。
面白かったのは2015予選BのA問題ですね。
B問題の感想
2014予選A B - とても長い文字列
問題へのリンク / 私の提出ソースコード
$B$ を $A$ の長さで割ったあまりを使って答えを出せました。周期性が重要!
2014予選B B - 歩く人
問題へのリンク / 私の提出ソースコード
配列の中身をただ足し算していくだけ!
2015予選A B - とても長い数列
問題へのリンク / 私の提出ソースコード
公式解説によると、問題文のとおりに素直にシミュレーションするのが部分点解法で、DPするのが満点解法のようです。しかし私は、
配列Aの後ろから1, 2, 3, 4, 5, 6, …番目の数字は、
とても長い数列に1, 2, 4, 8, 16, 32, …個登場する
という規則(入出力例からなんとなく想像可能)を使って答えを計算で求めました。
2015予選B B - 採点
問題へのリンク / 私の提出ソースコード
100個の数字があるので50回より多く登場する数字を答えよ、といった問題です。多数決みたいな感じですね。
普通にカウントしてもよいのですが、私は100個の数字をソートしてずらっと並べて、同じ数字が51個連続しているところを探して解きました。
「同じ数字が51個並んでいるか?」については、51個確認する必要はなくて、左端と右端だけ見れば判定できます。ソート済みなので。
2016予選A B - 仲良しうさぎ
問題へのリンク / 私の提出ソースコード
両想いなペアを数える問題です。
うさぎAとうさぎBが両想いのとき、うさぎAでスコア+1、うさぎBでもスコア+1、と2重カウントしてしまうのが罠になっています。
「うさぎAとうさぎBは両想いか?」は判定するけど「うさぎBとうさぎAは両想いか?」のように番号が逆行しているときは判定しないというプログラムにすることで罠を回避しましたが、作者解法は普通に2重カウントしたあと最後にスコアを2で割ってました。頭良い。
2016予選B B - Qualification simulator
問題へのリンク / 私の提出ソースコード
これは素直に問題文どおりにシミュレーション!
2016予選C B - K個のケーキ
問題へのリンク / 私の提出ソースコード
同じケーキを連続で食べるのは嫌だ!という問題です。
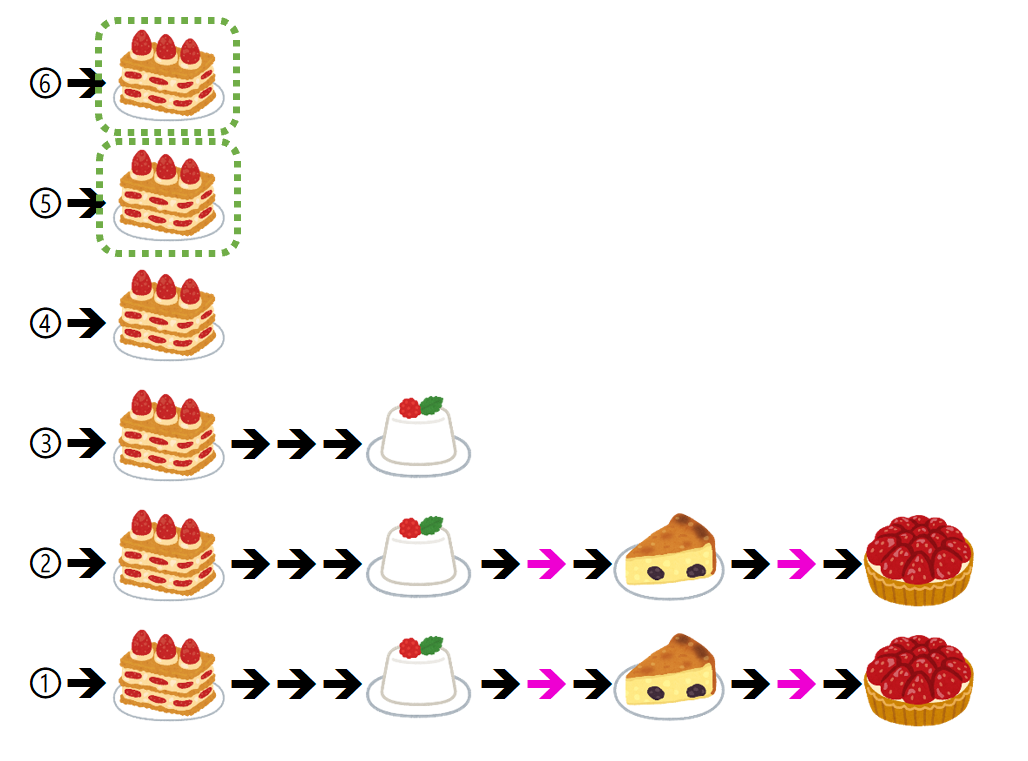
上図のように、①段目⇒②段目⇒③段目⇒…と食べようと考えました。スイーツバイキングで「全ケーキを1個ずつ取ってくる」を何周もするわけです。ただしこれだと最も多いケーキが最後に余る(上図の緑)ので、そういったケーキは他のケーキの隙間(上図のピンク)に割り込ませるという方針で実装したところ、その方針で正解できました。
ちなみに別案として、最も多いケーキ(上図だとミルフィーユ)の隙間に他のケーキを割り込ませるという解法も思いつきました。作者解法もそうやっていました。まぁたしかにそのほうが実装は楽ですよね。
2017予選A B - fLIP
問題へのリンク / 私の提出ソースコード
パズルゲームです。「ボタンを何個押したかが重要」「どのボタンを押したかは重要でない」「同じボタンを二度押すのは無意味」といった観察に気づくことができたので解けました。
2017予選B B - Problem Set
問題へのリンク / 私の提出ソースコード
なにかうまいやり方があるのだろうとは思いつつ、普通にアイテムを当てはめていく方針でやりました。
2017予選C B - Similar Arrays
問題へのリンク / 私の提出ソースコード
これは良い問題ですね。ひらめいたとき脳汁が出ました。
2018予選A B - みかん
問題へのリンク / 私の提出ソースコード
推理のヒントが $M$ 個与えられますが、あるヒントと別のヒントで情報がダブっていることがあります。みかん1つに対しての情報は1回でいいので、ダブりは計算の無駄です。無駄をどう省くか?…と一瞬身構えましたが、制約を見たらたったの $M≤100$ だったので無駄な情報をそのまま全部読み込んで正解できました。ありがとう制約。
2018予選B B - Tensai
問題へのリンク / 私の提出ソースコード
最適戦術がすぐ分かったので簡単でした。ていうか問題文の1行目がギャグっぽいんですが事実なんですかね…?
以上で各コンテストのB問題はすべて解けました!
C問題の感想
2014予選A C - 2月29日
問題へのリンク / 私の提出ソースコード
「$A$ 以上 $B$ 以下の範囲に $n$ で割り切れる整数はいくつあるか?」という小問題を考えて、それの答えを $f(n)$ とすると、元の問題の答えは $f(4)-f(100)+f(400)$ で得られることに気づきました。無事正解。
2014予選B C - 錬金術士
問題へのリンク / 私の提出ソースコード
自力で解けなかったので公式解説スライドを見ました。悔しい~。でも理解できてスッキリ。
例えば
・S1:AAAAABCCCCC
・S2:AABBBBCCCCC
・S3:AAAABBCCCCC
だったら、
・S1から取り出すAは、最小で2個、最大で4個
・S1から取り出すBは、最小で0個、最大で1個
・S1から取り出すCは、最小で0個、最大で4個
ですので、「2, 3, 4のいずれか」+「0, 1のいずれか」+「0, 1, 2, 3, 4のいずれか」= 5 にできるか?を判定すればいいわけですね。
「ある文字をS1とS2から何個ずつ取ればいいか」を求めようとしてしまったのは失敗でした。
2015予選A C - 8月31日
問題へのリンク / 私の提出ソースコード
戦略としては「写したときの効果が大きいものから写す」でOKです。ところが $n$ 個全部写したときの判定処理を書き忘れるという凡ミスをしてしまい、2回目の提出で正解。
2015予選B C - 旅館
問題へのリンク / 私の提出ソースコード
「2017予選B B - Problem Set」とほぼ同じ問題です。ソースコードをまるごとコピペして、条件式をちょろっと変えただけで正解。
2016予選A C - 次のアルファベット
問題へのリンク / 私の提出ソースコード
最適戦略は自分でひらめくことができましたが、ちょっとした凡ミス(元々 'a' ならそのままでいいのに $K$ を26回消費して 'a' にしてた)をやってしまい2回目の提出で正解。なにやってんだか。
2016予選B C - Gr-idian MST
問題へのリンク / 私の提出ソースコード
タイトルにもあるとおりMSTです。というわけでクラスカル法です。普通にやると辺の数が $WH+W+H$ もあって死んでしまいますが、辺の配置もコストの配置も規則的であることを利用し、グラフの隣接リストを使わず工夫して解く感じの問題でした。面白かったです。一発正解できたのも嬉しい。
2016予選C C - 二人のアルピニスト
問題へのリンク / 私の提出ソースコード
問題ページには二人が全て登り切った後の意見食い違いによる矛盾が書いてありますが、矛盾が発生しうる原因はこれだけではありません。例えば入力が
$6$
$2$ $3$ $3$ $3$ $5$ $5$
$6$ $6$ $5$ $4$ $4$ $4$
だと以下のような矛盾があります。
- 山2:高橋君によると高さ3確定だが、青木君によると高さ6確定
- 山3:高橋君によると高さ3以下だが、青木君によると高さ5確定
- 山5:高橋君によると高さ5確定だが、青木君によると高さ4以下
このように「確定」と「確定」が嚙み合わない矛盾もありますし「確定」と「以下」が嚙み合わない矛盾もあります。全ての矛盾パターンになかなか気付くことができず、3回目の提出でようやく正解となりました。
自分の実装も良くなかったです。「確定」とか「以下」とかではなく、素直に「高橋君から推測できる値域」と「青木君から推測できる値域」を配列で管理していれば、矛盾の原因を区別しなくて済んだはず。
2017予選A C - Palindromic Matrix
問題へのリンク / 私の提出ソースコード
公式解説PDFを見るとなにやらテクニカルな解き方をしていますが、私は頭がよわよわなので素直に行列サイズの偶数奇数で処理を分岐させて頑張りました。26種類の文字のグループ分け(登場回数を4で割ったときのあまりによって4つのグループに分ける)をすればいいことに気づいてからは楽な気持ちで実装できました。
ところが提出してみると不正解。問題の意図は理解できていたのでテストケースの中身をチラ見することにし、それをヒントに原因を突き止めて(if文に書く条件式が不足してました)、2回目の提出で正解。
2017予選B C - 3 Steps
問題へのリンク / 私の提出ソースコード
グラフの問題でした。じっくり考えて、完全グラフになるときの答え $N(N-1)/2 - M$ には気づくことができましたが、完全グラフにならないときの答えがさっぱり分からず、諦めて公式解説PDFを読みました。
なるほど二部グラフ。二部グラフ自体は知っていましたが、今まで二部グラフを使って解く問題をAtCoderで見たことがなく(経験不足)、これを使うという発想には至りませんでした。
二部グラフかどうかの判定ロジックは、今回は自分の好きなBFSをチョイス(ちなみに "けんちょん本" ではDFSでやってます)。どうにか正解できました。
あとこれは余談ですがlong型にすべきところをint型にするというミスのせいで何回か不正解になりました。たまにやっちゃうんですよね。
2017予選C C - Inserting 'x'
問題へのリンク / 私の提出ソースコード
回文を作る問題です。文字列を前と後ろから同時に見ていって帳尻を合わせていきました。コーナーケースが多くてわりと緊張しましたが無事正解。
2018予選A C - 半分
問題へのリンク / 私の提出ソースコード
ついに来ました、本格的なDPの問題。DPは個人的に経験不足な分野です。
自力では方針を思いつかず、解説PDFを見ても漸化式の由来が説明省略されていたのでますます謎が深まるばかり。
とりあえず実際に、DPテーブルの具体例を図に描くことにしました。
例えば入力が
$3$ $10$
$8$ $32$ $2$
だとすると、$dp_{i,j,0}$($0$ がどこにもない数列の個数の数え上げ)は
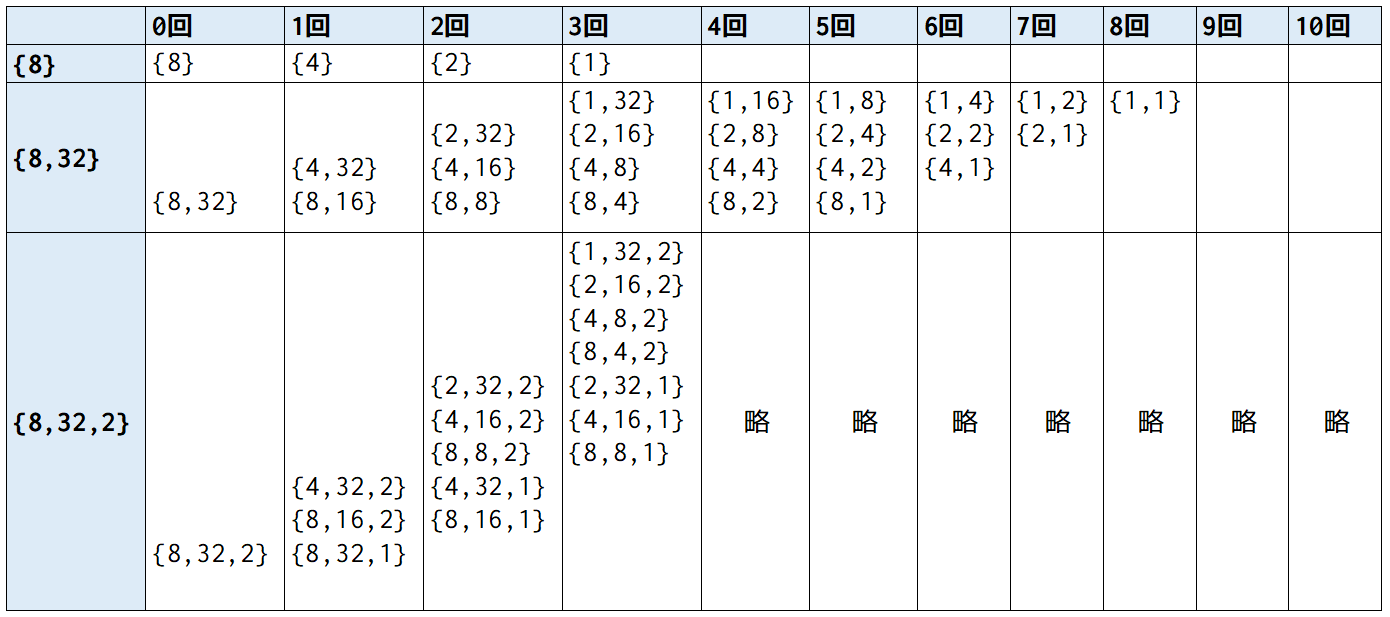
のようになり、$dp_{i,j,1}$($0$ がどこかにある数列の個数の数え上げ)は

のようになりました。このように自分で図を描くことで「一段下に進むと数列の個数はどうなるか」「一段上を見るときはどこまで左に遡ればいいか」「答えを出すには2枚のテーブルのどこを見ればいいか」といった規則性がだんだん見えてきました。
さらにこの問題を紹介しているブログ記事等をネットで探して読むことで、漸化式の由来を理解し、答えの出し方を理解し、ようやく正解できました。時間かかりました。難しかったです。
2018予選B C - Special Cake for CODE FESTIVAL
問題へのリンク / 私の提出ソースコード
C問題ラストはまさかの図形パズル。いわゆる「十字型のペントミノ」を隙間なく並べる問題と同じですね。
スプレーする法則はすぐに分かりましたが、最後に追加でスプレーする処理でコーナーケースをつぶしきれず不正解。二次元配列でちゃんと盤面を管理するようにプログラムをきれいに作り直しつつ、今度はきちんとコーナーケースを対処して正解。
以上で各コンテストのC問題もすべて正解となりました!
まとめ
A~Cの合計36問を解きましたが、いろいろなジャンルの問題があって楽しかったです。
問題によっては難しくて自力では解けなかったものもいくつかありましたが、解説を読むなどして理解を深め、最終的には正解ソースコードを提出することができたので良かったです。
勉強になりました!
おまけ
Qiitaのイベント「競技プログラミング研究月間 - みんなでさらなる高みを目指そう」で投稿された記事、いろいろ見てるだけで面白いです。
https://qiita.com/official-events/5a0502a2d94ed6a00c30
以上です。