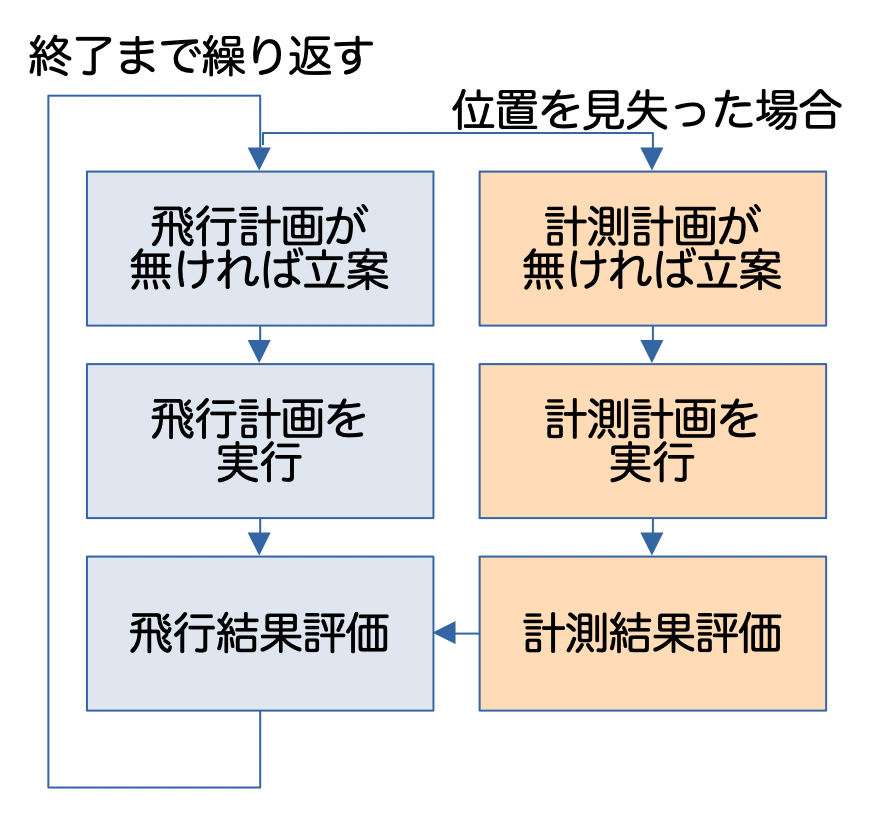
AtCoder第一回マスターズ選手権・決勝が、2024年3月20日に開催されました。チーム戦でのオンサイト大会という、AtCoderとしてはおそらく初めての形式で、大いに楽しめました。一方、チーム戦の決勝にふさわしい、難易度の高い問題が出題されました。
筆者は、比較的簡単なB問題を担当したのですが、決勝当日の時間ではやりきれなかったアイデアが多かったです。後日、時間をかけて実装し、本戦1位を超えるスコアを獲得しましたので、一歩一歩解き進める形で解説します。
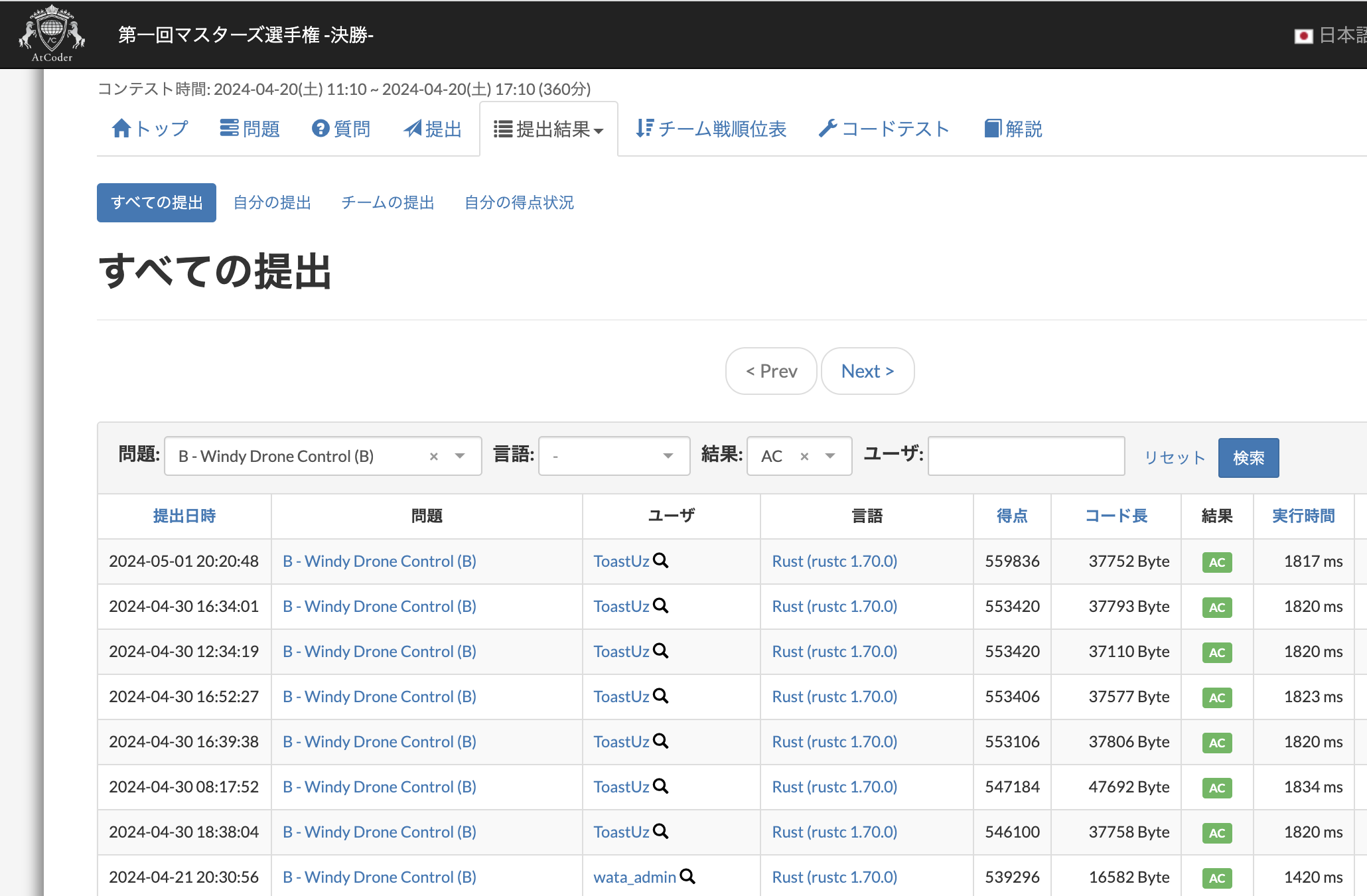
歴代1位となっている提出スコア(B問題の本戦1位は、525864点でした)
なお、ビジュアライザは公式提供されていませんので、チームメイトのzachさん提供のものを使っています。本記事でも大活躍です。
1. 問題
1.1. 問題概要
ドローンを操ることで、早く正確に10個の目標を巡る競争です。
- ステージによっては、壁があったり、風が吹いていたりして、行手を邪魔します
- ドローンの位置や速度を、直接知ることはできません
- 最大5000ターンの中で、各ターンで可能な操作は、2種類です
- 最大500の範囲で、加速度(っぽいもの)を指定する(風によって、速度は変わる)
- 方向を決めて壁までの距離を計測する(計測誤差がある)
- 目標の近辺に到達すると+1000点となりますが、壁に衝突すると-100点、各ターンごとに-2点となります
- 途中スコアの最大値が、そのステージのスコアとなります
問題は3種類あって、難易度が異なります。
| A問題 | B問題 | C問題 | |
|---|---|---|---|
| 壁 | なし | あり | あり |
| 風 | 強風 | 無風または微風 | 強風 |
| 計測誤差 | 大 | 小 | 大 |
なお、すべての問題で、エリアの端には固定の壁があります。
筆者は、もっとも簡単そうなB問題に取り組みました。
1.2. 問題分析
問題条件を分析することで、おおよその方針を得ることは、競技プログラミングの鉄則です。今回も、以下のように分析することができます。
- 位置と速度をステータスとして保持しつつ順次更新しながら、壁を避けて目標を巡るゲームである
- エリアの大きさ(20万×20万)に対して、壁はかなり疎な作りであるため、狭い経路を縫うような天才貪欲や、焼きなましやビームサーチ等のヒューリスティック典型は、使わなさそうである
- 特に無風の場合は、毎ターンの位置と速度は、幾何問題を解くことで決定できるため、「計測」は不要である
- 5000ターン経過した時の最大スコアは0点であるため、途中のターン(初期の推測としては1000ターン以下)までで最大値を獲得する必要がある(なお1000ターンで10目標完走だと8000点、500ターンだと9000点となる)
B問題は比較的簡単とはいえ、条件によって難易度が変わりますので、以下の順で解いていって、9000点を超えることを目標にします。
(1)無風かつ壁無し
(2)無風かつ壁あり
(3)微風
2. 無風
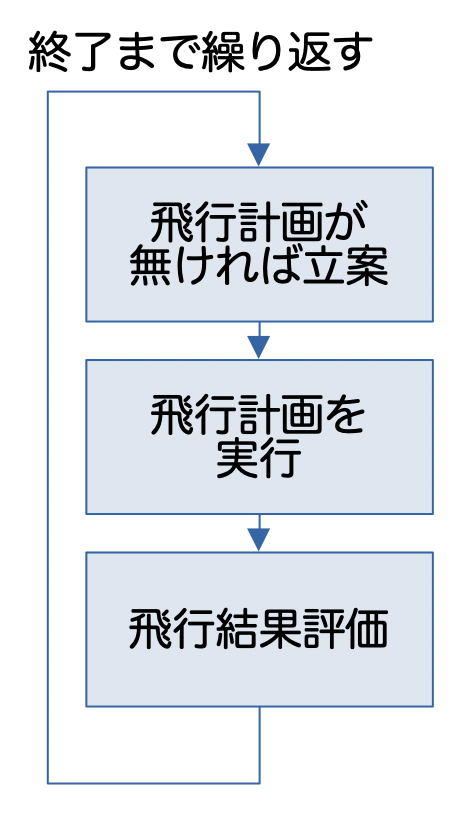
無風下では、飛行計画を立てて、その計画を実行し、評価する、というターンを繰り返します。壁が無い場合は、飛行計画は次の目標だけですが、壁がある場合は目標まで必ずしも直線で到達できないため、途中経路も考慮した複雑な飛行計画を立てる必要があります。
2.1. 壁無し+定速飛行
壁無しの場合は、最も近い目標を飛行計画に組み入れ、到達したら次に近い目標に変えていくという方法を試してみます。加速度の上限は500であるため、いつでも停止できるように、最大速度も500としておきます。
この方法でも7500点を超えることができましたので、目標を9000点にしたのは正しそうです。
B問題、Seed=2(無風)を、壁無しに変えたもの。Score=7504

2.2. 壁無し+アクセル
最大速度の制限を外してみます。当然、行き過ぎて壁にぶつかったり、大回りしたりしていますが、8500点近くになりました。なお、最大速度をチューニングすることで、より高い得点を得ることも可能ですが、さまざまなステージに適した最大速度を求めるのは難しいです。
B問題、Seed=2(無風)を、壁無しに変えたもの。Score=8490

2.3. 壁無し+アクセル+ブレーキ
最大速度をチューニングするのではなく、加速度の上限を守りつつ、目標に近づくにつれて順次速度を減らすようにしました。一定の力でブレーキをかけるようなものです。これにより、9500点を超えることができました。
B問題、Seed=2(無風)を、壁無しに変えたもの。Score=9590

どのくらいの強さでブレーキをかけるべきかは、以下のグラフから計算することが可能です。
階段上の面積が、最終的に進む距離に相当します。計算式で記述すると、以下のようになります。
\begin{align}
dist &= \frac{t (t + 1)}{2}A_{max} \\
(ただし、A_{max} &= 500, dist=目標までの距離) \\
\end{align}
これを $t$ について解くことで、ブレーキに必要な加速度が求められます。
\begin{align}
A_{next} &= V_{next} - V_{now} \\
&= A_{max} t - V_{now} \\
&= A_{max} \frac{-1 + \sqrt{ 1 + 8 dist / A_{max}}}{2} - V_{now} \\
(ただし、V_{now} &=現在の速度) \\
\end{align}
なお、厳密には端数の処理が必要ですが、あまり厳密すぎると逆に安定性が損なわれるようです。
2.4. 壁あり+飛行計画
次に、壁ありのパターンを攻略してみます。障害物を避けて目標に到達するために、途中経路も含めた飛行経過を立てる必要があります。
途中経路を求めるには、さまざまなグラフアルゴリズムが使えますが、こういった広大なエリアを効率よく探索するには、格子解法を使います。
暫定10位解法 RECRUIT 日本橋ハーフマラソン 2023冬(AHC018) 2. 複雑性を排する格子解法は典型です
次の目標までの経路を、格子解法を使って解いてみます。以下を工夫して、ダイクストラ法で途中経路も含めた飛行計画を決めるようにします。
- 荒過ぎず、細か過ぎず、といったちょうど良い格子サイズを決める
- 狭い場所を通れるようにするため、格子点以外に、壁の端(から少し先)の点も候補に加える
- 壁に近すぎる経路は衝突の危険があるため、壁に近い区間はペナルティを入れる
きれいに壁の間を縫って、次の目標まで辿り着くようになりました。しかし、格子点を順番に巡っているため、経路がガクガクしているとともに、速度が上がりません。
B問題、Seed=2(無風)、Score=7360 (長いので途中まで)

2.5. 飛行計画の先読み
飛行計画のかなり先でも直線で到達できるようであれば、途中経路をスキップするようにします。これによって、かなり滑らかに素早く飛行できるようになり、B問題無風で9000点を超えることができるようになりました。壁の有り無しにかかわらず、共通で使えるソルバーになりました。
3. 微風
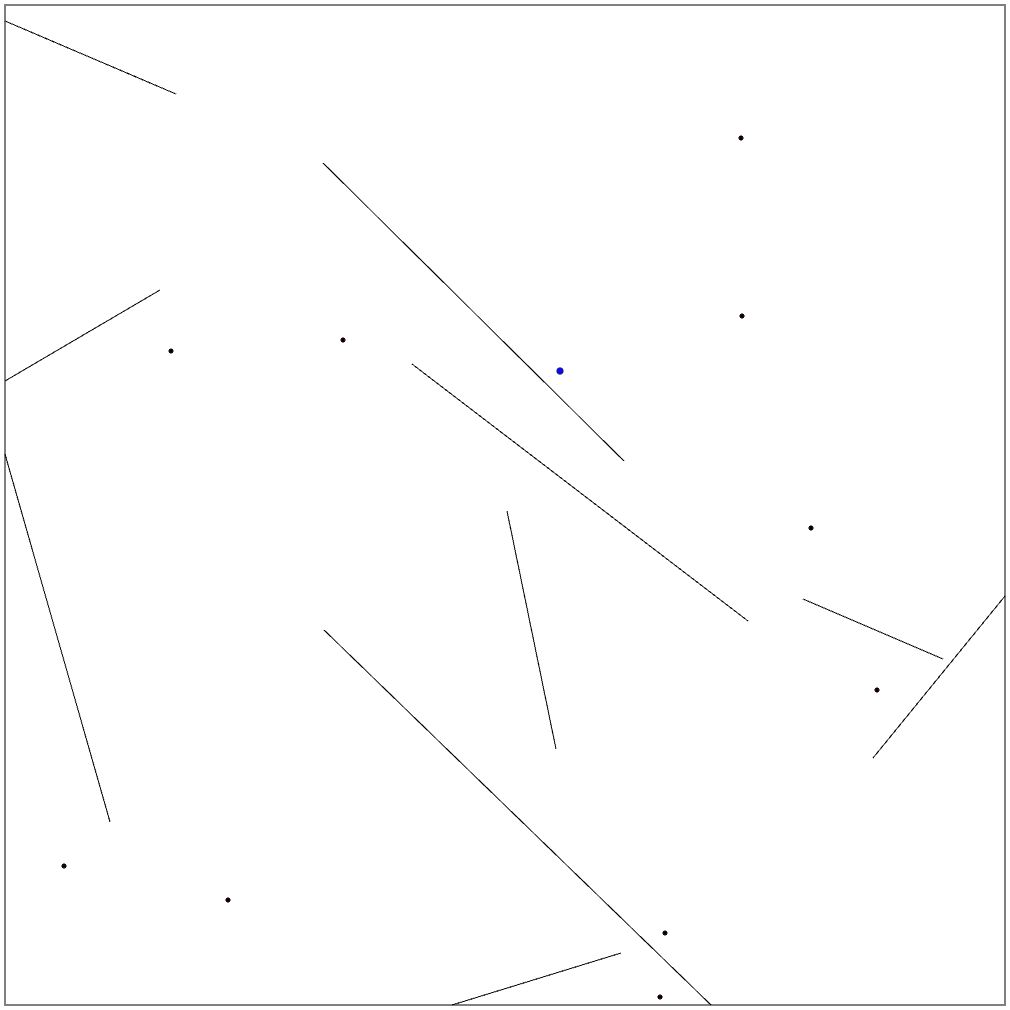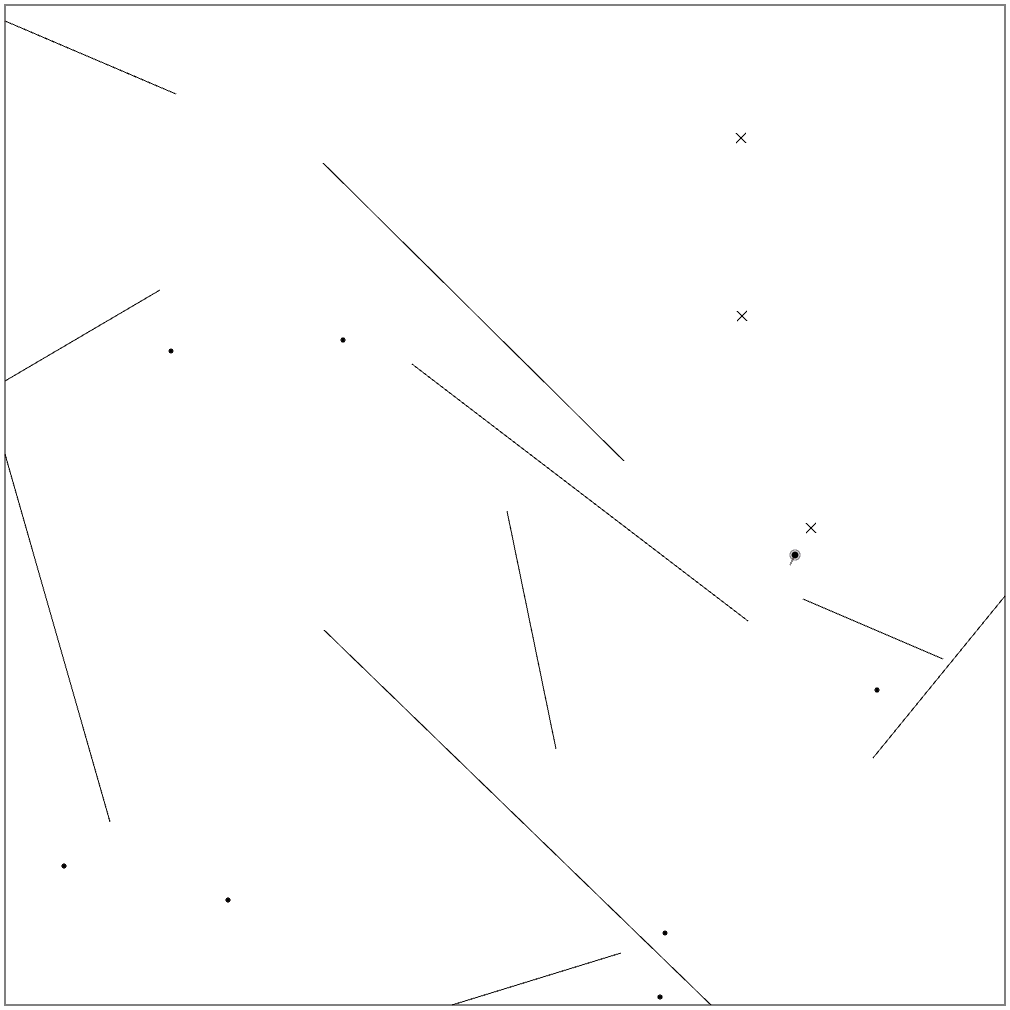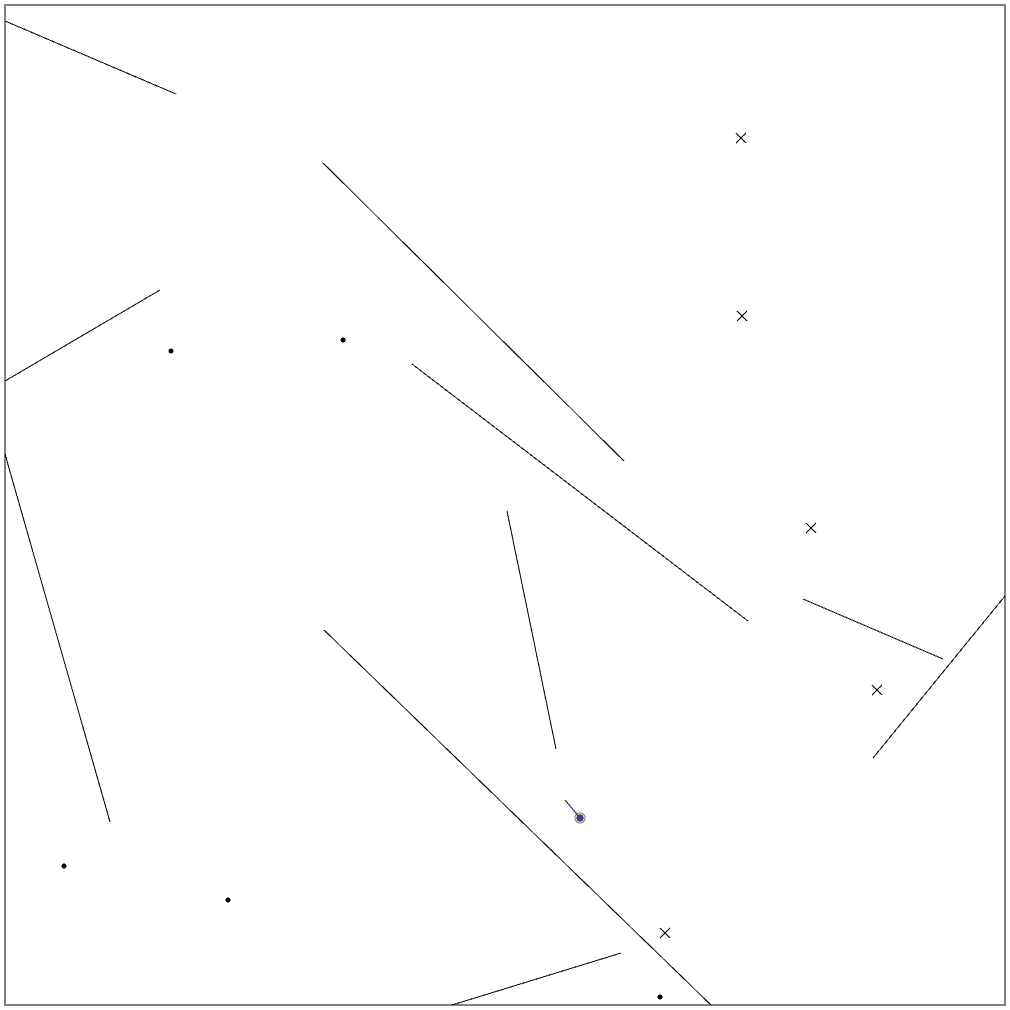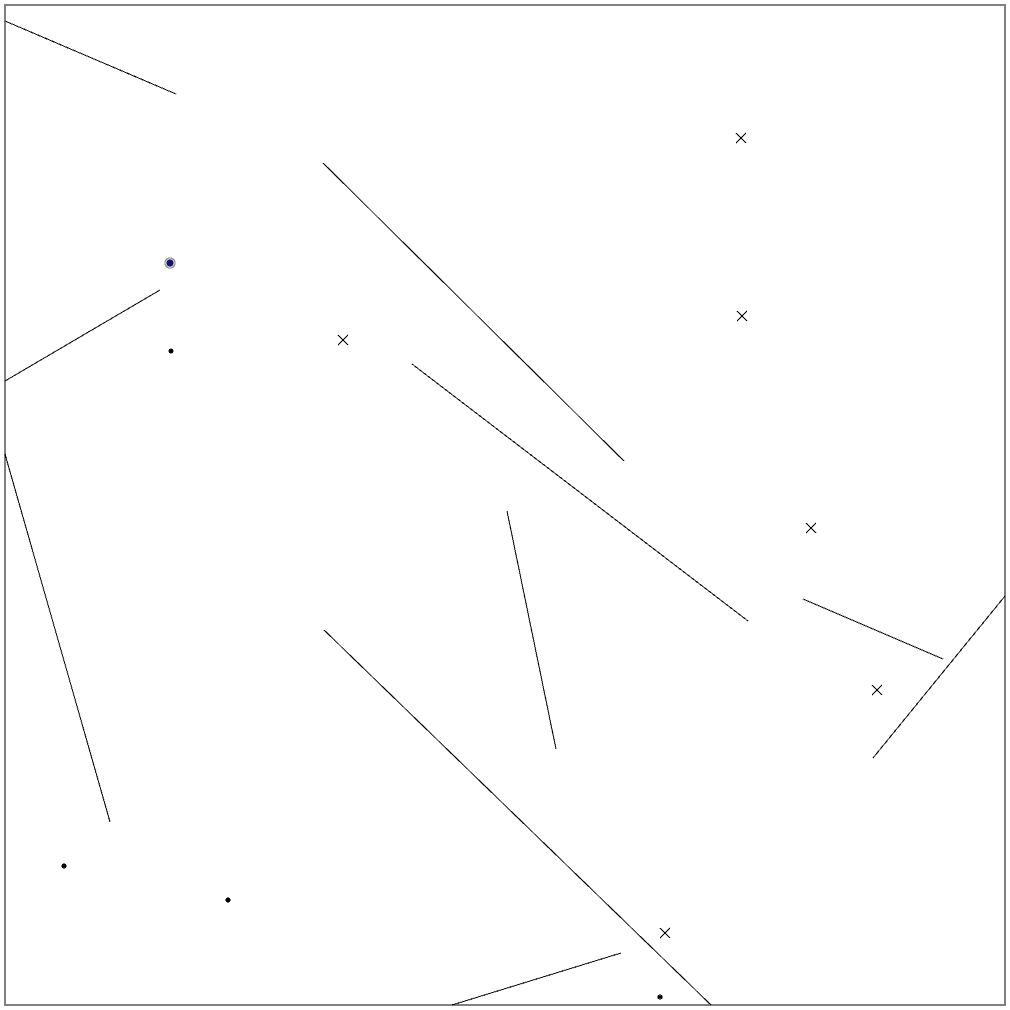
いよいよ、微風ステージの攻略です。これまでのアルゴリズムをそのまま適用しても、高得点を稼げるステージはありますが、かなり低い得点になってしまうステージも散見されます。Seed=4では3000点にいかない状況です。どうも、位置や速度に誤差が出るため、4番目の目標を見失っているようです。
3.1. 計測による位置補正
ここてはじめて、計測を使ってみます。目標地点の近くに来たはずなのに目標が無いなど、位置を見失った時に計測を行います。そして、現在のステータスで本来得られる計測結果(予測値)と、実際の計測結果(真値)との誤差をもとに、位置や速度を補正します。
なお、微風下では、位置のみ補正して速度は補正しない戦略が良いようです。
$i$ ターン目の加速度誤差を確率変数 $X_i$ として表すと、各 $X_i$ は独立です。また、微風条件とは、加速度誤差の分散が常に $V[X_i] = 1$ ということです。この時、$n$ ターン目の速度の誤差成分 $Y_n$ は、 $ Y_n = \sum_{i=1}^{n} X_i $ であるため、分散の和の公式により、$ V[Y_n] = \sum_{i=1}^{n} V[X_i] =n$ となります。すなわち、速度の標準偏差は、500ターン経過しても $ \sqrt{500} \fallingdotseq 22.4 $ にしかなりません。
同様に、$n$ ターン目の位置の誤差成分 $Z_n$ は、
\begin{align}
Z_n &= \sum_{i=1}^{n}Y_i \\
&= \sum_{i=1}^{n}\sum_{j=1}^{i} X_j \\
&= \sum_{i=1}^{n} (n - i + 1)X_i \\
\end{align}
であるため、分散の和の公式により、
\begin{align}
V[Z_n] &= \sum_{i=1}^{n} (n - i + 1)^2 V[X_i] \\
&= \sum_{i=1}^{n} (n - i + 1)^2 \\
&= \sum_{i=1}^{n} i^2 \\
&= \frac{n(n+1)(2n+1)}{6} \\
\end{align}
となります。すなわち、位置の標準偏差は、500ターン経過すると $ \sqrt{41,791,750} \fallingdotseq 6,465 $ にもなり、補正の必要性が高いということがわかります。ここで、 $Y_i$ は互いに従属なので、 $ V[Z_n] = \sum_{i=1}^{n} V[Y_i]$ は成り立たないことに、注意してください。
なお、必ずしもこういう解析的計算ができる(思いつく)とは限りませんので、モンテカルロ法のような手段で近似値を得ることは有効です。
結果として位置を微妙に補正しつつ目標を次々にクリアできるようになりました。しかしながら、7番目の目標を見失っているようです。上方向の計測が、ちょうど壁の端にかかるため、予測値と真値との差が安定しないためです。これ以外に、計測方向と壁の方向が平行に近い時も、計測が安定しないようです。
3.2. 計測の安定化 = 完成
以下のような手段で、計測の安定化を図ります。
- 現在の推定位置が少しズレただけで計測先の壁を外してしまう場合に計測結果が推定と大きく変わってしまうことがあるため、あらかじめ推定位置を上下左右にずらすことで候補を増やし、計測結果をもとに候補の中から起点となる推定位置を最適に選択する
- 計測をなるべく短距離にするとともに、位置のズレが計測結果に大きな影響を与えすぎないように、固定方向(上下左右)ではなく、壁に対して垂直方向に計測する
- 計測誤差が大きくなりやすい長い計測距離になる場合は、計測方向として選択する壁の優先度を下げる
- どうしても長い計測距離を選択せざるをえない場合は、計測誤差を考慮して複数回の計測を行う
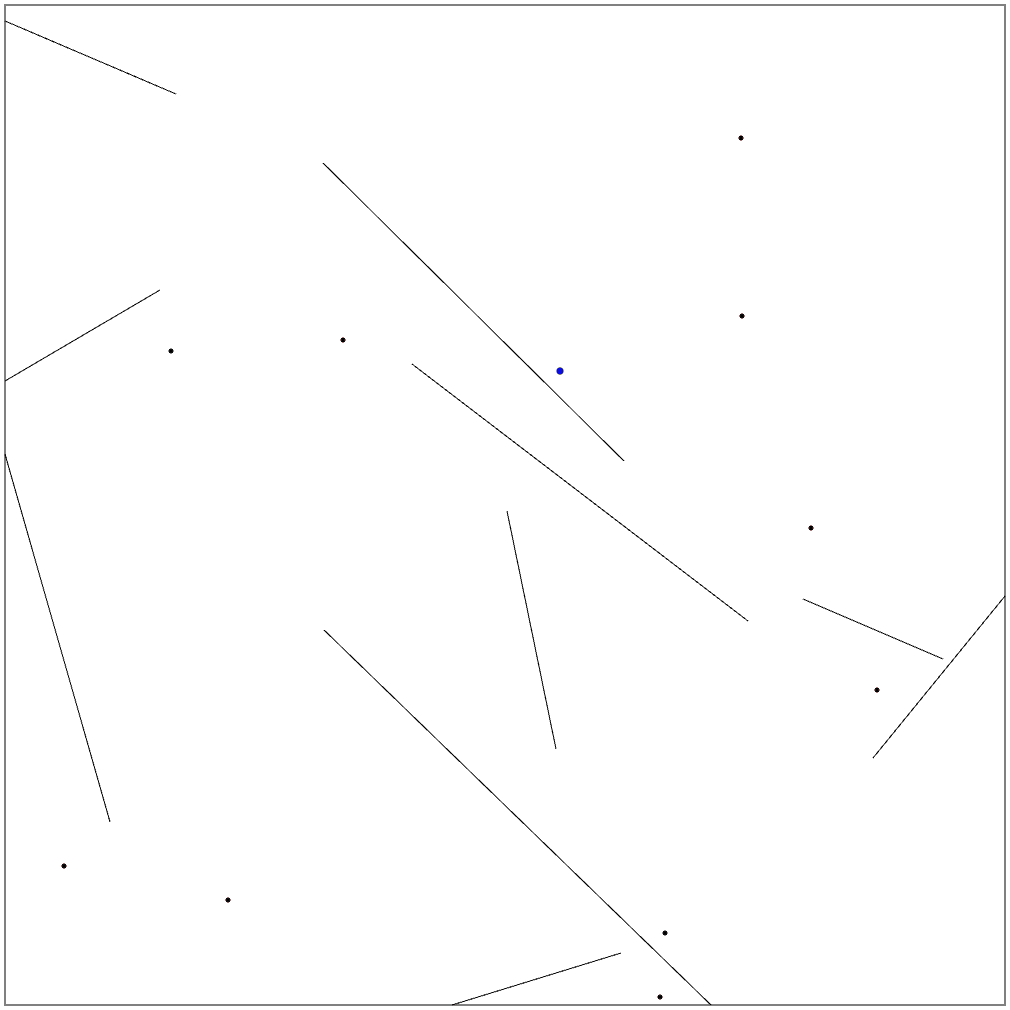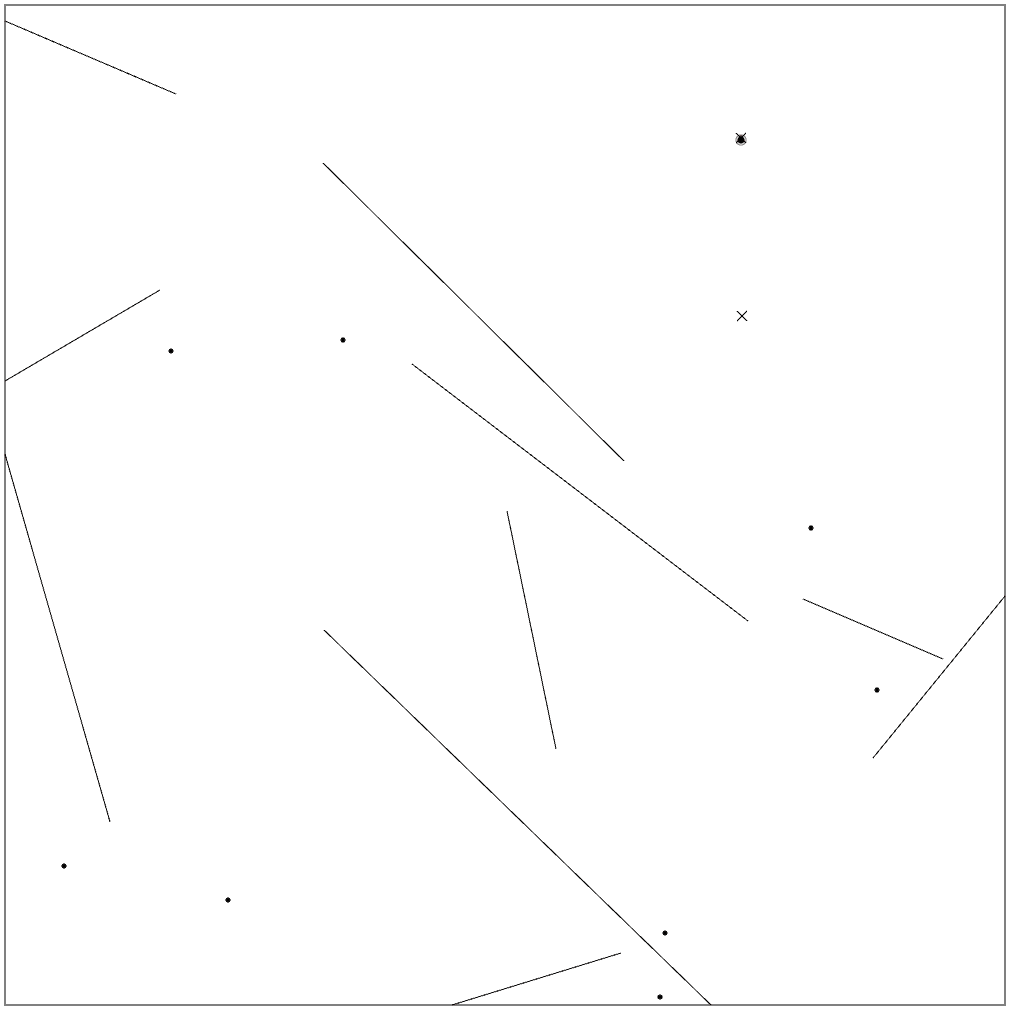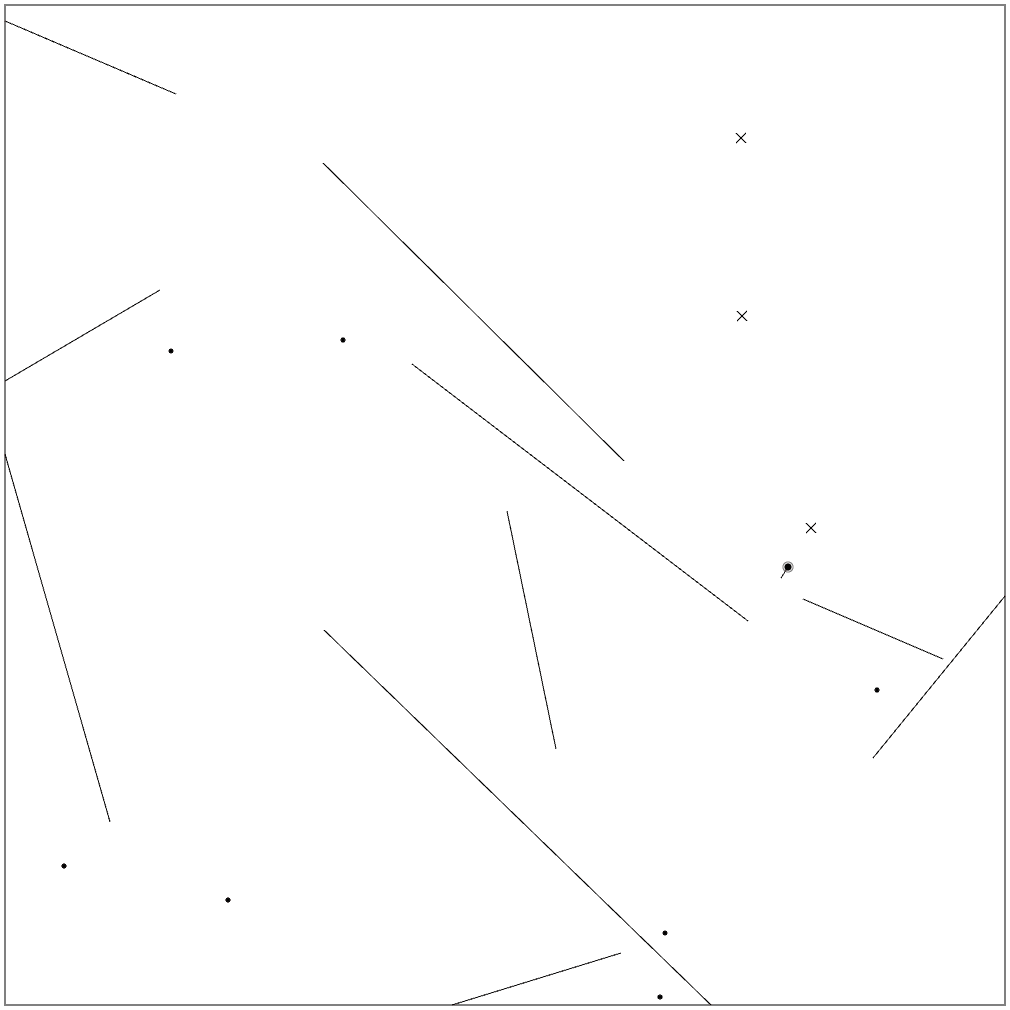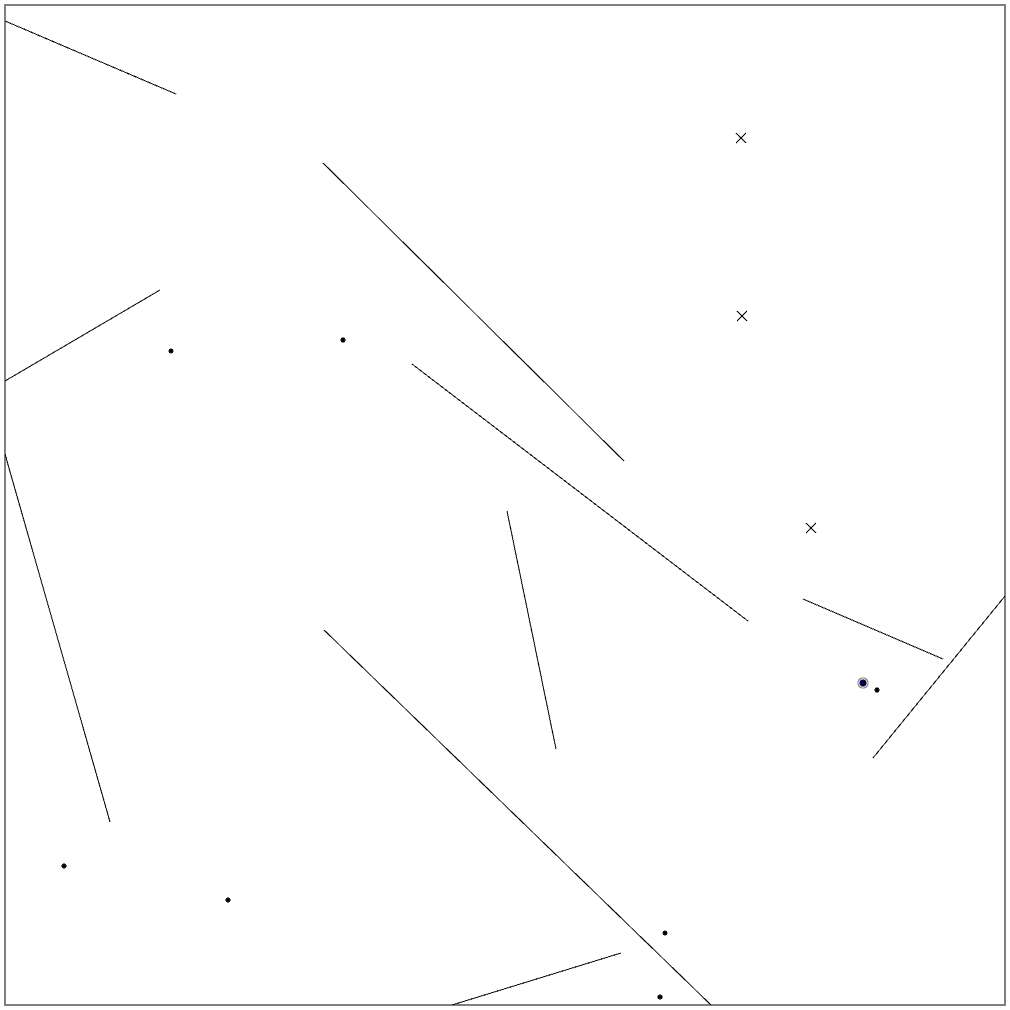
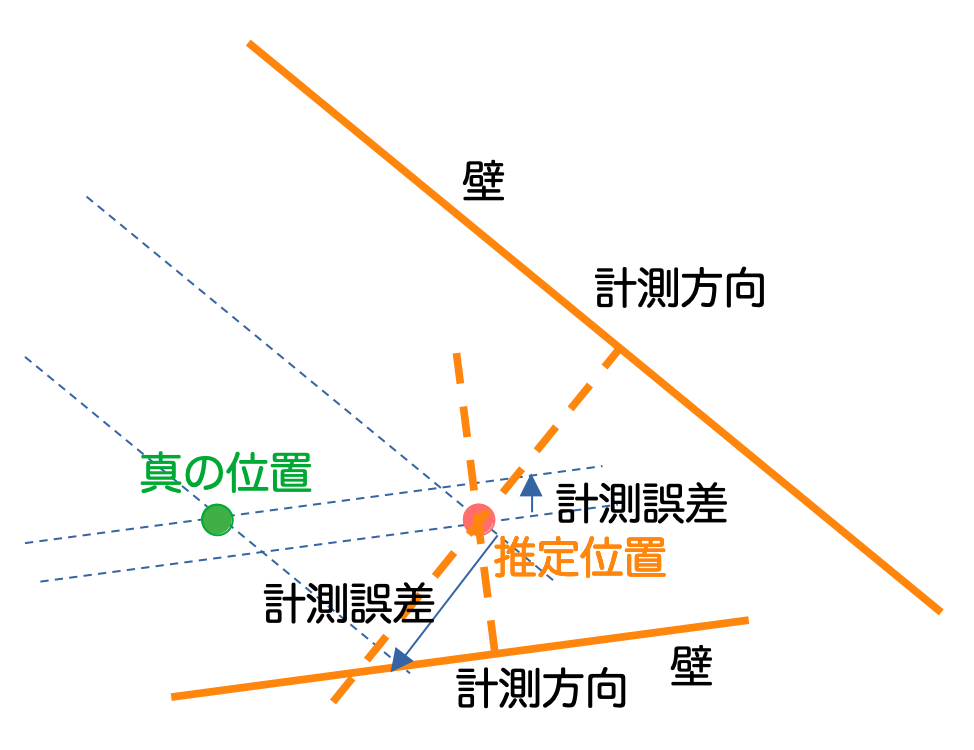
壁に対して垂直方向に計測する、ということは、複数の計測方向が必ずしも直交していないことになります。この場合、真の位置と推定位置の誤差は、必ずしも計測誤差ベクトルの和にはならないことに注意してください。以下の図を見ると、かなり外れたところに真の位置があると、わかります。
真の位置を解析的に求める方法を示します。
推定位置ベクトルを $x$ 、真の位置ベクトルを $y$ 、計測誤差ベクトルを $d_1, d_2$ 、計測誤差ベクトルの垂直となるベクトルを $\hat{d}_1, \hat{d}_2$ とすると、$s, t$ を実数として、
$$ y = x + {d}_1 - s\hat{d}_1 = x + {d}_2 + t\hat{d}_2 $$
が成り立ちます(計算に便利なように$s$にはマイナスをつけていますが、実数なので問題ありません)。すなわち、
$${d}_1 - s\hat{d}_1 = {d}_2 + t\hat{d}_2 $$
となります。これは、 $d1$ と $d2$ が平行ではない時に、行列の式
\begin{pmatrix}
\hat{d}_1 & \hat{d}_2
\end{pmatrix}
\begin{pmatrix}
s \\
t \\
\end{pmatrix}
= d_1 - d_2
を解くことで求められます。
以上により、微風下でも9000点を超えるようになりました。細かいズレをすぐに見つけて、正しく補正している様子が、わかるでしょう。
B問題、Seed=4(微風)、Score=9436
この問題のみ、Zachさんのビジュアライザの最新版を使ってみました。予測とのズレ具合や、計測の様子もわかります。

4. 終わりに
実際の決勝大会本戦では、このような落ち着いたステップで解き進めることはできず、無風かつ壁あり前提で、2.1と2.4を実装しただけです。それでも、まずまずの成績でしたので、短時間に解くことがいかに難しいことかがわかります。
素晴らしい大会を準備・盛り上げていただいた、すべての大会関係者、予選を含めた競技者、チームメイトに、感謝を申し上げます。対戦ありがとうございました。