Python+Optunaで952億点 AHC003を深層学習ノウハウで攻略

AtCoder Heuristic Contest 003 (AHC003)を、Python+Optunaを使った深層学習のノウハウで、（点数そのものは大したことはありませんが）952億点出しました。手法を解説します。

2021/5/31追記: システムテストで98位と二桁順位に入りました！ お疲れさまでした。

参考: AtCoder Heuristic Contest 003

AHCは、AtCoderが主催する競技プログラミングの一種です。正解が必ずしも求められない問題について、数時間〜1週間で、どこまで最適解に近づけられるかを争う競技です。

1. AHC003の概要

30 × 30という比較的小さな離散平面における最短経路を求める問題です。ただし、コスト情報は隠蔽されており、最短と考える経路をクエリーし得られた経路コストを元に、推測する必要があります。また得られる経路コストにはノイズが乗っており、コスト情報の推測は一筋縄ではいきません。

1000回のクエリーのトータルでの、真の最短経路との近さが得点となります。また、後の方のクエリーほど、得点に占める割合が大きくなってきます。よって、初期のクエリーはあえて捨てて、コスト情報の推測のためのデータ集めを優先するといった、戦略性の高い競技になっています。

2. 深層学習の応用

深層学習は、ざっくりと言うと、説明変数となる入力データを、最適と思われるモデルに通すことで、得られた目的変数となる出力データと、正解データとの誤差を、最小化するように、少しずつモデルを修正していくものです。その際、モデルを多層構造で定義することから「深層学習」と呼びます。

2.1. モデル

通常の深層学習では、説明変数が与えられて、モデルの形（層と層を結びつける計算のウエイトや、各層の数式）を最適化します。ところじ、今回の問題は、モデルの形が与えられていて、説明変数を推測するという特徴があります。具体的には、インタラクティブに得られる目的変数の正解データをもとに、モデルの真の説明変数を推測していきます。

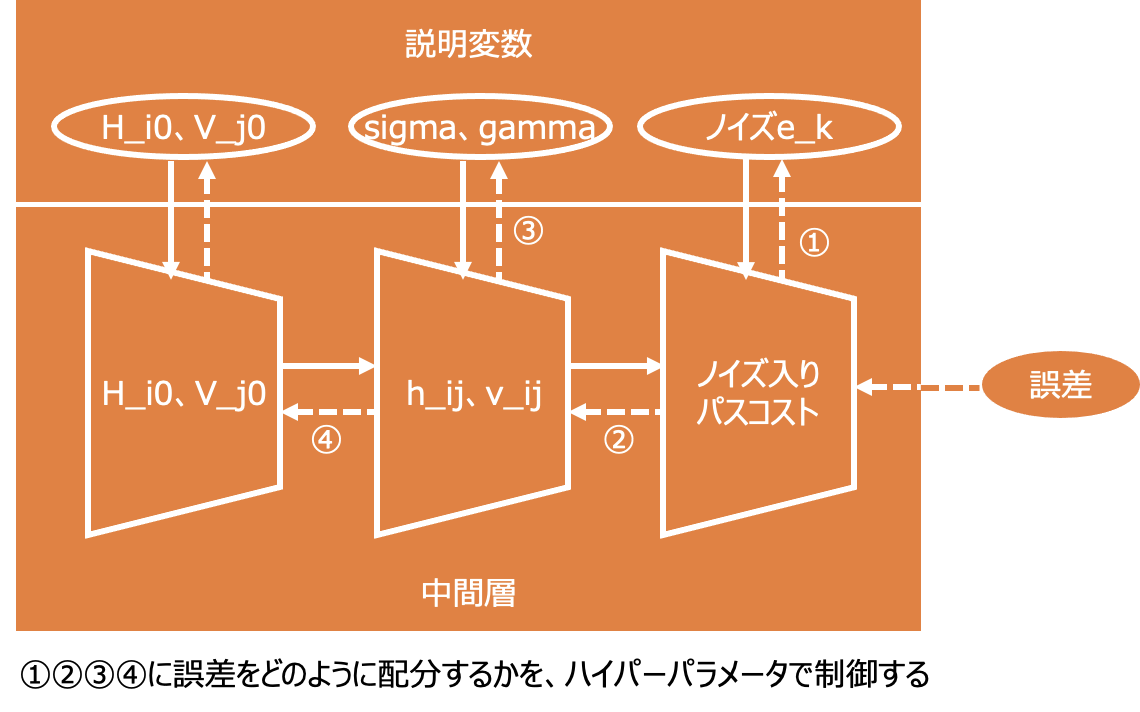
よって、モデルの形を忠実に再現しつつ、インタラクティブに得られた誤差情報をもとに、初期値として与えた（推測した）説明変数を最適化していく戦略をとります。下図にイメージを表します。

2.2. 誤差逆伝播

モデルの形が与えられているため、誤差逆伝播についても、モデルを逆から巻もどしていき、推測した説明変数ごとの誤差を分解していきます。ただし、足し算の結果を元に戻せないように、今回のモデルも一意的に巻き戻すことはできません。

もともと、深層学習においても、誤差逆伝播の「感度」は「学習率」というハイパーパラメータで制御されます。よって、今回の問題でも、各層の巻き戻し程度やその配分を、ハイパーパラメータで調整できるようにします。

誤差逆伝搬で最適化する対象ではないが、各種の深層学習の動作を規定するのに必要なパラメータを、ハイパーパラメータと呼びます。

この際、モデル定義としては、乱数を使いつつもD値といったパラメータで順方向の計算が定義されていますので、逆方向の分解においても、その定義をなるべく尊重することで、最適化の効率がアップします。なお、実際のモデル定義はさらに複雑なのですが、速度と精度のバランスを考慮して、ある程度の枝葉は考慮から外す必要があります。

C++などを使って枝葉も精緻かつ高速にモデル表現できると、もう一段、点数が伸びたかと思います。

ここまでで、940億点くらいは達成できました。

2.3. ハイパーパラメータの最適化

さらに、ハイパーパラメータそのものを、得られた最終スコアをもとに、最適化していきます。ハイパーパラメータは、モデルを推論させる提出プログラムの外側のインタラクティブテスタ側で、最適化することが可能です。そのため、最適化にいくらでも時間を使うことができます。

ハイパーパラメータの最適化のツールとしては、optunaがメジャーです。一直線に最適化をするのではなく、時々は傾向に無い組合せを試してみて、局所最適に陥っていないかを確かめるような動きをします。

以下は、optuna dashboardの画面です。

ここまでで、テスト環境では956億点くらいになりました。

2.4. バリデーション

深層学習につきものなのが、過学習によって汎化性能が出ない可能性です。すなわち、手元のテストでは高得点を達成していても、それは手元のテストケースに過剰に最適化された結果であり、実際に提出したスコアの得点が伸びない可能性があります。よって、一般的な深層学習では、学習データだけでなく、検証データやテストデータなどによって、過学習していないかを判定するようにしています。

今回の競技では、自分でテストケースを大量に生成することが可能です。よって、そこから検証データやテストデータを得ること可能なばかりか、大量の学習データを使って学習させることで、過学習を防止することも可能です。しかし、それには多大なコンピューティングパワーと時間を消費してしまいます。

よって、AtCoderで用意している暫定テストの得点を見ることで、得られた結果が過学習をしていないかを確認するようにします。結果としては、4億点分くらい過学習しているように見えますが、手元のテストの得点が伸びることで暫定テストの得点も伸びるため、許容範囲としました。最終的には、自分の暫定テストの最高値であった、952億点でのモデルとハイパーパラメータを提出しました。

3. コーディングにおけるポイント

最後にコーディングにおけるポイントを箇条書きします。インタラクティブ型問題は、テスタ側のコードがもともと特殊です。今回はさらにそれをoptumaと複合させているため、ググっても参考例があまり無いコードに仕上がっています。

以下にポイントを記載します。コードのコメントにも情報ありますので、そちらも参照ください。

3.1. インタラクティブテスタ

• インタラクティブテスタそのものはoptunaを使うためPython3.8で記述しています。ただし、optunaの部分以外は、AtCoderのPyPy3（標準ライブラリのみ）で通るコードにしています。
• テスト対象プログラムはsubprocessを使って起動します。さらに、インタラクティブに会話するには、PopenとPIPEを使う必要があります。
• ハイパーパラメータの流し込みは、テスト対象プログラムの起動時のコマンドラインオプションで実現します。ハイパーパラメータを辞書として管理しておくと、流し込みが容易です。
• optunaの部分は非常に基礎的な記述かつ記述量も少ないため、コードを読むことで、理解できるでしょう。なお、ダッシュボードで分析したり、途中で最適化を中断・再開できるように、ストレージ保存を利用することが望ましいです。
• 問題そのもので与えられた変数名はそのまま利用し、その他のモジュール名や変数名は、optunaの流儀に従いました。

3.2. テスト対象プログラム

• テスト対象プログラムはそのまま提出するとともに、実際のAtCoderでの実行時間と近似させる必要があるため、PyPy3（標準ライブラリのみ）で動作させています。
• ハイパーパラメータの受け取りは、Pythonの闇（笑）であるexecで行います。
• ハイパーパラメータのグローバル初期値を、提出時のハイパーパラメータとします。これにより、テスト対象プログラムをそのまま提出でき、便利です。
• 初期の最適パスについては、必ずしも、ダイクストラ法による最適探索をしないほうがよいかもしれません。初期は全体への点数寄与が相対的に少ないですので、少し暴れることで、パラメータ空間の全体像を知る方が有益です。よって、バッチでの初期探索→バッチでの最適化→少しずつ最適パス探索と最適化を混在、という戦略にしています。queryモジュールのsearch_algorismを切り替えることで、最適化アルゴリズムを切り替えるしくみにしています。
• TLEを避けつつ時間いっぱいを有効に使うため、細かく時間制御をして、遅れていることを検知したら最適化をスキップするようにしています。
• 問題そのもので与えられた変数名はそのまま利用し、その他のモジュール名や変数名は、深層学習の流儀に従いました。

4. コード

最後に、インタラクティブテスタおよびテスト対象プログラムの全体を示します。

##4.1. インタラクティブテスタ

import time
import subprocess
import optuna

INF = 10 ** 16

# テスト対象プログラムと会話する
def talk(cp, si, sj, ti, tj, prev_result):
    _INPUT = ''
    if prev_result > 0:
        _INPUT = f'{prev_result}\n'
    if not (si == sj == ti == tj == 0):
        _INPUT += f'{si} {sj} {ti} {tj}\n'
    cp.stdin.write(_INPUT)
    cp.stdin.flush()
    res = ''
    if not si == sj == ti == tj == 0:
        res = cp.stdout.readline()[:-1]
    return res

# 1回分の正解データをもとに、一連のルートについてテスト対象プログラムを評価する
def objective_sub(filename, **kwargs):
    # ハイパーパラメータをコマンドラインに設定する
    cmd = 'pypy3 ahc003.py'
    cmd += ''.join([f' -{k}={v}' for k, v in kwargs.items()])
    with open(filename) as f:
        lines = f.readlines()

    V = H = 30
    N = 1000

    # 正解データをセットする
    h_ij = [list(map(int, lines[n][:-1].split())) for n in range(V)]
    v_ij = [list(map(int, lines[V+n][:-1].split())) for n in range(V-1)]
    lines = lines[2 * V - 1:]

    DIRS = {'U': (-1, 0), 'D': (1, 0), 'L': (0, -1), 'R': (0, 1)}

    # テスト対象プログラムを起動する
    cp = subprocess.Popen(cmd, stdin=subprocess.PIPE, stdout=subprocess.PIPE, shell=True, text=True)
    stime = time.time()

    # パスの長さと正しさを評価 
    def compute_path_length(i, j, ti, tj, dirs):
        res = 0
        for d in dirs:
            di, dj = DIRS[d]
            ii, jj = i + di, j + dj
            if di != 0:
                res += v_ij[min(i, ii)][j]
            else:
                res += h_ij[i][min(j, jj)]
            i, j = ii, jj
        return (i == ti) & (j == tj), res

    prev_result = 0
    score = 0

    # 問題を順次読み込んでテストする
    for i, line in enumerate(lines):
        si, sj, ti, tj, a, e_k = line[:-1].split()
        si, sj, ti, tj, a = map(int, (si, sj, ti, tj, a))
        e_k = float(e_k)
        path = talk(cp, si, sj, ti, tj, prev_result)
        ok, b = compute_path_length(si, sj, ti, tj, path)
        if not ok:
            score = 0
            break
        score = score * 0.998 + a / b
        prev_result = round(b * e_k)

    talk(cp, 0, 0, 0, 0, prev_result)
    score = round(2312311 * score)
    # TLEになっていないかを検証するために計算に使った時間も返す
    return score, time.time() - stime

# すべての正解データをもとに、テスト対象プログラムを評価する
def objective(trial):
    # ハイパーパラメータの探索範囲を定義
    # ※最終提出値を得た時の探索範囲とは異なります
    params = {
        'N0': trial.suggest_int('N0', 0, 50, 5),
        'epochs0': trial.suggest_int('epochs0', 0, 100, 5),
        'lr0': trial.suggest_float('lr0', 0., 1., step=0.02),
        'lr1': trial.suggest_float('lr1', 0., 1., step=0.02),
        'lr_n0': trial.suggest_float('lr_n0', 0., 0.05, step=0.005),
        'lr_n1': trial.suggest_float('lr_n1', 0., 0.05, step=0.005),
        'D': trial.suggest_int('D', 100, 3000, 50),
    }

    import glob
    total_score = 0
    max_time = 0
    # 正解データのファイルがあるだけ評価を繰り返す
    filenames = glob.glob('tools/in/*.txt')
    for filename in sorted(filenames):
        score, resp_time = objective_sub(filename, **params)
        print(filename.split('/')[-1], score, resp_time)
        total_score += score
        max_time = max(max_time, resp_time)
    print('total:', total_score, 'max_time:', max_time)
    # 時間を後から参照可能にするために、attrに登録しておく
    trial.set_user_attr("max_time", max_time)
    # 評価値の最小方向に最適化するためマイナスで返す
    # create_studyのオプションで最大方向の最適化にすることも可能
    return -total_score * 100 // len(filenames)

def main():
    # optunaの学習指示
    study = optuna.create_study(
        study_name='ahc003-2021052903',
        storage='sqlite:///./ahc003.db', load_if_exists=True)
    study.optimize(objective, n_trials=1000)

if __name__ == '__main__':
    main()

4.2. テスト対象プログラム

import sys
import heapq
import time

stime = time.time()
expired = lambda x: time.time() - stime > x 

refresh_period = 10

# ハイパーパラメータのデフォルト値（optunaで鍛えた最適値）※最終提出値とは異なります
N0 = 50
epochs0 = 0
lr0, lr1 = 0.04, 0.2
lr_n0, lr_n1 = 0.01, 0.015
D = 1050

def main():
    # コマンドラインからのハイパーパラメータ読み込み（学習時のみ）
    args = sys.argv
    for arg in args[1:]:
        if arg[0] == '-':
            exec(arg[1:], globals())

    # なるべく忠実に問題文の条件を再現
    # ただし、M=2のパターンは再現しても重くなるだけなので避ける
    # その代わりoptunaでのDの上限を問題文より緩和しておく
    V = H = 30
    N = 1000

    V_j0 = [5000] * H
    H_i0 = [5000] * V
    sigma = [[0] * (H - 1) for _ in range(V)]
    gamma = [[0] * H for _ in range(V - 1)]
    e_k = [1] * N

    # 問題文の条件に基づいて計算される、「辺」のコスト
    h_ij = [[5000] * (H - 1) for _ in range(V)]
    v_ij = [[5000] * H for _ in range(V - 1)]

    DIRS = {'U': (-1, 0), 'D': (1, 0), 'L': (0, -1), 'R': (0, 1)}
    INF = 10 ** 16

    history = []

    # 辺のコスト計算
    def calc_cost():
        nonlocal h_ij
        nonlocal v_ij
        h_ij = [[sigma[i][j] + H_i0[i] for j in range(H - 1)] for i in range(V)]
        v_ij = [[gamma[i][j] + V_j0[j] for j in range(H)] for i in range(V - 1)]

    # 初期の単純ルート探索
    def simple_route(si, sj, ti, tj):
        di, dj = ti - si, tj - sj
        adi, adj = abs(di), abs(dj)
        path_i = ('D' if di > 0 else 'U') * adi
        path_j = ('R' if dj > 0 else 'L') * adj
        if adi > adj:
            return path_i + path_j
        else:
            return path_j + path_i

    # ダイクストラ法による最適ルート探索
    def best_route(si, sj, ti, tj):
        distances = [[INF] * H for _ in range(V)]
        distances[si][sj] = 0
        q = []
        heapq.heappush(q, (0, si, sj, ''))
        while len(q) > 0:
            distance, i, j, path = heapq.heappop(q)
            if (i, j) == (ti, tj):
                return path
            for name, d in DIRS.items():   # 隣接候補
                di, dj = d
                ii, jj = i + di, j + dj
                if ii < 0 or ii >= V or jj < 0 or jj >= H:
                    continue
                if di != 0:
                    cost = v_ij[min(i, ii)][j]
                else:
                    cost = h_ij[i][min(j, jj)]
                new_distance = distance + cost
                if new_distance < distances[ii][jj]:
                    distances[ii][jj] = new_distance   # 最短距離を更新
                    heapq.heappush(q, (new_distance, ii, jj, path + name))   # 最短距離をヒープキューで管理
        assert False

    # 探索結果と与えられたtrue値から、パラメータをチューニングする
    def optimizer(i, j, path, true, pred, lr):
        for d in path:
            di, dj = DIRS[d]
            ii, jj = i + di, j + dj
            # (真値 - 予測値の差) × パスの構成要素の比重 = ギャップ
            gap = int((true - pred) / len(path) * lr)
            # ギャップを（なんちゃって）誤差逆伝搬する
            if di == 0:
                jm = min(j, jj)
                sigma[i][jm] += gap
                gap2 = sigma[i][jm] - max(-D, min(D, sigma[i][jm]))
                sigma[i][jm] -= gap2
                H_i0[i] += gap2
                H_i0[i] = max(1000 + D, min(9000 - D, H_i0[i]))
            else:
                im = min(i, ii)
                gamma[im][j] += gap
                gap2 = gamma[im][j] - max(-D, min(D, gamma[im][j]))
                gamma[im][j] -= gap2
                V_j0[j] += gap2
                V_j0[j] = max(1000 + D, min(9000 - D, V_j0[j]))
            i, j = ii, jj 

    # 探索結果のルートコストを現在のパラチメータをもとに計算して「予測値」を出す
    def predict(i, j, path):
        res = 0
        for d in path:
            di, dj = DIRS[d]
            ii, jj = i + di, j + dj
            if di == 0:
                res += h_ij[i][min(j, jj)]
            else:
                res += v_ij[min(i, ii)][j]
            i, j = ii, jj 
        return res

    # 過去履歴をもとに、1エポック分の学習をする
    def fit(lr=0.1, lr_n=0.5):
        global v_ij
        global h_ij
        for n, (true, si, sj, path) in enumerate(history):
            pred = predict(si, sj, path)
            # 真値をノイズ補正しておく
            e_k[n] = max(0.9, min(1.1, e_k[n] + (true / pred - e_k[n]) * lr_n))
            true2 = true / e_k[n]
            optimizer(si, sj, path, true2, pred, lr)
            calc_cost()
        return

    # 一連のクエリーと外部システムとの入出力
    def query(search_algorism):
        si, sj, ti, tj = map(int, input().split())
        path = search_algorism(si, sj, ti, tj)
        print(path, flush=True)
        true = int(input())
        history.append((true, si, sj, path))

    # 以上のモジュールを、ハイパーパラメータをもとに、時間経過を考慮して組み合わせる
    correction = max(0, 100 - N0) / 100  # TLE防止の補正
    for _ in range(N0):
        query(simple_route)
    for epoch in range(epochs0):
        fit(lr=lr0, lr_n=lr_n0)
        if expired(1.0 - correction * 0.9):
            break
    for n in range(N0, N):
        if n % refresh_period == 0 and not expired(1.9 - (N - n) * 0.0007 - correction * 0.1):
            fit(lr=lr1, lr_n=lr_n1)
        query(best_route)

if __name__ == '__main__':
    main()