Atcoder ABC115 過去問演習

#はじめに
過去問である ABC115 の勉強メモです。
使用言語は Python です。

#A - Christmas Eve Eve Eve
Difficulty : 0
if 文で分岐を書くのが一番わかりやすく安定していると思います。

d = int(input())
if d == 22:
    print('Christmas Eve Eve Eve')
if d == 23:
    print('Christmas Eve Eve')
if d == 24:
    print('Christmas Eve')
if d == 25:
    print('Christmas')

#B - Christmas Eve Eve
Difficulty : 24
まず、割引なしの場合の値段の合計を求めます。
そこから、一番高い品物の半額の値段を引くと支払い金額になります。

n = int(input())
p = list(int(input()) for i in range(n))
print(sum(p) - (max(p)//2))

#C - Christmas Eve
Difficulty : 243
例1 では 1, 3, 5 本目の木を選んで正解としていますが、1, 3, 5 をそのまま選ぶ、というのは難しいです。
例えば、この木が『10, 11, 12, 14, 15』と、昇順に並んでいると考えると、答えとなる木が 1, 2, 3 本目と連番になり、答えを出しやすくなります。
なので、あらかじめ $h$ をソートしておきます。
そして、for を使い前から順番に $h_{max} - h_{min}$ を計算し、最小の差を求めます。

n,k = map(int,input().split())
h = list(int(input()) for i in range(n))
h.sort()
ans = 10**16
for i in range(n-k+1):
    ans = min(ans,h[i+k-1]-h[i])
print(ans)

#D - Christmas
Difficulty : 1084
この問題の多次元バーガーは以下のようになります。

レベル0 P
レベル1 BPPPB
レベル2 BBPPPBPBPPPBB
レベル3 BBBPPPBPBPPPBBPBBPPPBPBPPPBBB
︙

この問題は最大レベル 50 であり、この時の大きさは例 3 から $10^{15}$ を軽く超え、単純にバーガーを作って数えると実行時間制限に間に合わなくなります。
なので、工夫をしてパティの枚数を求める必要があります。
まず、レベルごとの厚さ $a$ 、レベルごとのパティの総数 $p$ を求めます。
レベル 0 はそれぞれ 1 と最初からわかりますが、レベル 1 以上は計算で求める必要があります。
$a_i$ は『バン、$a_{i-1}$、パティ、$a_{i-1}$、バン』で構成されるので、$a_i = a_{i-1} \times 2 + 3$ になります。
$p_i$ は 上の構成からバンを引く必要があるので、$p_i = p_{i-1} \times 2 + 1$ になります。

a[i] = 2 × a[i-1] + 3 
p[i] = 2 × p[i-1] + 1

そして、レベル N の下から X 層に含まれるパティの層数を $f(N,X)$ とします。
さらに、レベル 0 の場合は簡単に求まることを活用して、「レベル N-1 に対して、どんな整数 Y を指定されても $f(N-1,Y)$ が分かる。」と仮定すると、次のようにレベル N バーガーについても求めることができます。

1. X = 1 のとき 
   N = 1 なら f(N,X) = 0
   N = 0 なら f(N,X) = 1
   レベル 0 を除くと、どのレベルでも一番下はバンになるためパティは 0 枚になります。

2. 1 < X ≦ 1 + a[N-1] のとき f(N,X) = f(N-1,X-1)
   X がレベル N-1 の厚さ + 1 に収まる場合です。
   1 を足す理由は、レベル N-1 からレベル N を構成するときに足した下のバンの分です。
   レベル N-1 の X 層のパティの枚数を求める必要があるので、f(N-1,X-1) を呼び出します。
   1 を引く理由は足したときと同じ理由になります。

3. X = 2 + a[N-1] のとき f(N,X) = p[N-1] + 1
   X がレベル N-1 の厚さに、レベル N を構成するときに足した下のバンと真ん中のパティを含めた厚さと同じ場合です。
   この場合はレベル N-1 のパティの枚数にレベル N の構成時に追加した真ん中のパティ 1 枚を足した枚数になります。

4. 2 + a[N-1] < X ≦ 2 + 2a[N-1] のとき f(N,X) = p[N-1] + 1 + f(N-1,X-2-a[N-1])
   条件 2 と 3 を混合したようなイメージです。
   3 と同じように真ん中のパティまでの枚数を計算で求めます。
   さらに、真ん中から上のパティの枚数を求めたいので、f(N-1,X-2-a[N-1]) を呼び出します。
   X の部分は X から 3 の長さを引いているだけです。 

5. X = 3 + 2a[N-1] のとき f(N,X) = 2p[N-1] + 1
   X がそのまま現在のレベル N の厚さの場合です。
   この場合は最初に計算していたように、2 × p[N-1] + 1 で求まります。

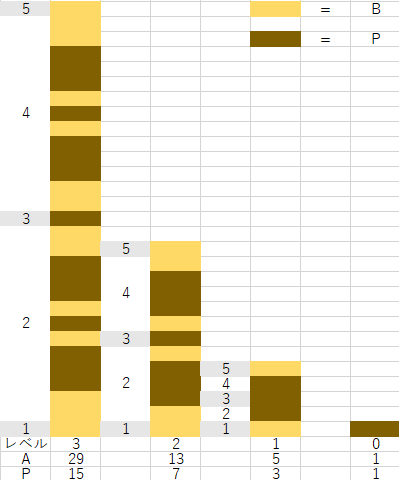
ここまでの流れを図に表すとこうなります。
黄色の B がバン、茶色の P がパティとして見てください。

この条件を再帰関数として書き、$f(N,X)$ を呼び出せば答えが求まります。

n,x = map(int,input().split())
a,p = [1],[1]
for i in range(n):
    a.append(a[i] * 2 + 3)
    p.append(p[i] * 2 + 1)

def pate(n,x):
    if x == 1:
        if n == 0:
            return 1
        else:
            return 0
    elif x <= 1 + a[n-1]:
        return pate(n-1,x-1)
    elif x == 2 + a[n-1]:
        return p[n-1] + 1
    elif x <= 2 + 2 * a[n-1]:
        return p[n-1] + 1 + pate(n-1,x-2-a[n-1])
    else:
        return 2 * p[n-1] + 1

print(pate(n,x))