yukicoder No.1928 Make a Binary Tree

データ構造をマージする一般的なテクをひらめけなかったのでまとめておく
使用言語はPython

問題

事前知識

二分木

どの親も、子を3つ以上持たない木のこと
この問題では、ある親に対して子を2つまで繋げられるという解釈でよい

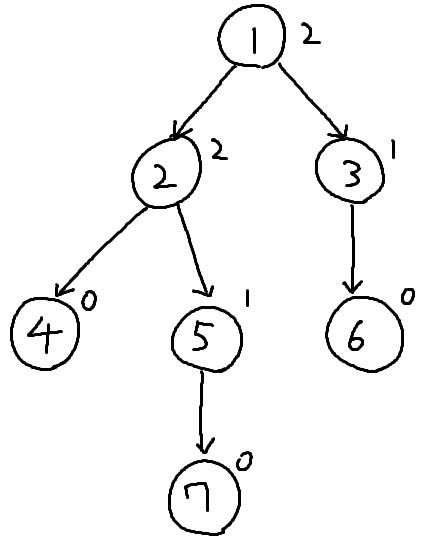
解説

まず、各頂点で「頂点 $i$ を親としたときに残せる最大の頂点数」を求めることを考える、最終的な答えは頂点 1 の値になる

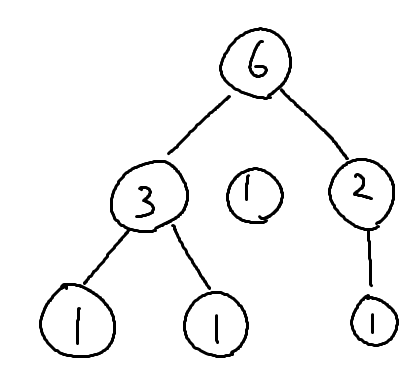
頂点 $i$ の値を求めるには、その子の値を全て求めてからでないと残す頂点を決めることができないので、DFS(深さ優先探索)で順に求めることになる

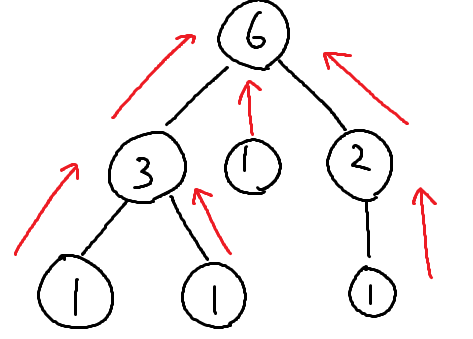
親が選べる頂点のうち、最大と 2 番目に大きい値の子を選ばないといけないのだが、どこかのタイミングで切り捨てたものが 2 番目に大きい場合もあるため、選ばなかった頂点もまとめる必要がある

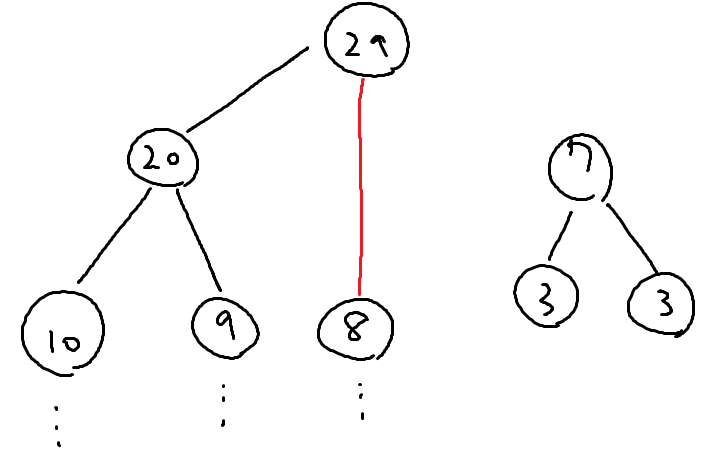
そこで、次のような操作を行う
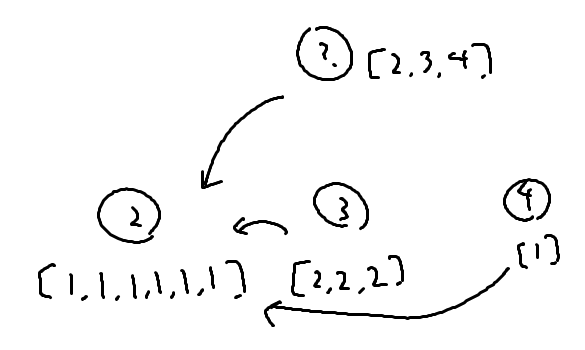
まず、子の値を全て求め、それを親のリストに格納する

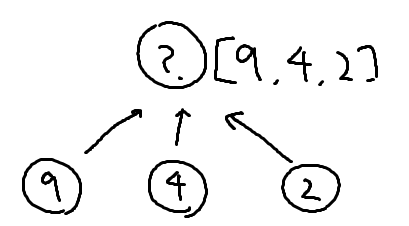
もし子のリストに値が残っている場合は、それを全て親のリストに移す

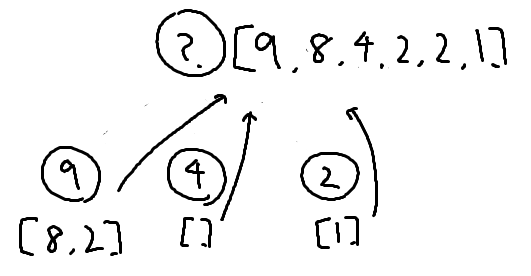
リストから最大の値を 2 つまで取り出し、取り出した分と自身の頂点分を加えた値と頂点の値とする

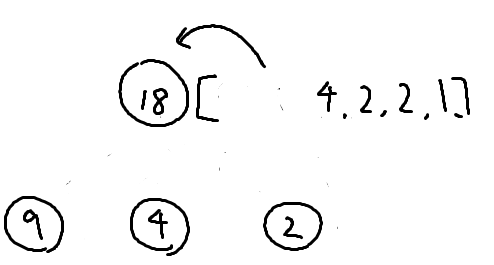
この操作を行うことによって切り捨てた分も候補に入れることができ、問題なく値を求めることができる
Pythonではリストの部分は優先度付きキューを用いることで高速に最大 2 つの値を取り出せる

ただし、子のリストが多く残っていると移すときに時間がかかるため、もう一工夫必要である

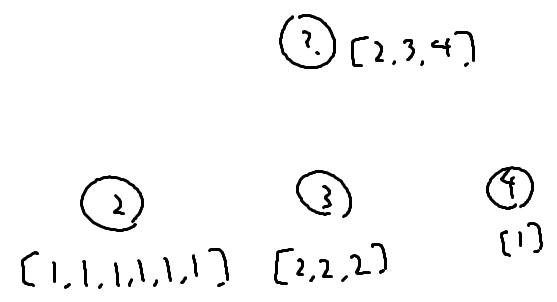
最終的に子の要素が全て親に集約されるため、子のリストに移してからそれを親のリストとして扱っても問題ない
そのため、子の値を親のリストに格納していき、格納が終わった時点でのリストの長さが最大の頂点に値を集約し、それを親のリストとして使えば移す回数を減らせる

提出コード

from sys import setrecursionlimit
setrecursionlimit(10**6)

from heapq import heappop,heappush

def dfs(pos, pre):
    global G, Vec
    for nxt in G[pos]:
        if nxt == pre:
            continue
        P = dfs(nxt, pos)
        heappush(Vec[pos], -P)
    M = len(Vec[pos])
    idx = pos
    for nxt in G[pos]:
        if nxt == pre:
            continue
        if len(Vec[nxt]) > M:
            M = len(Vec[nxt])
            idx = nxt
    if idx != pos:
        while Vec[pos]:
            heappush(Vec[idx], heappop(Vec[pos]))
    for nxt in G[pos]:
        if nxt == pre:
            continue
        if nxt == idx:
            continue
        while Vec[nxt]:
            heappush(Vec[idx], heappop(Vec[nxt]))
    Vec[pos] = Vec[idx]
    ret = 1
    if len(Vec[pos]) <= 2:
        while Vec[pos]:
            ret += -heappop(Vec[pos])
    else:
        for _ in range(2):
            ret += -heappop(Vec[pos])
    return ret

N = int(input())
G = [[] for _ in range(N)]
for _ in range(N-1):
    x,y = map(int,input().split())
    x -= 1
    y -= 1
    G[x].append(y)
    G[y].append(x)
Vec = [[] for _ in range(N)]
print(dfs(0, -1))

感想

本番中は DFS で深い順に求めるのは分かっていたが、マージテクを知らなかったため、切り捨てた頂点の扱いが上手くできず正解できなかった
解説を見た時めちゃくちゃ感動した