電波干渉計の観測を雑にPythonで表現してみた

電波干渉計は開口合成という技術を使って天体の電波画像を取得する望遠鏡です。現時点で世界を代表する電波干渉計は、国立天文台を含む国際協力のもとで南米チリで建設・運用されているALMA望遠鏡でしょう。ホームページにはさまざまな天体の画像が紹介されています。でも電波干渉計の画像復元プロセスはちょっとクセがあり、そこに紹介されている画像を作るまでには複雑なプロセスを踏む必要があります。正確さを犠牲にして極限まで単純化したPythonコードで、電波干渉計で画像を取得するプロセスの最も基本的な部分を表現してみました。

なお、ここでは添付の画像を生成するコードは示していません。添付画像の生成を含むPythonコードの全体像はGistにまとめました。

環境

以下のコードは下に示す環境で実行しました。

• Python 3.10.8
• numpy 1.23.4
• scipy 1.9.3
• opencv-python 4.6.0

また、添付の画像はmatplotlibで生成しました。

元画像の取得

以下のコードではALMA望遠鏡のWEBサイトから画像をお借りしました。

124億光年先のモンスター銀河COSMOS-AzTEC-1（想像図）

元画像の著作権は国立天文台にあります。

これをダウンロードして、正方形に切り抜きます。以降のコードではこれを単色画像に変換して擬似観測を行います。

import os
import urllib.request as request

import cv2

url = 'https://alma-telescope.jp/assets/uploads/2018/08/AzTEC-1_impressions-1.jpg'
imagename = os.path.basename(url)

# 画像のダウンロード
if not os.path.exists(imagename):
    req = request.urlopen(url)
    with open(imagename, 'wb') as fd:
        fd.write(req.read())

# メモリにロード
image = cv2.imread(imagename)

# 正方形に切り出して保存
square_image = image[:, 750:-750, :]
cv2.imwrite('input_image.png', square_image)

天体の直接撮像観測

まず比較のために、天体観測として思い浮かべるであろう、直接撮像観測をPythonで表現してみたいと思います。最近のスマホには高性能なカメラがついていますので、スマホで月を撮影したりなんていうことも簡単にできてしまいます。2022年11月の皆既月食で赤い月を撮影された方も多いのではないでしょうか。これも立派な「観測」ですが、数学的には天体の真の電波画像に点像分布関数（Point Spread Function = PSF）を畳み込んだことに対応します。

import cv2
import numpy as np
import scipy.signal as signal

imagename = 'input_image.png'

# 白黒画像にする
grey_image = cv2.cvtColor(cv2.imread(imagename), cv2.COLOR_RGB2GRAY)

# PSF (2次元のGaussian)
n_psf = 32
sigma = 8
gauss = signal.windows.gaussian(n_psf, std=sigma)
psf = np.multiply(gauss.reshape((1, n_psf)), gauss.reshape((n_psf, 1)))

# 観測画像 = PSF * 真の画像
obs_image = signal.convolve2d(grey_image, psf, mode='same')

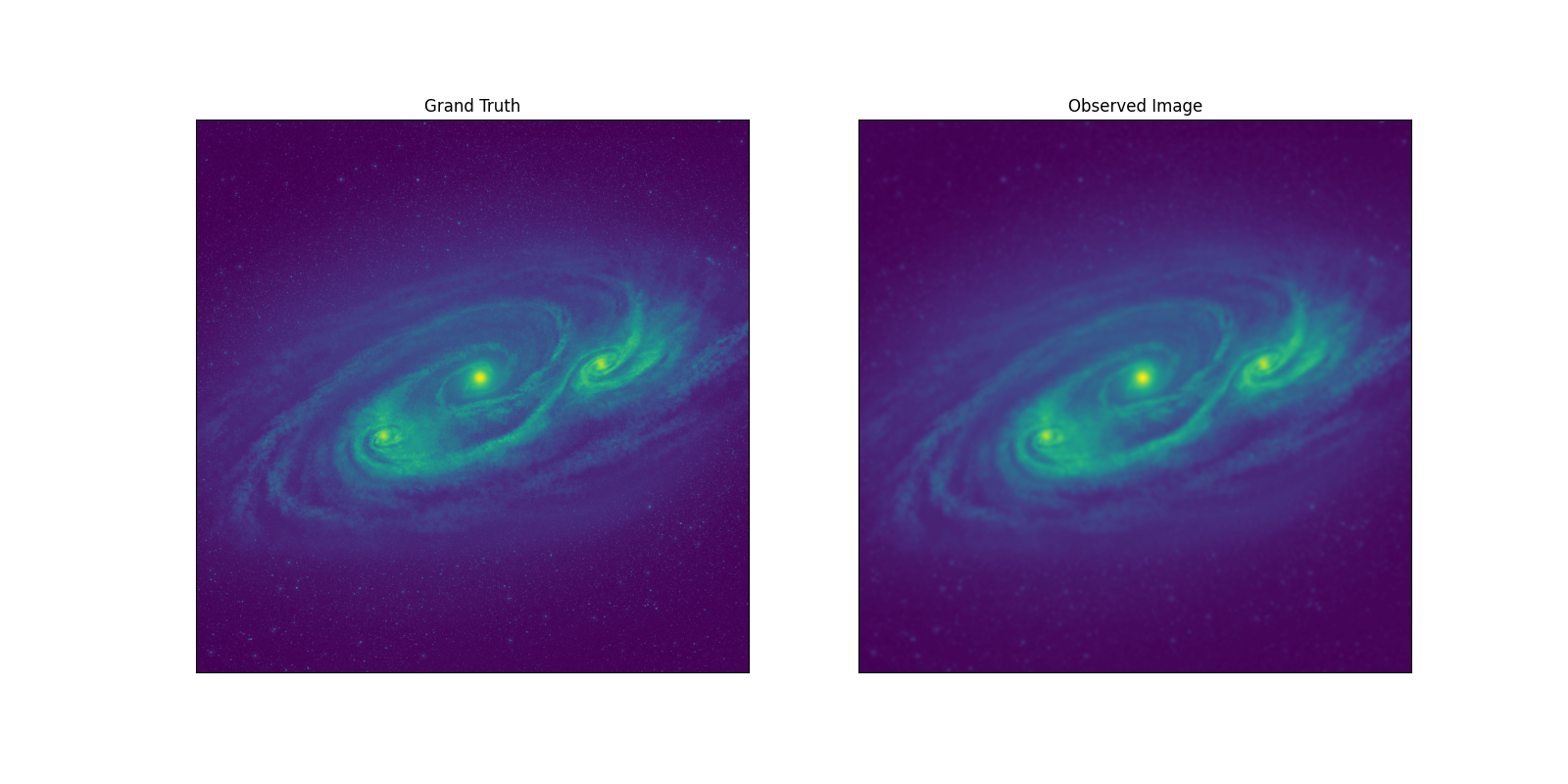
真の画像（左）に比べると、観測画像（右）は若干ぼやけたような見た目になっているかと思います。これはPSFの効果です。カメラの解像度が有限であることを表しています。

電波干渉計の観測

天体の直接撮像観測は真の画像にPSFを畳み込むことで表現しました。電波干渉計はどうでしょうか。

電波干渉計は「空間周波数フィルタ」

電波干渉計は直接電波画像を撮影することはできません。その代わり、２つのアンテナのペアを使って、電波画像のフーリエ成分を測定します。

import cv2
import numpy as np
import scipy.signal as signal

imagename = 'input_image.png'

# 白黒画像にする
grey_image = cv2.cvtColor(cv2.imread(imagename), cv2.COLOR_RGB2GRAY)

# 電波干渉計は画像のフーリエ成分を測定する
vis = np.fft.fft2(grey_image, norm='ortho')

# フーリエ成分（複素数）の振幅を求める
vis_shift = np.fft.fftshift(vis)
vis_amp = np.abs(vis_shift)

真の画像（左）をフーリエ変換すると、右のようなフーリエ空間が得られます（フーリエ成分は振幅のログスケールをプロットしています）。電波干渉計は、フーリエ空間上の各ピクセルを地道にサンプリングする装置です。正確さを欠いていることを承知でおおざっぱにいうと、アンテナペア一組による一回の測定が右図のピクセルひとつに対応すると思ってください。言い換えると、電波干渉計を構成するアンテナの各ペアは、観測する電波の周波数、天体の位置関係、アンテナ間の距離で決まる天体画像の特定の空間周波数に感度を持った「空間周波数フィルタ」になっています。したがって、さまざまな位置関係、さまざまなアンテナ間隔でフーリエ空間をサンプリングしていき、全ての空間周波数成分をサンプリングすることができれば、逆フーリエ変換により真の画像を復元することができます。

電波干渉計の現実

しかし現実はそう甘くありません。フーリエ空間をすべて埋めるためには、アンテナ間隔を0から無限大まで取らなければなりません。もちろんそんなことは無理です。観測サイトの地理的条件をはじめとしたさまざまな制約により、現実的に取りうるアンテナ間隔には上限が出てしまいます。フーリエ空間の言葉であらわすと、取得できるフーリエ成分の、特に高空間周波数成分には必ず上限が存在します（ついでに言うと、低空間周波数側にも限界があります）。また、理論的には観測可能な範囲も１００％サンプリングすることは不可能です。この状況を模式的にコーディングしてみます。

# 高い空間周波数はサンプリングできないことを表すマスク配列
cx = vis_amp.shape[0] // 2
cy = vis_amp.shape[1] // 2
rlimit = cx * 1 / 2
mask = np.zeros_like(vis_amp)
for i in range(vis_amp.shape[0]):
    for j in range(vis_amp.shape[1]):
        radius = np.sqrt(np.square([cx - i, cy - j]).sum())
        if radius < rlimit:
            mask[i, j] = 1

# 分解能が制限された電波画像
vis_observed = vis * np.fft.ifftshift(mask)
dirty_image_10 = np.fft.ifft2(vis_observed, norm='ortho').real

# 観測可能な範囲のサンプリングも不完全であることを表すマスク配列
idx = np.where(mask == 1)
nvalid = len(idx[0])
coverage = 0.3
frac = 1
mask3 = mask.copy()
while frac > coverage:
    unobserved = np.random.randint(0, len(idx[0]), size=int(len(idx[0]) * (1 - coverage)))
    mask3[idx[0][unobserved], idx[1][unobserved]] = 0
    idx = np.where(mask3 == 1)
    frac = len(idx[0]) / nvalid


# 実際に観測される電波画像（ダーティイメージ）
vis_observed = vis * np.fft.ifftshift(mask3)
dirty_image_3 = np.fft.ifft2(vis_observed, norm='ortho').real

上段はフーリエ空間を全てサンプリングした場合で、この場合は真の画像を復元できます。

中段は観測可能な空間周波数成分が制限されている状況で、これは直接撮像観測において分解能が有限であることに対応しています。実際観測されなかった領域のフーリエ成分を全てゼロとして（ゼロパディング）逆フーリエ変換すると、真の画像をややぼかしたような画像が得られています。

そして下段が電波干渉計の観測にもっとも近い状況です。ここでは観測可能な空間周波数成分のうち、3割しか観測できなかった場合を示しています。本来はアンテナの配置や観測する天体の方向によって観測可能なフーリエ成分に特徴的なパターンが現れるのですが、ここでは簡単のためランダムにデータを欠損させました。中段と同様にゼロパディングして逆フーリエ変換すると、全体的にぼやけた画像に雲のような偽の構造が現れています。この偽の構造はフーリエ空間での観測が不完全なことと、観測できなかったフーリエ成分をゼロパディングしたことに起因するもので、偽の構造に汚されたように見えることからこの状態をダーティイメージまたはダーティマップと呼びます（日本語に無理やり訳すと「汚れた画像」）。

ダーティイメージが電波干渉計の「生画像」ですが、このような画像は科学的には使い物になりません。ですがダーティイメージの「汚れのパターンや程度」は、フーリエ空間で観測されたピクセルの分布から推定することができます。伝統的には、性質がわかっている「汚れ」をダーティイメージからきれいに拭き取ることにより、確からしい復元画像を生成しています。この伝統的な画像復元プロセスはCLEAN（クリーン）法と呼ばれています。CLEAN法なしには電波干渉計の最終結果である電波画像は得られないため、CLEAN法も電波干渉計を構成するシステムの重要な一部であると言えると思います。まとめますと、電波干渉計とは以下のような観測装置です。

• 電波干渉計は天体画像のフーリエ成分を観測する「空間周波数フィルタ」
• なるべく多くのフーリエ成分を観測することで、フーリエ成分から天体画像を復元する
• ただしデータが欠損するので画像の復元には工夫が必要（具体的な手法は、続編記事電波干渉計の画像復元を雑にPythonで表現してみたで紹介しています）