はじめに(Introduction)
YouTubeを見ていたら、「パロンドのパラドックス」という直感に反した結果(パラドックス)について解説していました。
前回に続いて、内容が非常に面白かったので、実際にプログラムでシミュレーションを行ってみます。
ゲーム(Game)
3つのゲームA、B、Cがあります。
ゲームA、Bは不利なゲームですが、ゲームAとゲームBを組み合わせたゲームCは得となるゲームになるという事です。
ゲームA(Game A)
ゲームの条件は以下のとおりです。
- 48%の確率で+1ドル
- 52%の確率で-1ドル
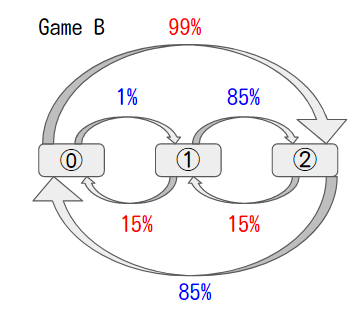
ゲームB(Game B)
ゲームの条件は以下のとおりです。
- 所持金が3の倍数の場合
- 1%の確率で+1ドル
- 99%の確率で-1ドル
- 所持金がそれ以外の場合
- 85%の確率で+1ドル
- 15%の確率で-1ドル
ゲームC(Game C)
ゲームの条件は以下のとおりです。
- 50%の確率でゲームA
- 50%の確率でゲームB
期待値(Expected value)
ゲームAの期待値(Expected value of Game A)
この期待値は簡単に求められます。
$(+1)\times \frac{48}{100} + (-1)\times \frac{52}{100} = -0.04$
ゲームBの期待値(Expected value of Game B)
所持金が3の倍数かどうかによって状況がかわる為、状態遷移図を使うようです。
⓪①②は、所持金を3で割った余りを示しています。
この3か所それぞれにいる確率を計算します。
⓪にいる確率を $x$、①いる確率を $y$、②にいる確率を $z$ とします。
以下の連立方程式を解く事で $x$、$y$、$z$ の値が求められます。
$x=\frac{15}{100}y+\frac{85}{100}z$
$y=\frac{1}{100}x+\frac{15}{100}z$
$z=\frac{99}{100}x+\frac{85}{100}y$
$x+y+z=1$
期待値 $e$ は、$x$、$y$、$z$ の位置から、$+1$、$-1$の確率を計算すればいいわけです。
$e = (+1)x\frac{1}{100} + (-1)x\frac{99}{100} + (+1)y\frac{85}{100} + (-1)y\frac{15}{100} + (+1)z\frac{85}{100} + (-1)z\frac{15}{100} $
Pythonで解を求めてみます。
import sympy as sp
sp.var('x, y, z')
eq1=sp.Eq(x, 0.15*y+0.85*z)
eq2=sp.Eq(y, 0.01*x+0.15*z)
eq3=sp.Eq(z, 0.99*x+0.85*y)
eq4=sp.Eq(x+y+z, 1)
ans = sp.solve([eq1, eq2, eq3, eq4], [x, y, z])
print(ans)
e = (+1)*ans[x]*0.01 + (-1)*ans[x]*0.99 + (+1)*ans[y]*0.85 + (-1)*ans[y]*0.15 + (+1)*ans[z]*0.85 + (-1)*ans[z]*0.15
print(e)
{x: 0.429908844542991, y: 0.0780980537078098, z: 0.491993101749199}
-0.0222468588322247
期待値は約$-0.022$となります。
ゲームCの期待値(Expected value of Game C)
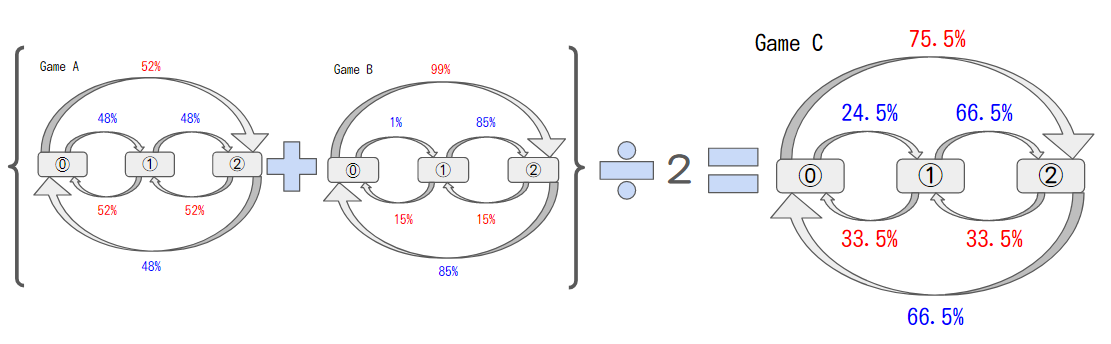
状態遷移図をゲームAでも作成します。
この状態遷移図をゲームAとゲームBを足して2で割れば良いという事になります。
先ほどと同様に、⓪①②は、所持金を3で割った余りを示しています。
この3か所それぞれにいる確率を計算します。
⓪にいる確率を $x$、①いる確率を $y$、②にいる確率を $z$ とします。
以下の連立方程式を解く事で $x$、$y$、$z$ の値が求められます。
$x=\frac{33.5}{100}y+\frac{66.5}{100}z$
$y=\frac{24.5}{100}x+\frac{33.5}{100}z$
$z=\frac{75.5}{100}x+\frac{66.5}{100}y$
$x+y+z=1$
期待値 $e$ は、$x$、$y$、$z$ の位置から、$+1$、$-1$の確率を計算すればいいわけです。
$e = (+1)x\frac{24.5}{100} + (-1)x\frac{75.5}{100} + (+1)y\frac{66.5}{100} + (-1)y\frac{33.5}{100} + (+1)z\frac{66.5}{100} + (-1)z\frac{33.5}{100} $
Pythonで解を求めてみます。
import sympy as sp
sp.var('x, y, z')
eq1=sp.Eq(x, 0.335*y+0.665*z)
eq2=sp.Eq(y, 0.245*x+0.335*z)
eq3=sp.Eq(z, 0.755*x+0.665*y)
eq4=sp.Eq(x+y+z, 1)
ans = sp.solve([eq1, eq2, eq3, eq4], [x, y, z])
print(ans)
e = (+1)*ans[x]*0.245 + (-1)*ans[x]*0.755 + (+1)*ans[y]*0.665 + (-1)*ans[y]*0.335 + (+1)*ans[z]*0.665 + (-1)*ans[z]*0.335
print(e)
{x: 0.354399644335009, y: 0.227044218733969, z: 0.418556136931022}
0.0323042987585924
期待値は約$0.032$となります。
期待値が負と負のゲームを組み合わせると期待値が正になります。
※注意※動画内の値とは異なります。(計算の方法が間違っているか、前提が間違っている可能性があります。)
シミュレーション(Simulation)
今回グラフも見たいので、Pythonを使います。
持ち金が$10,000$からスタートして、$10,000$回ゲームを繰り返してみます。
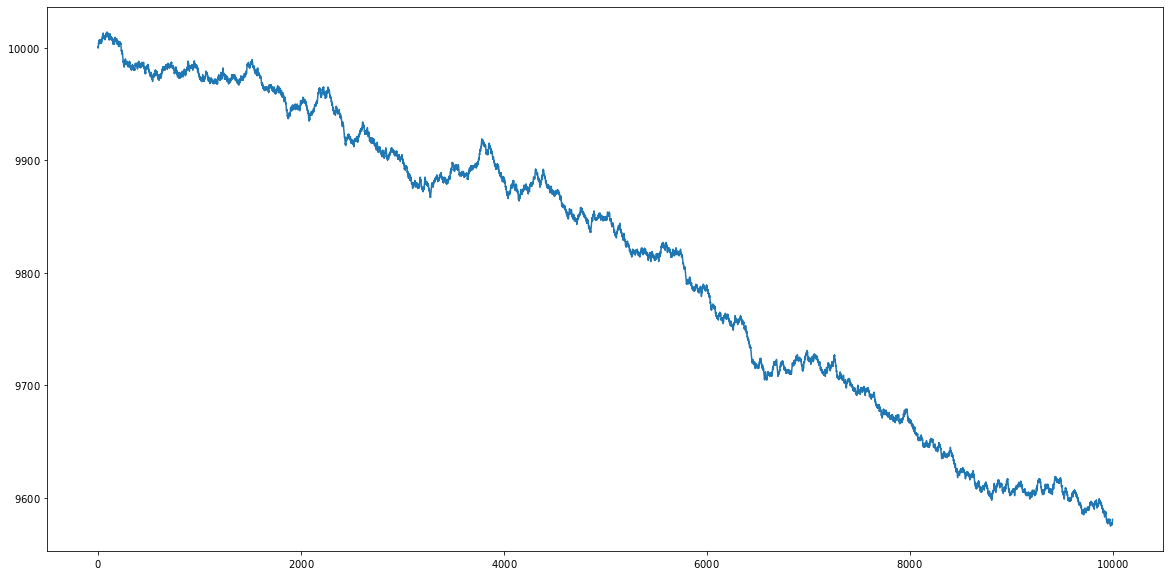
ゲームAのシミュレーション(Simulation of Game A)
期待値的には、$10000+(-0.04)*10000=9600$ となると予想されます。
結果は、$10,000 \rightarrow 9,582$ なのでほぼ期待値と同じであるといえます。
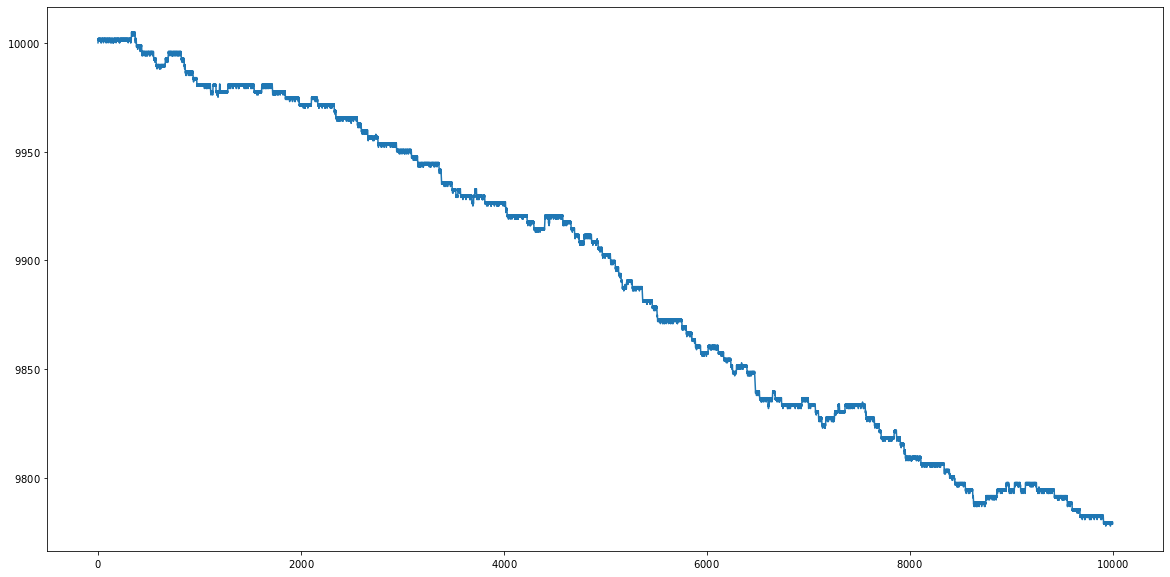
ゲームBのシミュレーション(Simulation of Game B)
期待値的には、$10000+(-0.022)*10000=9780$ となると予想されます。
結果は、$10,000 \rightarrow 9,780$ なので期待値と同じであるといえます。
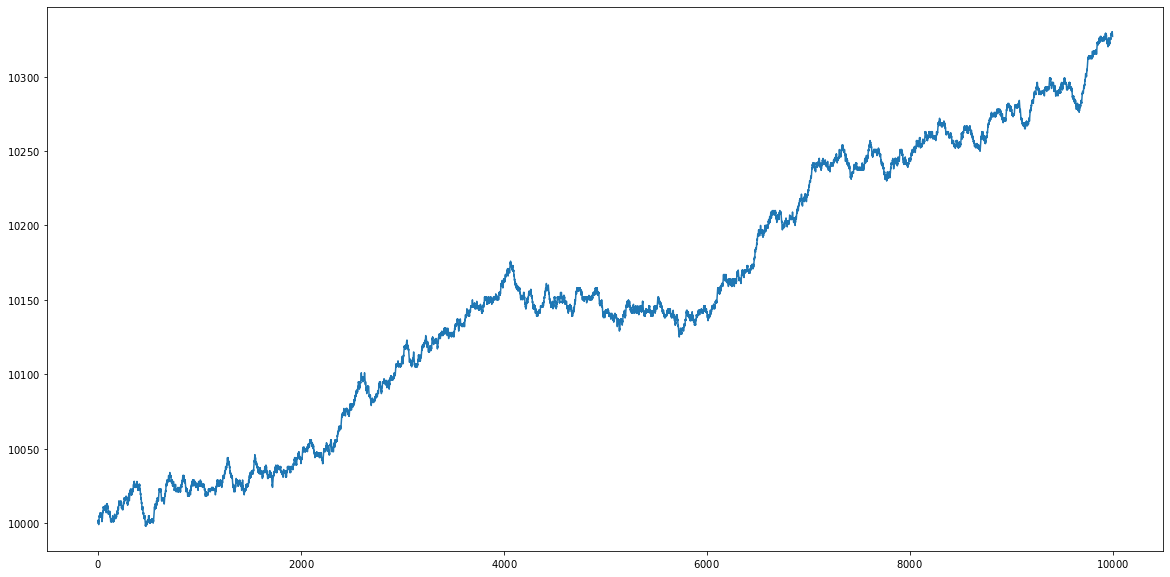
ゲームCのシミュレーション(Simulation of Game C)
期待値的には、$10000+(0.032)*10000=10320$ となると予想されます。
結果は、$10,000 \rightarrow 10,326$ なので期待値と同じであるといえます。
コード
以下のリンク先に今回使用したPythonのコードがあります。
まとめ(Conclusion)
このケースは良い値を選んでいるとの事なので、すべての事象で適用されるわけでは無いようです。
不利なゲームと不利なゲームの
上手いミックス方法があれば
有利なゲームにできる
また、この「パロンドのパラドックス」は比較的最近提唱されたものらしく、いろんな事が分かってきたそうです。
(生物で)
単独では不利なものが合わさって
プラスになっていることがある
そして、金融などさまざまな分野でも研究されているそうです。
個人的な見解ですが、ゲームBの条件に自身の所持金をパラメータに持っている事が重要な気がします。
しかし、不利なゲームを組み合わせると得をするといった直感的な感覚から反する事を行っているのは事実であります。
動画内でもありましたが、得なゲームを組み合わせると不利になるような状態も作れそうです。
ちゃんと理解していないと、今後得すると思っていながら、不利なゲームをしている可能性もありそうです。
参考(References)