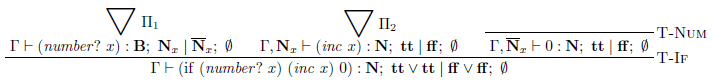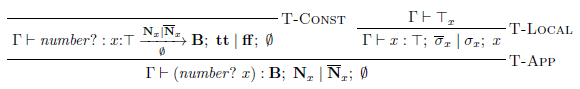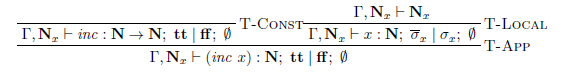この記事は Clojure Advent Calendar 2016 の14日目の記事です。
今年開催されたシンポジウム ESOP 2016 で、Typed Clojureの型システムについて述べた論文 "Practical Optional Types for Clojure" [1] が発表されました。本記事では、この論文で定義されている Typed Clojure の型システムを簡単に紹介したいと思います。
Typed Clojure 入門
Typed Clojure は、動的型付け言語であるClojureに静的型付けの型システムを導入したものです。"オプショナル型システム" を標榜していることから分かるように、静的型検査をプログラムのどの部分に適用するかはプログラマが選択することができます。そのため、プログラマは動的型付け言語の柔軟性と静的型検査によりもたらされる安全性との両方を享受することができます。つまり、いいとこどりができるって訳です。
次のコードは [2, Example 1] で紹介されている Typed Clojure の簡単なプログラム例です。同じプログラムが こちらからダウンロードでき、READMEに書いてある要領で実際にこのプログラムの型検査を行うことができます。
; [2, Example 1] より
(ns demo.eg1
(:refer-clojure :exclude [fn])
(:require [clojure.core.typed :refer [fn U Num]]))
(fn [x :- (U nil Num)]
(if (number? x) (inc x) 0))
最初の3行 (ns ...) はとりあえず「おまじない」と思ってもらうとして、最後の2行に型アノテーションつきの関数式が書かれています。このプログラムに対して、Typed Clojure は型の整合性がとれていることを静的に検査することができます。
x :- (U nil Num) と書くことで、x の値が nil か整数のどちらかの値であることを表すことができます。ここで、型 (U nil Num) は nil と Num の(タグなし)合併型 (untagged union type) と呼ばれるものです。合併型は特に目新しい概念ではなく、C/C++の共用体と同じ概念です。
一方で、次のコードを見てみましょう。
(ns demo.eg1
(:refer-clojure :exclude [fn])
(:require [clojure.core.typed :refer [fn U Num]]))
(fn [x :- (U nil Num)]
(if (number? x) 0 (inc x))) ; 型エラー!
このコードは型検査を通りません! なぜなら、inc は Num 型の値を引数に期待する関数であるのに、if 式の else 節に現れている x は nil だからです。
このように制御フローを考慮した静的型付けは、Typed Clojure の型システムの特徴の一つです。こうした、制御フローの条件式をもとに型付けを行うアプローチは、occurrence typing (出現型付け?)として知られます。元々 Typed Racket で導入された技術であり、Typed Clojure はそれをそのまま輸入しています。
型
それではここから本題です。この記事では、[1] の代わりにそのドラフト版 [2] の定式化に沿って説明をしていきたいと思います。([2] の方が読みやすかったので。)[1] のプレプリントは こちらから、ドラフト版 [2] は こちらから、それぞれPDFで入手できます。
Typed Clojure(の形式的モデル $\lambda_\mathit{TC}$)の型システムで扱われる型には、主に次のようなものがあります。
| 型 | 説明 |
|---|---|
| $\mathbf{N}$ | 整数型 |
| $\mathbf{B}$ | ブール型 |
| $\mathbf{false}$ | 値に false のみを持つ型 |
| $\mathbf{nil}$ | 値に nil のみを持つ型 |
| $\top$ | トップ型(すべての型を部分型とする型。Objectみたいな。) |
| $(\bigcup\ \tau_1 \dots \tau_n)$ | 型 $\tau_1, \dots, \tau_n$ の合併型 |
| $x{:}\tau_1 \xrightarrow[o]{\psi_1 \mid \psi_2} \tau_2$ | 引数型 $\tau_1$、返却型 $\tau_2$ の関数型(下記参照。) |
(数式の表示が崩れる場合は、数式上で右クリックして [Math Settings] -> [Math Renderer] -> [SVG] を選択してください。)
関数型が仰々しい形をしていますが、難しくはありません。$\psi_1$ と $\psi_2$ は下記の意味を持ちます。(矢印の下の $o$ については説明を省略します。)
- $\psi_1$ は、関数適用の結果が真に評価される場合に成り立つ命題を表す。
- $\psi_2$ は、関数適用の結果が偽に評価される場合に成り立つ命題を表す。
例えば、関数 $\mathit{number?}$ の型は次のようになります。
x{:}\top \xrightarrow[\emptyset]{\mathbf{N}_x \mid \overline{\mathbf{N}}_x} \mathbf{B}
ここで、$\mathbf{N}_x$ は変数 $x$ の型が $\mathbf{N}$ であること、$\overline{\mathbf{N}}_x$ は変数 $x$ の型が $\mathbf{N}$ でないことを表します。つまり、この型を持つ関数において、関数適用の結果が真に評価されるならば引数の型は整数型であることが保証され、偽に評価されるならば引数の型は整数型でないことが保証されます。
関数 $\mathit{inc}$ の型は次のようになります。
x{:}\mathbf{N} \xrightarrow[\emptyset]{\mathbf{tt} \mid \mathbf{ff}} \mathbf{N}
関数 $\mathit{inc}$ の関数適用の結果は整数であり、常に真に評価されるため、$\psi_1$ は恒真を表す $\mathbf{tt}$ に、$\psi_2$ は恒偽を表す $\mathbf{ff}$ になっています。
型判定式
素朴な型システムは、例えば次のような 3 項組(型判定式 (type judgement) と呼ばれる)を導出する推論規則群により定義されるのが普通です。
\{ x : \mathbf{N} \} \vdash (\mathit{inc}\ x) : \mathbf{N}
この型判定式は「変数 $x$ の型が $\mathbf{N}$ ならば、式 $(\mathit{inc}\ x)$ の型は $\mathbf{N}$」と読むことができます。これと同等のものが、Typed Clojure では次のような 6 項組になります!
\mathbf{N}_x \vdash (\mathit{inc}\ x) : \mathbf{N};\ \mathbf{tt} \mid \mathbf{ff};\ \emptyset
一般に、Typed Clojure の型システムにおける型判定式は次の形をとります。
\Gamma \vdash e : \tau;\ \psi_+ \mid \psi_-;\ o
これは「$\Gamma$ が成り立つならば、式 $e$ の型は $\tau$」であることを表し、さらに $\psi_+$, $\psi_-$, $o$ は次のような意味を持ちます。
- $\psi_+$ は式 $e$ が真に評価される場合に成り立つ命題を表す。
- $\psi_-$ は式 $e$ が偽に評価される場合に成り立つ命題を表す。
- $o$ は式 $e$ の値に一致するオブジェクトを表す(もしあれば)。
先の例を見ると、整数型の式 $(\mathit{inc}\ x)$ は必ず真に評価されるため、$\psi_+$ は恒真を表す $\mathbf{tt}$ に、$\psi_-$ は恒偽を表す $\mathbf{ff}$ になっています。オブジェクト $o$ は式の値と一致するものが存在すれば書かれますが、この例ではその場合に当たらないため空となっています。
型付け規則
型付け規則は下記のようになっています([2] より抜粋)。
この型付け規則で、次のプログラムの型付けを実際に行ってみましょう。
(fn [x :- (U nil Num)]
(if (number? x) (inc x) 0))
型付け規則に従って導出木を構成すると、次の図のようになります。この導出木は結構頑張って自分で作りました。
ただし、$\Gamma = (\bigcup\ \mathbf{nil}\ \mathbf{N})_x$、$\sigma = (\bigcup\ \mathbf{nil}\ \mathbf{false})$ と置いています。式 $(\mathit{number?}\ x)$ と $(\mathit{inc}\ x)$ に対する導出は別の図に分けました。
式 $(\mathit{number?}\ x)$ に対する導出 $\Pi_1$ は次の通りです。
式 $(\mathit{inc}\ x)$ に対する導出 $\Pi_2$ は次の通りです。
よく見ると $\Gamma \vdash \top_x$ と $\Gamma, \mathbf{N}_x \vdash \mathbf{N}_x$ の導出が示されていませんが、これらは型付け規則とは別の推論規則から導出されます。詳しくは [2] の他に [3] などを参照してください。
まとめ
Typed Clojure の形式的な型システムの定義について駆け足で説明してきました。あまり網羅的な説明はできなかったので、詳細は [1] および [2] を参照してください。また、 occurrence typing まわりの理解には [3] と [4] が読みやすく役立つと思います。
参考文献
- A. Bonnaire-Sergeant, R. Davies, and S. Tobin-Hochstadt. Practical Optional Types for Clojure. In Proc. ESOP 2016, volume 9632 of LNCS, pp. 68-94, Springer, 2016.
- A. Bonnaire-Sergeant, R. Davies, and S. Tobin-Hochstadt. Practical Optional Types for Clojure. Draft version on Feb. 28, 2015. Available at https://github.com/typedclojure/examples.
- S. Tobin-Hochstadt and Matthias Felleisen. Logical Types for Untyped Languages. In Proc. ICFP 2010, pp. 117-128, ACM, 2010.
- A. M. Kent, D. Kempe, and S. Tobin-Hochstadt. Occurrence Typing Modulo Theories. In Proc. PLDI 2016, pp. 296-309, ACM, 2016.