出演者が大勢いる声優イベントに参加すると、当然自分が知らない声優さんもいらっしゃいます。そんな時、出演者の立ち位置や評価を俯瞰できるといいなーと思うことがあったので、簡単に作ってみました。
大体以下のようなテーマで取り組みました。
- ある声優がどのようなクラスタに属していて誰に支持されているのかがわかる
- その声優の流行がわかる
1.は声優とファンのインタラクションを利用して声優をベクトル化できればクラスタリングもできそうなので、レコメンド系の手法をベースにします。2.は時刻に関する情報なので、時系列拡張したレコメンドアルゴリズムを実装してみました。
データ
ユーザーと声優の関係データを用います。声優イベント管理ツールであるEventernoteは、気になる声優をお気に入り登録する機能を提供しています。今回はこのデータを拝借しました。
基本的なレコメンドはユーザーとアイテムの関係のみを入力しますが、今回は流行も可視化したいと考えているので、ユーザーがお気に入り登録した時点のタイムスタンプも入力します。
入力データは、(<user_id>, <actor_id>, <timestamp>)のようなタプルのリストになります。レコメンドのベンチマークであるMovieLensには5段階のratingがついていますが、今回はお気に入り登録したか否かなのでratingに相当するカラムは1のみです。レコードが存在することとrating=1が同値なのでカラムとしては持ちません。
なお、入力するデータはお気に入りが付与された時刻の情報しか持っていないので、このデータでは推し変や他界を検知することはできません。また、声優個人の人気や優劣を定量化するものでもないことを予め述べておきます。
モデル
タスクはレコメンドなのでモデルベース協調フィルタリングの式から出発します。
r_{ui} = \alpha + \beta_u + \beta_i + <\gamma_u, \gamma_i>
$\alpha,\beta_u,\beta_i$はそれぞれglobal、ユーザー、声優のバイアスです。$\gamma_u, \gamma_i$はユーザー、声優の特徴ベクトル、$<a,b>$は$a$と$b$の内積を表します。
声優の流行を、ある時点におけるその声優のバイアスと読み替えて、モデルを以下のように拡張します。
r_{ui}(t) = \alpha + \beta_u + \beta_i(t) + <\gamma_u, \gamma_i>
$\beta_i$を時間依存する項とします。特徴ベクトルは時間に依らず固定です。非常にシンプルです。
なお、後述する推論手法の仕様により$\alpha$と$\beta_u$は推論対象から除外します。よってモデルパラメータは$\beta_i(t), \gamma_u, \gamma_i$の3種類です。
バイアスやインタラクションに時間発展を仮定したモデルは他にも存在しますが、今回は必要最小限の機能を備えているという理由でこのモデルを採用しました。モデルの比較や妥当性の検証はしておりませんのであしからず。
推論
パラメータ更新
Bayesian Personalized Rankingを使います。BPRに関しては解説記事があるので本記事では簡単に済ませます。
BPRはあるユーザーに対して正例のスコア$r_{ui}$が負例のスコア$r_{uj}$よりも大きくなるように学習させる手法です。モデルの評価である尤度関数は正例と負例の差分が入力になります。
l_{uij} = \log \sigma(r_{ui}(t_{ui}) - r_{uj}(t_{ui}))
最適化は勾配法を使います。上記の微分を計算して各パラメータを更新します。
\begin{eqnarray}
r_{uij} &=& r_{ui}(t_{ui}) - r_{uj}(t_{ui}) \\
\beta_i^i(t) &=& \beta_i^i(t) + lr \cdot (\frac{1}{1+\exp(r_{uij})} - \lambda \cdot \beta_i^i(t)) \\
\beta_i^j(t) &=& \beta_i^j(t) + lr \cdot (-\frac{1}{1+\exp(r_{uij})} - \lambda \cdot \beta_i^j(t)) \\
\gamma_u &=& \gamma_u + lr \cdot ( \frac{1}{1+\exp(r_{uij})} \cdot (\gamma_i^i - \gamma_i^j) - \lambda \cdot \gamma_u)\\
\gamma_i^i &=& \gamma_i^i + lr \cdot ( \frac{1}{1+\exp(r_{uij})} \cdot \gamma_u - \lambda \cdot \gamma_i^i) \\
\gamma_i^j &=& \gamma_i^j + lr \cdot (-\frac{1}{1+\exp(r_{uij})} \cdot \gamma_u - \lambda \cdot \gamma_i^j) \\
\end{eqnarray}
区間最適化
バイアス$\beta_i(t)$に関して深掘りします。
本手法では、データを取得した期間を離散化し、さらにそれらをEpochという単位で纏めます(Deep Learningの文脈にけるEpochとは異なるのでご注意ください)。
$\beta_i(t)$の値は$t$が属するEpochに応じて決まるという設定です。$ep(t)$を$t$が属するEpochのインデックスを返す関数とした時、以下のようになります。
beta_i(t) = \beta_{i, k} \ \ \ \ where\ \ ep(t)=k
実装上は、$\beta_{i,k}$はアイテム種類数 x Epoch数のマトリックスで定義できます。
続いてEpochの幅について考えます。各Epochがデータの収集区間を等分する形に定義することもできますが、それだと面白くありません。なのでEpochの幅は可変とし、データに応じて決まる仕掛けにしたいと思います。
Epochの区間推定には動的計画法を使います。
Epoch$k$内における対数尤度$\mathcal{L}_k$は、パラメータを固定すれば$ep(t)$のみに依存します。
\begin{eqnarray}
\mathcal{L}_k & = & \sum_{(u, i, j), ep(t_{ui})=k} l_{uij} \\
& = & \sum_{(u, i, j), ep(t_{ui})=k} (\beta_{i, k} - \beta_{j, k} + <\gamma_u, \gamma_i> - <\gamma_u, \gamma_j>)
\end{eqnarray}
動的計画法は、すべてのEpochにおける対数尤度の総和$\mathcal{L}_k$が最大になるような$ep(t)$を与える手法です。手法の概要についてはこちらの記事が分かりやすかったです。
アルゴリズム
パラメータ更新と動的計画法を交互に実行します。
repeat
1. for each (u, i)
1.1. 負例のサンプリング
1.2. パラメータの更新
2. 動的計画法による区間最適化
until convergence
BPRのイテレーションと区間最適化は同じ回数実行する必要はありません。10イテレーションにつき区間最適化1回くらいで充分だと思います。
また、BPRの学習にはtraining set、動的計画法にはvalidation setを使う必要があることにご注意ください。
実験
データセット
前述の通り、Eventernoteのお気に入り声優データセットを用います。5組以上お気に入り登録をしているユーザー、100個以上お気に入り登録されている声優(アーティストも含む)を分析対象としました。集計期間は2013/01/01から2017/06/30までの4年半です。
モデルの初期化
インタラクションのファクター数は32、Epoch数は6に設定しました。Epochの初期化に関して、4年半を72分割し、各Epochに12ブロックずつ割り当てました。パラメータの初期化は一様乱数を使います。
精度
学習結果をAUCで評価したところ、0.872±0.174を達成しました。パラメータ次第ではまだスコアを伸ばせそうな印象を受けました。Eventernoteデータセットは一般的なレコメンドのベンチマークに比べてかなり簡単なようです。
推定されたEpoch
| Epoch | 区間(bin) | 実際の期間 |
|---|---|---|
| Epoch 0 | 0 - 31 | 2013/01/01 - 2014/12/31 |
| Epoch 1 | 32 - 42 | 2014/12/31 - 2015/09/08 |
| Epoch 2 | 43 - 48 | 2015/09/08 - 2016/01/23 |
| Epoch 3 | 49 - 51 | 2016/01/23 - 2016/03/31 |
| Epoch 4 | 52 - 54 | 2016/03/31 - 2016/06/08 |
| Epoch 5 | 55 - 71 | 2016/06/08 - 2017/06/30 |
区間の幅にばらつきが見られます。Epoch3,4は他のEpochと比べて期間が短いのでEpoch数は5でも良かったかもしれません。
可視化
求めたパラメータを可視化することで声優同士の類似度や勢いの時間発展の様子を観察することができます。
声優の活況度
バイアス項$\beta_i(t)$はインタラクションを除いたスコア、すなわち市場でその声優がどれだけ盛り上がっているか表します。
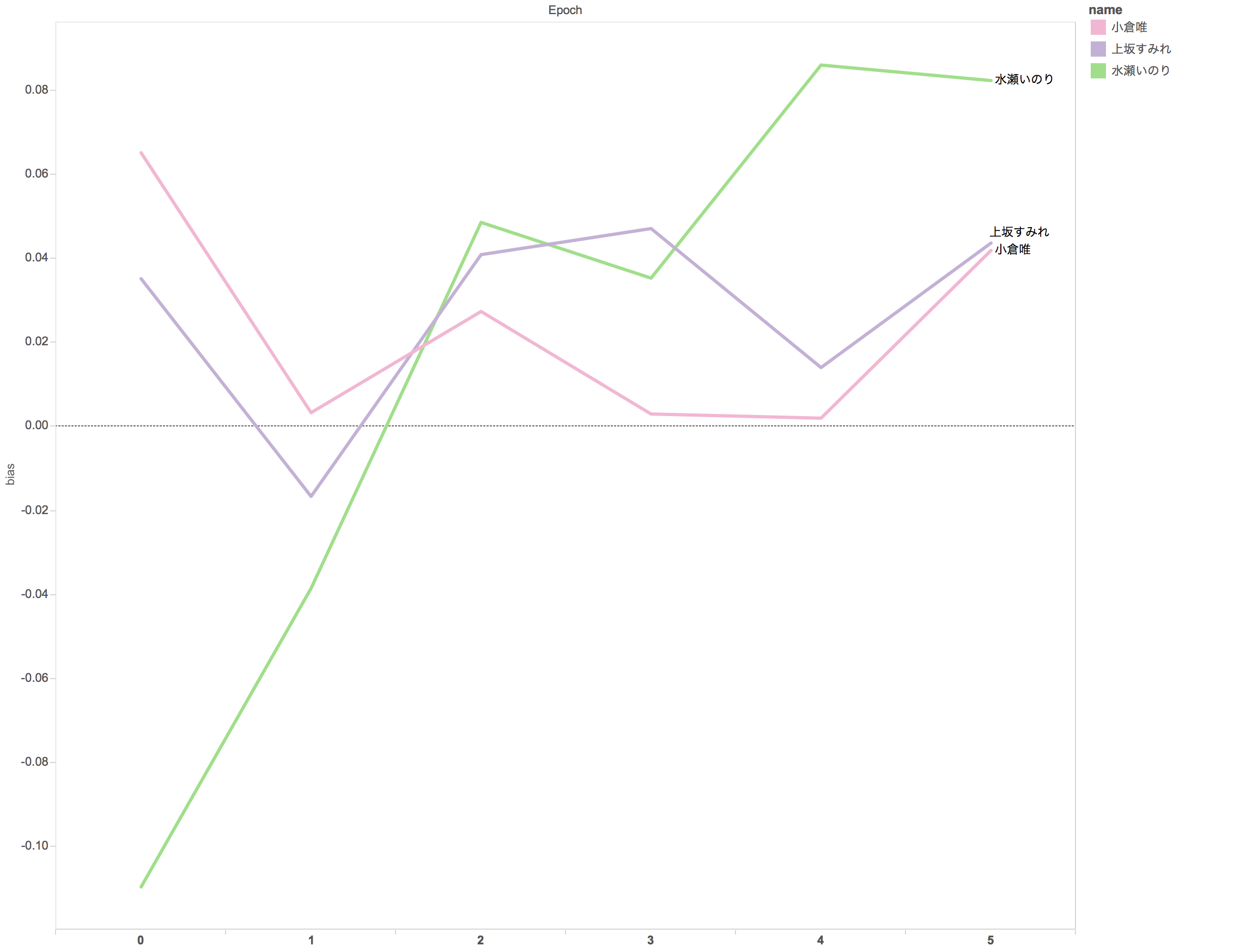
例えば、キングレコードが絶賛売り出し中の3人に関するバイアスの推移は以下のようになります。
水瀬いのりさん強いですね。ごちうさを始め、2014年から2015年にかけて主演の本数が増えているので、Epoch1からEpoch2にかけて急激に立ち上がるのは納得の挙動です。小倉唯さん、上坂すみれさんも高い水準を維持しています。
ところで、本記事を投稿した12月19日は上坂すみれさんのお誕生日です。めでたいです。
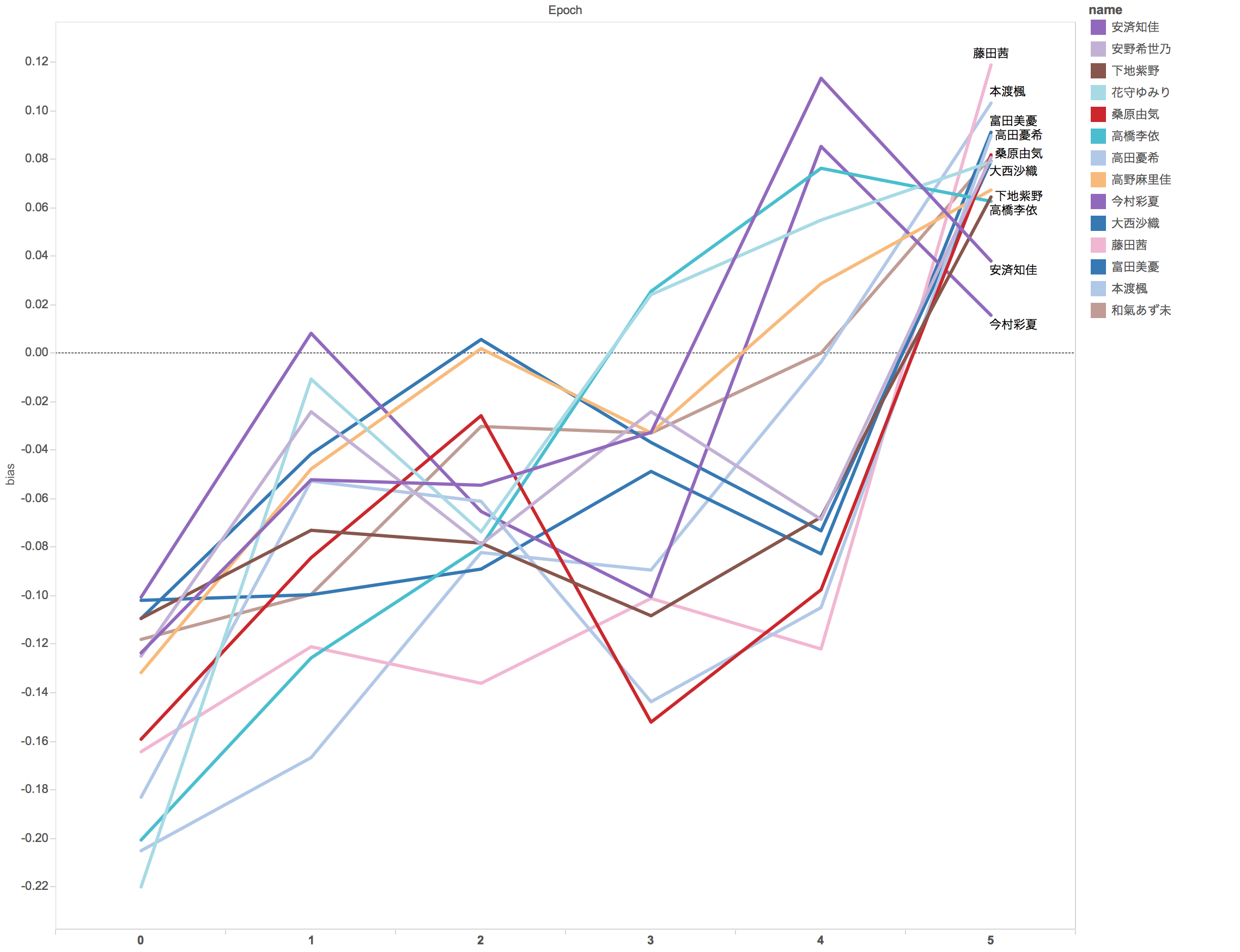
このデータ表現を使えば直近ブレイクした声優を探すこともできます。何人かピックアップしてみます。推し増しを検討されている方は参考にしてください。
特徴ベクトルのマッピング
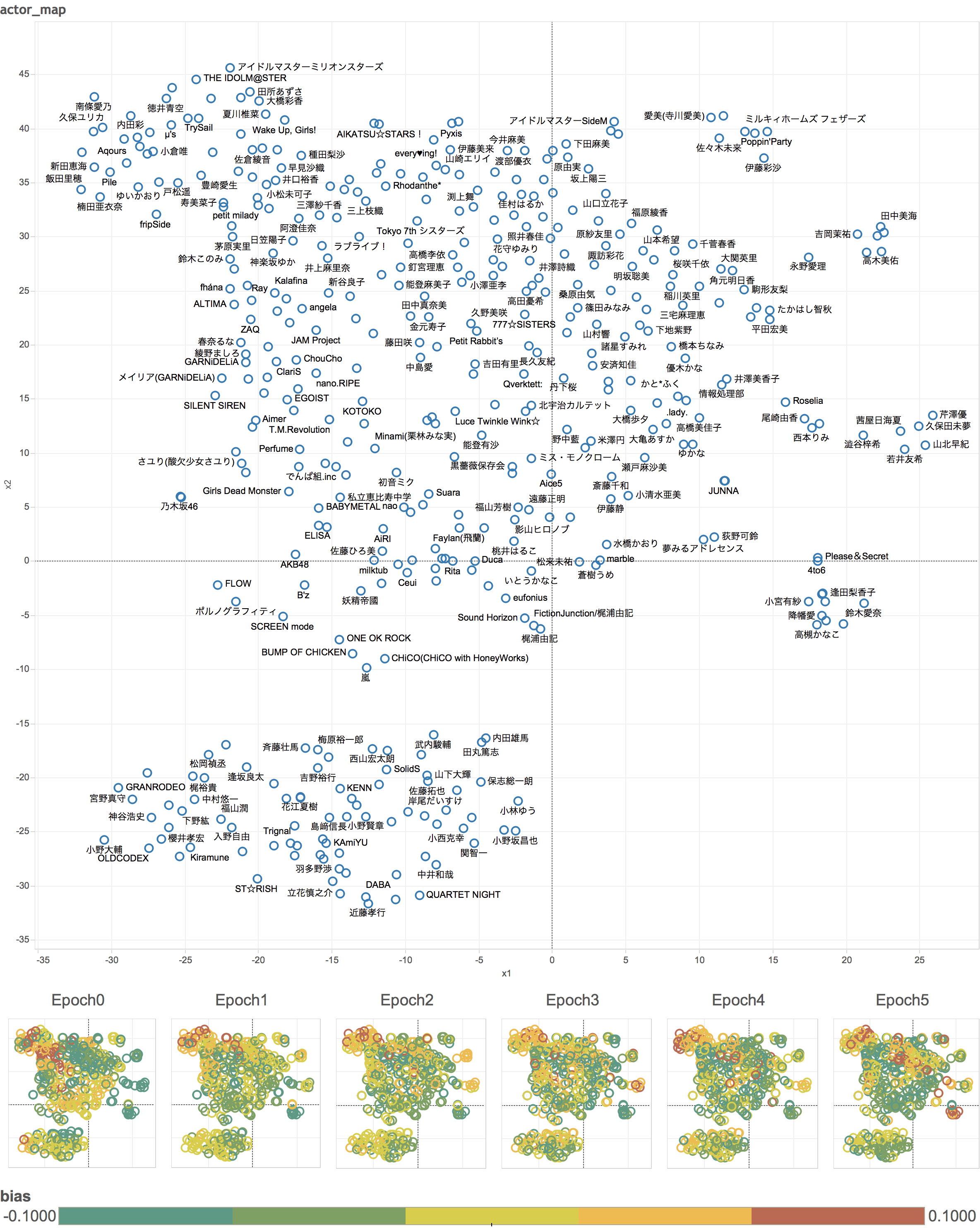
$\gamma_i$は各声優の特徴ベクトルです。これをt-SNEで2次元に圧縮してマッピングします。似ている声優同士が近くにマッピングされます。さらに、Epoch毎のバイアスの値を色で表現します。
こうしてみるといつどのクラスタが活気づいているのかが一目瞭然ですね。例えばAqoursのメンバー(第4象限の島)はEpoch5で急に目立つようになりました。
まとめ
- バイアスの時間発展を考慮したレコメンドアルゴリズムを実装してみました
- 声優の流行を可視化してみました
それでは、До свидания