Deep Learning for Audio Signal Processingという論文でDeep Learningにおける、音声をはじめとする時系列データの処理方法がまとめられていたので紹介したいと思います。
この記事で紹介するのは
- 1D Convolution
- Dialated 1D Convolution
- RNN
- Bi-directional RNN
- Attention
の5つです。
1D Convolution

上の図は入力時系列$x$が中間層$h$を通り、出力時系列$y$に変換される様子を表しています。
オレンジの破線は時刻$t-1$での出力$y_{t-1}$を計算する処理を表し、赤の実線は時刻$t$での出力$y_t$を表します。各ブロックは各層のセルの値を表します。
1D Convolution Layerでは各層のセルの値は前の層のセルと一次元のフィルタの畳み込みによって表されます。この図の例では3つの重みを持つフィルタを用いています。
形式的に書くと、例えば$h_t, y_t$の値は活性化関数を$\sigma$、バイアスを$b$とすると
h_t = \sigma(w_1^{(1)}x_{t-1} + w_2^{(1)}x_{t} + w_3^{(1)}x_{t+1} + b)\\
y_t = \sigma(w_1^{(2)}h_{t-1} + w_2^{(2)}h_{t} + w_3^{(2)}h_{t+1} + b)
のように計算できます。
Dialated 1D Convolution

Dialated 1D Convolutionではdialation $k$に従って畳み込みに使うセルを決めます。
この図の例では$h$から$y$への畳込み層で$k=2$としており、3つの重みを2時刻ずらしながら畳み込んでいます。なので$y$を計算する際には$h_{t-2}, h_t, h_{t+2}$が使われています。
$x$から$h$への畳み込み層では$k=1$としています。このようにDialated 1D Convolution Layerを用いる際は、入力側から$k$を$(1, 2, 4, \dots)$と増やしていくことで、入力層での受容野をより広く確保することが出来ます。
RNN

GRUやLSTMなどのRNNでは、隠れセル$h_t$は現時刻の入力$x_t$と1つ前の時刻の隠れセル$h_{t-1}$の値によって形式的に次のように計算できます。
ht = \tanh(w_h h_{t-1} + w_x x_t + b)
この計算は再帰的に行われ、勾配消失も起きやすくなるため通常は普通のRNNは用いずにGRUやLSTMが使われます。
RNNのより詳しい説明はゼロから作るDeep Learning 2がとてもわかりやすいのでそちらを参照してください。
Bi-directional RNN
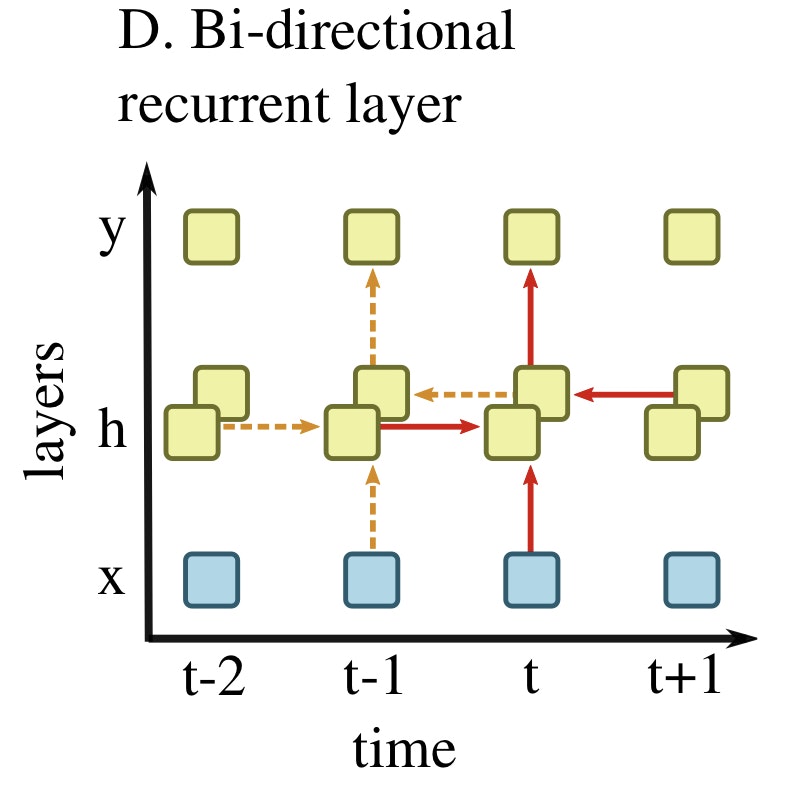
Bi-directional RNN(双方向RNN)では過去の隠れセルの情報だけでなく未来の隠れセルの情報も加味します。
未来の情報を用いるので、オンライン学習には使えません。
Attention

AttentionではEncoderとDecoderという機構を持ちます。それぞれに対応する埋め込み層$h_e$および$h_d$を持ち、コンテキスト$c$が橋渡し役として働きます。この図において、時刻$t$に対応するコンテキスト$c_t$はEncoderの埋め込み層のセル$h_{e, t-2}, h_{e, t-1}, h_{e, t}, h_{e, t+1}$の重み付け和で計算でき、その重みはDecoderの埋め込み層のセル$h_{d, t-1}$と計算に使われたEncoderの埋め込み層のセルの値から計算されます。この様子は図中の緑の点線で表されています。
最終的に$y_t$は1つ前の時刻$y_{t-1}$と1つ前の時刻のDecoderの埋め込み層のセル$h_{d, t-1}$とコンテキスト$c_t$によって計算されます。
この計算方法により、入力と出力の相関性を考慮することが出来ます。