ほぼほぼこの記事の翻訳です。
mAPは物体検知モデルに使われる評価指標です。mAPを理解するにはまずPrecision、Recall、IoUについて理解する必要があります。
Precision(適合率)
予測がどれだけ正確かを表す。
光の速さを知りたいとします。
何らかの検索システムで「光の速さ」で検索した結果、100件の文書がヒットしたとする。
その100件のうち、「光の速さ」が正しく分かる文書を正解とし、正解は60件だったとする。
すると、この場合の適合率は 60/100 = 0.60 となる。
Precision=\frac{TP}{TP+FP}
Recall(再現率)
結果として出てくるべきもののうち、実際出てきたものの割合
検索システムが扱う全データ(文書)の中で、光の速さが分かるものは全部で200件だとする。
しかし、「光の速さ」と検索して、実際に得られた結果(文書)は90件だとする。
すると、この場合の再現率は 90/200 = 0.45 となる。
Recall = \frac{TP}{TP + FN}
IoU(Intersection over Union)
予測結果とGround Truthがどれだけ重なっているかを表す。
閾値(0.5など)を設定し、予測がTrue PositiveかFalse Positiveかを判断する場合もある。

AP (Average Precision、平均適合率)

上の表は、5つのりんごを各画像に含むデータセットにおいて、モデルの予測結果を予測の信頼度順で並べたものである。
2つめのカラム(Correct?)は予測が正しいかを表す(この例では$IoU\geq0.5$で正しいとされる)
まず、Rankが3の列を例に、precisionとrecallがどのように計算されているかを見てみる。
-
Precision
画像内のりんごの領域を3つ予測したのに対し、実際は2つしか正しく予測できていない => 2/3 = 0.67 -
Recall
画像内に5つりんごがあるのに対し、正しく予測できているのは2つのみ => 2/5 = 0.4
Recallは表の下に行くほど上がるが、precisionはzigzagなパターンで動く。
これを可視化するために横軸にRecall、縦軸にPrecisionをとってプロットする
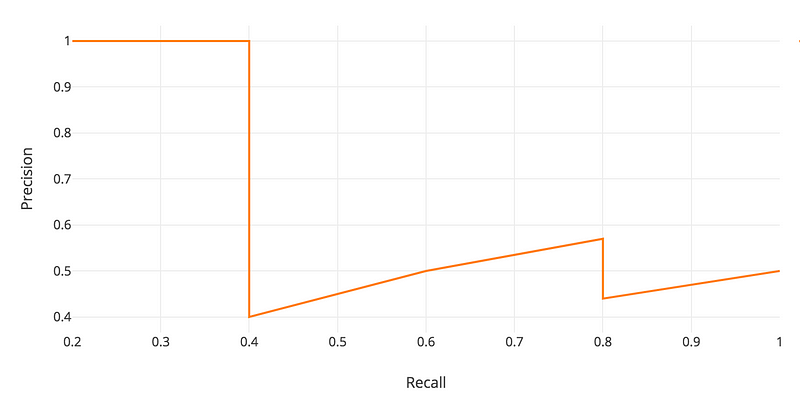
APの定義は、上のprecision-recall曲線の下の部分の面積である。
$$
AP = \int_0^1p(r)dr
$$
PrecisionとRecallは常に0から1の間値を取るため、APも常に0から1の間の値をとる。
APを物体検知について計算する前に、しばしば上のzigzagパターンをなだらかにする。
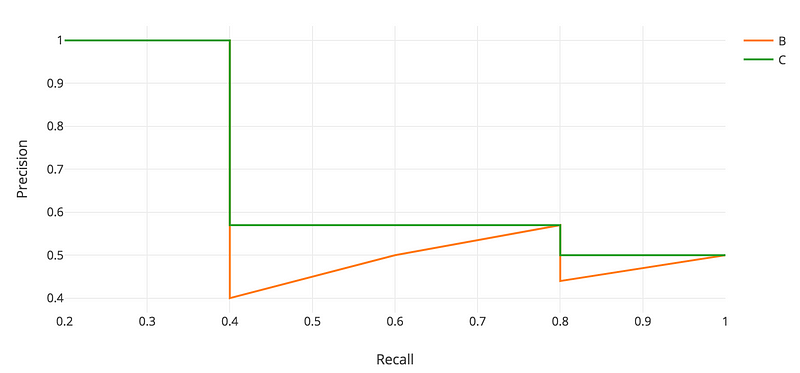
各recallの値に対して、右側にある一番大きいprecisionの値をとってきてそのrecallに対するprecisionの値と置き換える。

オレンジの線は緑の線に変換され、zigzagなパターンから単調に減少するパターンになる。
この変換により計算されたAPの値はランクのわずかな変動に対して安定するようになる。
数学的には、再現率$\tilde r$に対する適合率を、$\tilde r$より右側の範囲にある最大の適合率で置き換える。
p_{interp}(r) = \max_{\tilde r \geq r}p(\tilde r)
Interpolated AP(補完適合率)
PASCAL VOC challengeにおいて、予測は$IoU \geq 0.5$のときPositiveになる。また、同じ物体に対して複数の検出がなされた場合、一番最初の検出をPositiveとし、残りをNegativeとする。
Pascal VOC2008では、11点の補完適合率の平均が計算された。

具体的には、まずrecallの値を0から1.0まで11点に分ける(0, 0.1, 0.2, ..., 0.9, 1.0)。
次に、これら11個のrecallの値に対してmaximum precision value(上の$p_{iterp}(r)$)の平均を計算する。
AP = \frac{1}{11} \sum_{r \in (0.0, \dots, 1.0)}AP_r \\
= \frac{1}{11} \sum_{r \in (0.0, \dots, 1.0)}p_{iterp}(r) \\
= \frac{1}{11} (AP_r(0) + AP_r(0.1) + \dots + AP_r(1.0))
$AP_r$が非常に小さい時、残りの項も0であるとみなせ、recallが100%になるまで予測をする必要がないということがわかる。
PASCAL VOCにはクラスが20個ありAPはそれぞれのクラスに対して計算され、これらの平均がmAPとして算出される。
この手法には問題点が2つある。
- あまり正確ではない
- 低いAPに対しての手法の違いを測れない
よってPASCAL VOCは2008年以降、異なるAPの計算手法が採用されている。
COCO mAP
最新の研究ではCOCO datasetに対する結果のみ示す傾向がある。
- COCO mAPでは101点の補完適合率が計算に使われている。
- 複数のIoUの閾値に関しての平均をAPとしている。
- 例えばAP@[.5:.95]はステップサイズ0.05で0.5から0.95までのIoUのAPの平均をとっている。
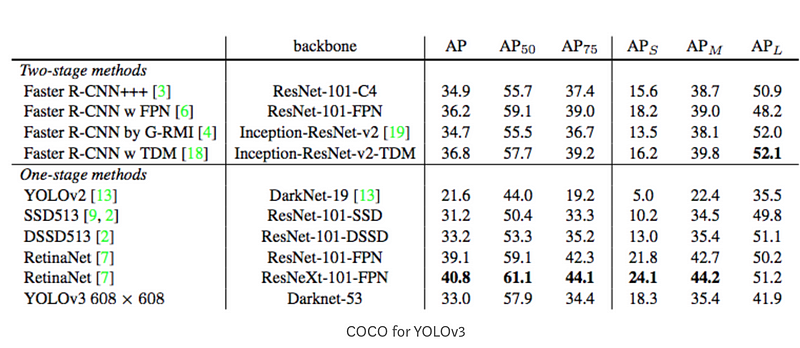
上の図の$AP_{75}$はIoU=0.75でのAPを表す。
mAPはAPの平均である。ある文脈では各クラスのAPを計算し、それらを平均する。しかし他の文脈ではAPとmAPは同じ場合もある。
参考
mAP (mean Average Precision) for Object Detection