総務省メールマガジン「M-ICTナウ:実装の進むAI・IoT」によると、今やAI・IoTは全ての日本企業のうち6割が何らかのプロセスで導入しているとのこと。そして物流業界は各業界の中でもIoTの導入が進む最たる分野です。
その物流業界で近年注目されているのがAGV。AGVとは、Automatic Guided Vehicleの略で、無人搬送車のことです。
AGVは、荷物を自動的に所定の場所へ運べるため、物流倉庫の自動化に欠かせないものです。しかし、導入する上では様々な問題があり、その内の一つが「AGV移動経路の最適化」。
現在、世界中で移動経路最適化問題の解決に向けて、様々な経路最適化アルゴリズムを利用した研究がなされています。
物流倉庫の自動化に最適なアルゴリズムは、まだ決まっていない
AGVの移動経路最適化問題については、決定版となるアルゴリズムは存在しないのが現状です。
現在、移動経路の決定において使えるアルゴリズムは複数存在します。それぞれのアルゴリズムの特徴は一長一短。AGVの移動経路決定においては、条件に応じてアルゴリズムを選択していくことになります。
AGVの経路最適化問題を解くには物流倉庫内のルール化がポイント
しかし、経路最適化のためのアルゴリズム選択といっても、何も考えない状態だと、AGVが自由に倉庫内を動き回れます。そのため、検討すべき内容が多くなりすぎてしまい、アルゴリズムの計算に時間を要する事態に陥りがち。
このような事態を回避するには、物流倉庫内のルール化がポイントです。例えば空間を区切る、ロボットの動きを制限するなど、ある程度の制約をAGVに与えることで、アルゴリズムの計算範囲も現実的な大きさに収められます。
AGVの経路最適化問題に使われるアルゴリズムとは
ここからは、AGVの経路最適化問題の解決によく使用されるアルゴリズムの特徴をみていきましょう。
遺伝的アルゴリズム
遺伝的アルゴリズムは、生物進化のシステムを真似たアルゴリズムです。経路問題を解く際には、経路の解一つひとつを「個体」と呼び、「選択淘汰」「交叉」「突然変異」の3つの動作を個体ごとに適用します。
この3つの動作で次世代に経路情報を残し、経路問題の解を求めていきます。
経路最適化問題を遺伝的アルゴリズムによって解く場合は、まず経路の分岐ごとに番号を割り振って、ランダムな経路を網羅的に生成します。
ただし、同じ番号の分岐を2回以上通過する場合は、経路がループしていることになり、最短経路とは呼べません。また、物理的に移動不可な分岐への移動が要求される場合も同様です。このような経路はアルゴリズム適用対象から除外します。
経路の生成が完了次第、それぞれの経路について選択淘汰から順に適用していきます。
1.選択淘汰
選択淘汰は、経路の解の中から法則に基づいた選択をし、次の世代に残す経路情報を決める動作です。
次の世代にいくつ経路情報を残すかは、問題によって検討する必要があります。
選択の方法はいくつかありますが、最も代表的なのは「ルーレット選択」。ルーレット選択のポイントは次のようなものです。
- それぞれの経路情報の評価値に応じて次世代に残る確率を決め、選択を実施
- 経路情報は、経路の総和が短いほど優秀といえるので、経路総和の逆数を評価値とすることが一般的
- 一番優秀である経路情報は、そのまま次世代に移行
- 一番優秀である経路情報が数世代にわたって変わらない場合は処理を終了
- 処理を終了するまでの世代数は要検討
もちろん、上記処理によって優秀でない経路情報が選択される可能性もあります。しかしながら、後述する「突然変異」により、非効率な経路が優秀な経路に化ける可能性も。多様性の維持という意味でも、非効率な経路を残すことを容認しています。
2.交叉
交叉は、生物が交配によって子孫を残していくシステムをモデルにした動作です。
先ほどの選択淘汰によって選ばれた経路から2つを選択し、経路情報を入れ替えます。交叉の方法も多種多様ですが、例えば次のような2つの経路が選択されたとします。
経路1:[1,4,15,9]
経路2:[3,16,2,8]
上記の赤色の数字を入れ替えます。
経路1´:[16,4,2,9]
経路2´:[3,1,15,8]
このように、遺伝子情報の交叉を模倣して、2つの経路情報を部分的に入れ替えます。
本来ならば、交叉させる番号はランダムに選ばなければなりません。しかし計算の効率を考えると、ループする経路や移動不可能な経路が生まれないよう考慮が必要になることも。また、交叉させる遺伝子はランダムに選択するほうがよいとされています。
3.突然変異
突然変異は、生物界での放射線や活性酸素等による遺伝子の切断などをモデルにした動作です。
経路最適化問題においては、経路情報の一部を低い確率でランダムに変化させます。例えば以下のように経路情報の青色部分が突然変異したとします。
経路3:[4,8,3,5]
経路3´:[4,8,6,5]
突然変異先の情報もランダムに決定します。この動作は、多様性の維持に重要な役割を果たす動作です。
この3つの動作を繰り返すことにより、最も優秀な経路情報を最適解に近づけていきます。
ダイクストラ法
ダイクストラ法は、最短経路問題を解くための最良優先探索によるアルゴリズム。重みづけされた辺によって各分岐を結んだ図上で、最もコストが小さくなるゴールまでの経路を導き出せます。
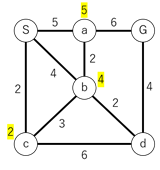
例えば、以下のような図を考えてみましょう。点Sがスタートで点Gがゴールです。各線についている数字は、その辺を通る際に要する移動コストを表しています。AGVの経路最適化問題を処理する場合は、距離や混雑具合でコストを算出するとよいでしょう。
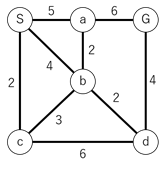
ダイクストラ法は、ある点に隣接する点へ移動するコストを計算し、別ルートで低いコストの経路が見つかれば、最低コストを更新。この処理を終点まで繰り返すことにより、最短経路を導き出せます。
なお、既に通った道を再度通ることは最短距離の考えから外れるため、なしとします。
それでは、実際に最短経路を導き出します。処理は次の順序で実施されます。
1.始点である点Sに隣接する点への移動コストを算出
2.点aに隣接する点への移動コストを算出
ここで終点の点Gへのコストが11と一旦算出される。点bへのコストは5+2=7と、既に出ているコスト4より多いため、最低コストの更新はしない。また、再度点Sへ戻るような経路は、一度通った経路であるため考慮しない
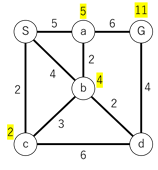
3.点b以下にも同様に隣接点への移動コスト算出を繰り返す
4.最低コストを下回るコストが出た場合は、最低コスト情報を適宜更新
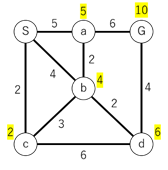
5.最終的にS→b→d→Gのコストが10と一番小さいことがわかる。
このように手続きを繰り替えすことで最短経路を求められます。しかしながら経路を全て探索することになるため、計算時間は他のアルゴリズムと比べて多くかかる傾向にあります。
A*(エースター)アルゴリズム
A*アルゴリズムは、「ヒューリスティック関数」と呼ばれる指標関数を用いて探索するアルゴリズム。
ヒューリスティック関数は、各ポイントからゴールまでの距離を計算。このゴールまでの距離は「推定コスト」と呼ばれ、「ゴールまでこれくらいの移動が必要」という数値を示します。
ヒューリスティック関数には状況に応じて様々な計算式が使われます。
例えば、シンプルな例として、斜め移動を許可した5×5の2次元グリッド中でのAGV移動を考えてみましょう。

今回は問題が単純なので、ヒューリスティック関数も単純です。
斜め移動が許可されているので、横軸の座標をx、縦軸の座標をyとすると、「(ゴールのx-スタートのx)か(ゴールのy-スタートのy)のどちらか多い方」がヒューリスティック関数です。
今回はどちらも「3」なので、スタートマスの推定コストは3になります。
スタートから対象マスまでの移動にかかるコストを「実コスト」、推定コスト+実コストをそのマスの「スコア」とします。このスコアが少ないマスを選択していくのが原則です。
実コストをC、推定コストをH、スコアをSとして、計算順番を①~③で示すと、以下のような形になります。
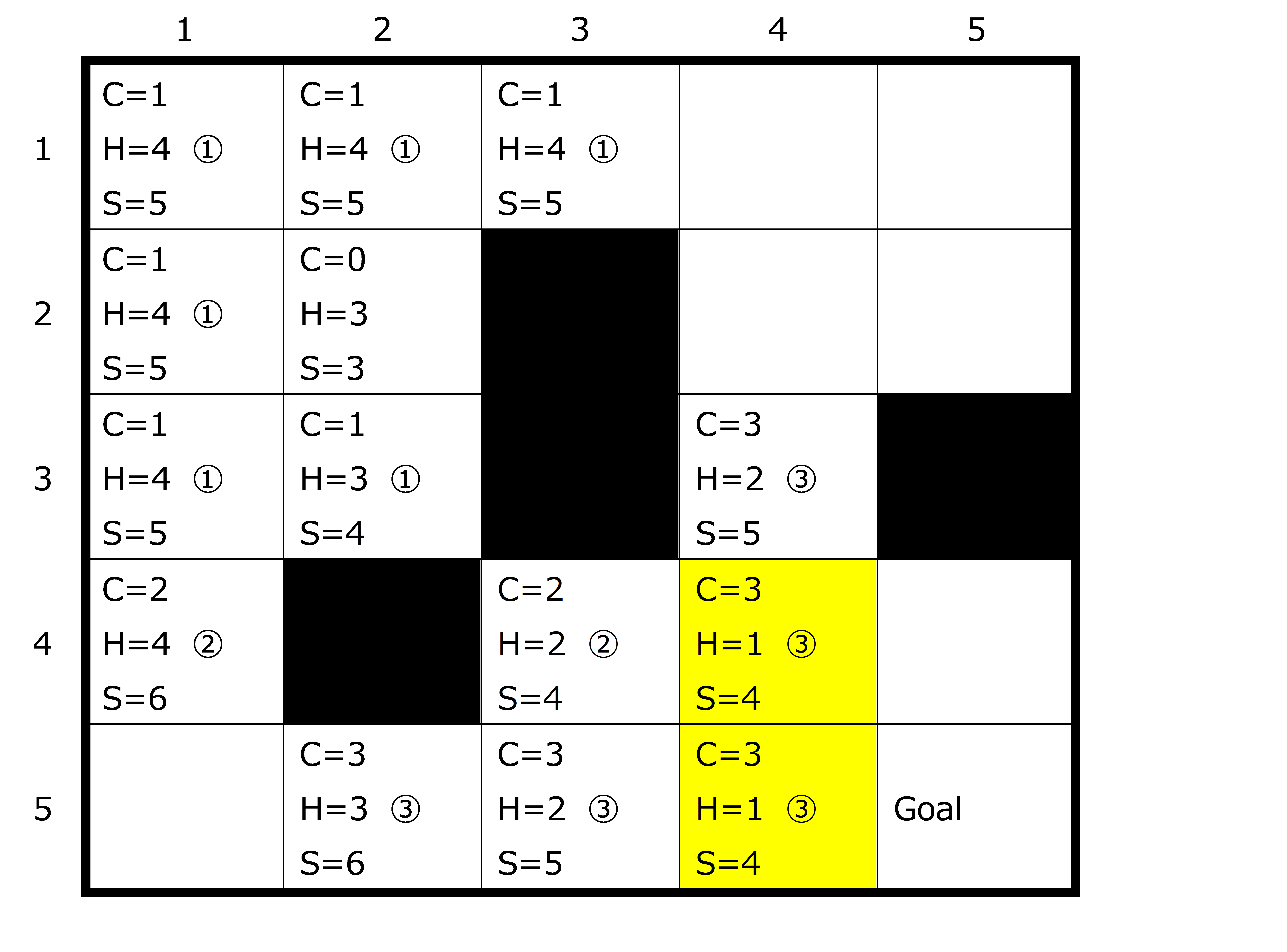
黄色マスはどちらを選んでもゴールできるので、どちらを選ぶかはプログラムの組み方次第です。
群知能アルゴリズム
群知能アルゴリズムとは、自然界における動物や昆虫の「群行動」を模倣したアルゴリズムです。個体の要素が相互作用しあって生まれた環境が、再び個体へ環境条件を与えるような振る舞いをアルゴリズムで再現しています。
群知能アルゴリズムは複数存在しますが、今回は「蟻コロニー最適化アルゴリズム(以下ACO)」を取り上げます。
蟻は餌場までの経路を移動する際にフェロモンを発生。後続の蟻はフェロモンを感知できる方の経路を選びます。フェロモンが複数感知できる場合は、よりフェロモンが強い経路を選択します。この動きを模倣したアルゴリズムがACOです。
例えば、AGVの経路選択アルゴリズムにACOを利用する場合は、このフェロモンを逆手にとって、交通量の少ない経路を選択するように設計します。
車道を通るコストは、「実質距離+交通密度」で計算されるのが一般的です。この交通密度を計算する際に、仮想フェロモンを使います。仮想フェロモンは一定時間でなくなりますが、頻繁に使用される経路は仮想フェロモンが継続して蓄積され、なかなか0になりません。
フェロモンを大量に蓄積している経路は、AGVの渋滞発生確率が高いことも。そのため、フェロモンを蓄積している経路は候補から外しやすいようにプログラムを設計するとよいでしょう。倉庫内を移動しやすくなる可能性が上がり、倉庫内のAGV作業効率UPに繋がります。
強化学習
ある環境内におけるエージェントに、行動を通じて報酬が最も多く得られるような方策(policy)を学習させるアルゴリズムを強化学習と呼びます。例えばゲームが環境であれば、エージェントはプレイヤーです。
強化学習においては、即時報酬の最大化は狙わず、将来的な行動価値の最大化を考慮して学習を進めます。この行動価値を「Q値」と呼びます。ここでは、このQ値を学習するアルゴリズムのうちの一つである「Q学習」についてお伝えします。
Q学習は、時間による報酬割引の概念を取り入れているため、Q値の学習に時間をかけすぎることはできません。報酬の時間割引を考慮し、報酬の総和を最大化することが目的です。
Q学習では環境の情報が一切与えられないので、ひたすら学習を試行する事態になることも。そのため、必然的に学習時間は多くなります。
一般的には、Q学習は次のようなポリシーで進みます。
・目的の状態に近づいた、もしくはなった時に正の報酬を受け取る
・正の報酬を受け取った場合は、その行動に到るまでの行動にも報酬を割り振る
・目的の状態から遠ざかった時に負の報酬を受け取る
・エージェントは、現在わかっている範囲で、一番高い価値になると思われる行動を選択する
しかしながら、上記内容だとエージェントが価値の高い行動しか起こそうとしなくなるので、行動をある程度ばらけさせる必要が出てきます。
そこで使われるのが、「ε-グリーディ法」。適当な値ε(0.3など)を決めておき、確率εだけランダムな行動をとらせ、確率1-εだけ価値が最大となる行動をとらせます。
この強化学習に、深層学習の要素を加えた「深層強化学習」と呼ばれるアルゴリズムもあります。よく略称でDQN(Deep Q Network)と呼ばれます。ニューラルネットワークの仕組みを使い、解を求めていきます。
焼きなまし法
焼きなまし法は、金属を熱して冷ますことによって、熱する前よりも結晶を安定した状態にしていく「焼きなまし動作」を模倣したアルゴリズム。現在の状態に近い状態の解を生成し、解を遷移し続けることで、最適解を探索します。
現在の状態に近い状態においての解を「近傍解」と呼び、この近傍解によって処理を変えることが焼きなまし法の基本動作です。例えば、経路最適化問題においての近傍解は、通過する分岐点を一つだけ変更した経路の解などを指します。
焼きなまし法の基本動作
近傍解が現在の解よりも良い場合:必ず選択する
近傍解が現在の解よりも悪い場合:温度パラメータと変化量によって選択するかどうか決定する
「温度パラメータ」は、仮想的な温度を表すパラメータで、処理回数の増加により下がっていくように設計します。温度が高い状態であれば、悪い解でも選択される可能性を増やし、温度が低ければ悪い解を選択されにくくします。
近傍解の変化量が大きい場合は悪い解が選択される確率を小さく、変化量が小さい場合は選択される確率を大きくします。
このような動作を取り入れることによって、局所的な最適解に留まりにくい状態を作りだせます。
タブーサーチ
タブーサーチは、「タブーリスト」と呼ばれるリストに解の変異を記録しながら探索をするアルゴリズム。近傍解を複数生成して、最終的に最もよい解を選択することが目的です。どの程度近傍解を生成し続けるかはプログラムの設定によります。
近傍解への移動がループすることを避けるため、既に遷移した解はタブーリストとして保持します。タブーリストに含まれる経路へ変異することは禁止です。また、タブーリストは解の探索を通じて更新されます。
AGVの経路最適化における各アルゴリズム性能比較
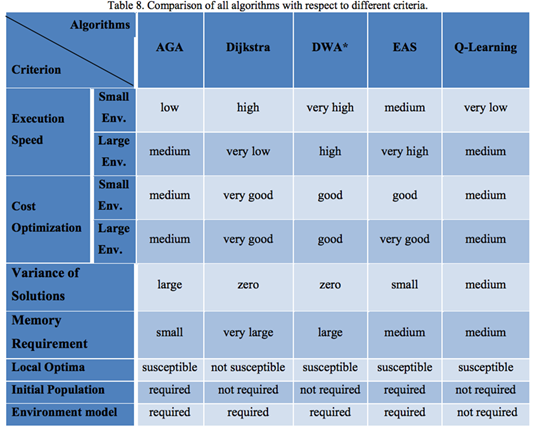
ここで、AGVの経路最適化における各アルゴリズムの性能を比較してみましょう。今回は次のアルゴリズムについてみていきます。
・Adaptive Genetic Algorithm(AGA)
遺伝的アルゴリズムに対して改良が加えられたアルゴリズム。交叉と突然変異確率に固定値を使用せず、個体数情報を使用して、多様性維持を考慮しつつ処理を進める。
・Dijkstra
既に解説済みのダイクストラ法
・Dynamic Weighting A*(DWA*)
A*アルゴリズムのヒューリスティック関数に重みづけをしたもの。初期段階の経路検索の削減、終盤の検索収束化を実現した。
・Elitist Ant System(EAS)
既に解説済みのACOの一種。短い経路は頻繁にアリが行き交う可能性が大きいという考え方に基づき、フェロモンの蓄積と蒸発の仕組みを改良した。
表の内容通り、どのアルゴリズムも一長一短であることが示されています。そのためAGV運用の環境や状況に応じて、適切なアルゴリズムを選択することが求められるのです。
アルゴリズムの検討には物流倉庫の業務全停止が必要なことも
アルゴリズムの選定には、AGVを運用する環境と同一の環境が必要不可欠。場合によっては物流倉庫の業務を全停止して、テストを複数回繰り返さなければいけない事態も容易に想定されます。
しかし、物流倉庫を全停止してまでアルゴリズムのテストを実施するような余裕は、どこの企業にもありません。
OPTIMUS AIなら3Dシミュレーターで物流倉庫内の業務を試行可能
Datumixが提供するOPTIMUS AIは、デジタルツイン+AI(=デジタルトリプレット)によって物流倉庫を3D再現。3D空間上でアルゴリズムのテストを行えるため、業務を停止することなく最適化検討が可能です。
DatumixのOPTIMUS AIは、次の6つのプロセスを通し、ワンストップで作業を自動化・効率化します。
1.現状把握
2.状況通知
3.提案
4.予測・推測
5.ミス予防・改善
6.自動化・効率化
費用も100万円からとリーズナブルで、最短3ヵ月で導入可能です。AGVの導入を検討されている方は、ぜひ一度Datumixへお声がけ下さい。