https://www.youtube.com/watch?v=i94OvYb6noo
上記リンクの講義で主張されているintuition重視の発想に感化されたので、例題としてweight normalization論文のbackpropagationの式をこの発想で導出してみました。
話を簡単にするために、重みは2次元ベクトルとしています。バイアス項は省きました。また、右端の出力$y$に非線形の関数を適用する部分も省いてあります。
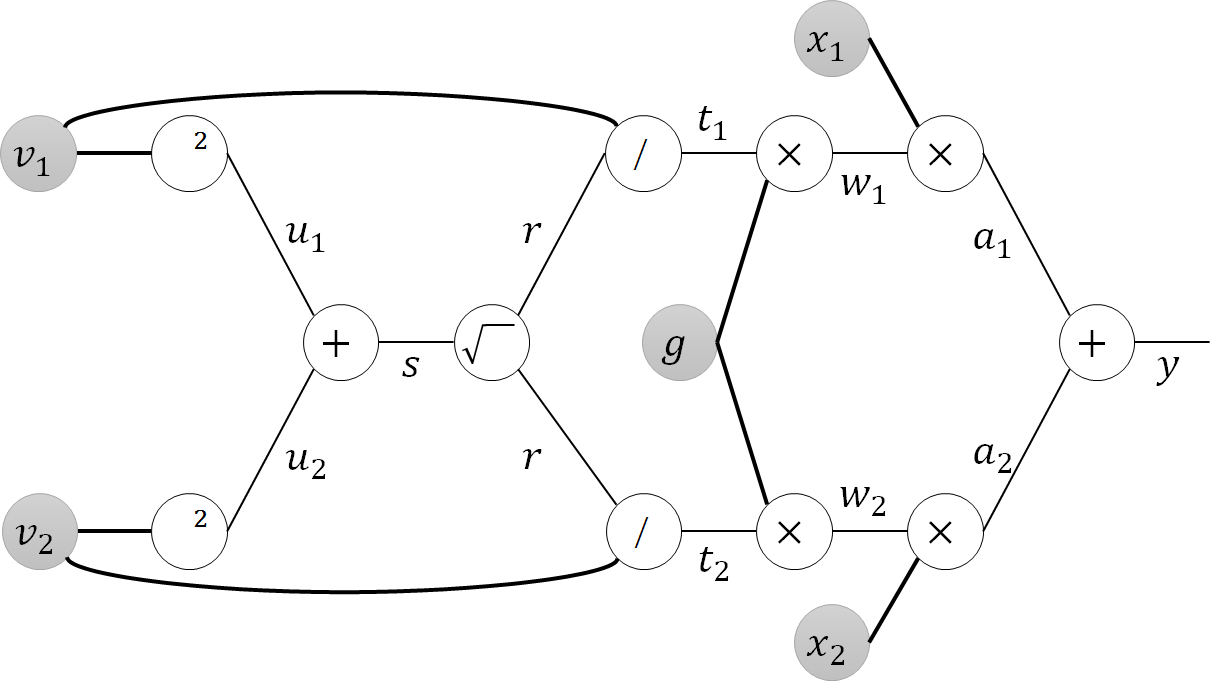
前向きの計算を書いておくと、以下のようになります。$\boldsymbol{v}$がweight normalization前の重み、$\boldsymbol{w}$がweight normalization後の重みです。$u$,$t$などの記号は適当に決めています。
$u_1=v_1^2$, $u_2 = v_2^2$
$s=u_1 + u_2$
$r={\sqrt s}$ ($\Vert \boldsymbol{v} \Vert$の計算)
$t_1 = v_1 / r$, $t_2 = v_2 / r$ (normalizationの計算)
$w_1 = gt_1$, $w_2 = gt_2$ ($g$は論文にあるとおり)
$a_1 = w_1 x_1$, $a_2 = w_2 x_2$
$y = a_1 + a_2$
では、lossを$L$として、$\frac{\partial L}{\partial y}$からスタートして、上図の右端から左へerrorをbackpropagateさせていきます。
$\frac{\partial L}{\partial a_1} = \frac{\partial L}{\partial y}\frac{\partial y}{\partial a_1}$
$y=a_1 + a_2$なので$\frac{\partial y}{\partial a_1}=1$。よって
$\frac{\partial L}{\partial a_1} = \frac{\partial L}{\partial y}\frac{\partial y}{\partial a_1}=\frac{\partial L}{\partial y}$
つまり、足し算は右からきたerrorを枝分かれさせてそのまま左へ送り出します。上述の講義では、足し算はgradient distributorだと言われています。
$a_2$についても同様です。
ひとつ左に移動します。
$\frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial a_1}\frac{\partial a_1}{\partial w_1}$
$a_1 = w_1 x_1$なので$\frac{\partial a_1}{\partial w_1} = x_1$。よって
$\frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial a_1}\frac{\partial a_1}{\partial w_1} = \frac{\partial L}{\partial a_1} x_1$
$w_2$についても同様です。また$x_1$については、
$\frac{\partial L}{\partial x_1} = \frac{\partial L}{\partial a_1}\frac{\partial a_1}{\partial x_1}$
$a_1 = w_1 x_1$なので$\frac{\partial a_1}{\partial x_1} = w_1$。よって
$\frac{\partial L}{\partial x_1} = \frac{\partial L}{\partial a_1}\frac{\partial a_1}{\partial x_1} = \frac{\partial L}{\partial a_1} w_1$
これが上述の講義でgradient "switcher"と呼ばれている、掛け算についてのbackpropagationです。
(なお、$x_1$や$x_2$が直前の層の出力である場合も、計算の仕方は変わりません。)
ところで論文に$\nabla_{\boldsymbol{w}}L$とあるのは、いま求めた$w_1$や$w_2$に関する偏微分のことです。つまり、
$\nabla_{\boldsymbol{w}}L = (\frac{\partial L}{\partial w_1} , \frac{\partial L}{\partial w_2}) = \frac{\partial L}{\partial y}\times(x_1, x_2) = \frac{\partial L}{\partial y} \boldsymbol{x}$
のことです。論文にas used normallyという表現(式(3)のすぐ下)がありますが、まさにそのとおりで、これは普通のbackpropagationでも計算する値です。
ひとつ左に移動します。
$\frac{\partial L}{\partial t_1} = \frac{\partial L}{\partial w_1}\frac{\partial w_1}{\partial t_1}$
$w_1 = gt_1$なので$\frac{\partial w_1}{\partial t_1}=g$。よって
$\frac{\partial L}{\partial t_1} = \frac{\partial L}{\partial w_1}\frac{\partial w_1}{\partial t_1} = \frac{\partial L}{\partial w_1} g$
$t_2$についても同様に
$\frac{\partial L}{\partial t_2} = \frac{\partial L}{\partial w_2}\frac{\partial w_2}{\partial t_2} = \frac{\partial L}{\partial w_2} g$
となります。
$g$については、前向きの計算で同じ$g$という値が枝分かれして使われているので、backpropagationでは右から合流してくるerrorをすべて加算します(この説明も上の動画にあります)。
$\frac{\partial L}{\partial g} = \frac{\partial L}{\partial w_1}\frac{\partial w_1}{\partial g} + \frac{\partial L}{\partial w_2}\frac{\partial w_2}{\partial g}
= \frac{\partial L}{\partial w_1} t_1 + \frac{\partial L}{\partial w_2} t_2$
この結果を、$\nabla_{\boldsymbol{w}}L$を使って書き直すと
$\frac{\partial L}{\partial g} = \nabla_{\boldsymbol{w}}L \cdot \boldsymbol{t}$
となります。$\cdot$は内積です。そして、上の図では$\boldsymbol{t} = \frac{\boldsymbol{v}}{\Vert \boldsymbol{v} \Vert}$としているので、
$\frac{\partial L}{\partial g} = \frac{ \nabla_{\boldsymbol{w}}L \cdot \boldsymbol{v}}{\Vert \boldsymbol{v} \Vert}$
となり論文の式(3)の左半分と一致します。
ひとつ左に移動します。
$r$については、前向きの計算で枝分かれして同じ値が使われているので、合流してくるerrorを加算します。
$\frac{\partial L}{\partial r} = \frac{\partial L}{\partial t_1}\frac{\partial t_1}{\partial r} + \frac{\partial L}{\partial t_2}\frac{\partial t_2}{\partial r}$
$t_1 = v_1 / r$と、上の結果を使うと
$\frac{\partial L}{\partial r} = - \frac{\partial L}{\partial w_1} g \frac{v_1}{r^2} - \frac{\partial L}{\partial t_2} g \frac{v_2}{r^2}$
ひとつ左に移動します。
$\frac{\partial L}{\partial s} = \frac{\partial L}{\partial r}\frac{\partial r}{\partial s}$
$r={\sqrt s}$より
$\frac{\partial L}{\partial s} = \frac{\partial L}{\partial r} \frac{1}{2r}$
ひとつ左に移動します。
$\frac{\partial L}{\partial u_1} = \frac{\partial L}{\partial s}\frac{\partial s}{\partial u_1} = \frac{\partial L}{\partial s}$
$u_2$についても同様です。
ひとつ左に移動します。
$v_1$, $v_2$は、それぞれ前向きの計算で同じ値が枝分かれして使われているので、合流してくるerrorを加算します。
$\frac{\partial L}{\partial v_1} = \frac{\partial L}{\partial u_1}\frac{\partial u_1}{\partial v_1} + \frac{\partial L}{\partial t_1}\frac{\partial t_1}{\partial v_1}$
$u_1 = v_1^2$より$\frac{\partial u_1}{\partial v_1} = 2 v_1$です。
また、$t_1 = \frac{v_1}{r}$より、$\frac{\partial t_1}{\partial v_1} = \frac{1}{r}$です。
$\frac{\partial L}{\partial t_1}$については、上のほうでおこなった計算に戻ると分かるので
$\frac{\partial L}{\partial v_1} = \frac{\partial L}{\partial u_1}\frac{\partial u_1}{\partial v_1} + \frac{\partial L}{\partial t_1}\frac{\partial t_1}{\partial v_1}
= 2 \frac{\partial L}{\partial s} v_1 + \frac{\partial L}{\partial w_1} g \frac{1}{r}$
となります。この式を、これまでの結果を使って書き直すと、次のようになります。
\begin{align}
\frac{\partial L}{\partial v_1}
& = 2 \frac{\partial L}{\partial s} v_1 + \frac{\partial L}{\partial w_1} g \frac{1}{r} \\
& = 2 \frac{\partial L}{\partial r} \frac{1}{2r} v_1 + \frac{\partial L}{\partial w_1} \frac{g}{r} \\
& = - \bigg(\frac{\partial L}{\partial w_1} g \frac{v_1}{r^2} + \frac{\partial L}{\partial t_2} g \frac{v_2}{r^2} \bigg) \frac{1}{r} v_1 + \frac{\partial L}{\partial w_1} \frac{g}{r} \\
& = - \bigg(\frac{\partial L}{\partial w_1} g \frac{v_1}{r} + \frac{\partial L}{\partial t_2} g \frac{v_2}{r}\bigg) \frac{1}{r^2} v_1 + \frac{\partial L}{\partial w_1} \frac{g}{r} \\
& = - \bigg(\frac{\partial L}{\partial w_1} t_1 + \frac{\partial L}{\partial t_2} t_2\bigg) \frac{g}{r^2} v_1 + \frac{\partial L}{\partial w_1} \frac{g}{r} \\
& = - \frac{\partial L}{\partial g} \frac{g}{r^2} v_1 + \frac{\partial L}{\partial w_1} \frac{g}{r}
\end{align}
$v_2$に関する偏微分も同様に
$\frac{\partial L}{\partial v_2} = - \frac{\partial L}{\partial g} \frac{g}{r^2} v_2 + \frac{\partial L}{\partial w_2}\frac{g}{r}$
となります。$v_1$と$v_2$に関する結果をまとめて書くと
$\frac{\partial L}{\partial \boldsymbol{v}} = - \frac{\partial L}{\partial g} \frac{g}{r^2} \boldsymbol{v} + \frac{\partial L}{\partial \boldsymbol{w}}\frac{g}{r}$
となります。
$r=\Vert \boldsymbol{v} \Vert$だったので、
$\nabla_\boldsymbol{v} L = - \frac{g \nabla_g L}{\Vert \boldsymbol{v} \Vert^2} \boldsymbol{v} + \frac{g}{\Vert \boldsymbol{v} \Vert} \nabla_\boldsymbol{w} L$
となり、これは論文の式(3)の右半分に一致します。