混合正規分布モデルのパラメータをあえてvariational optimizationで推定してみる

はじめに

前回、階段関数の最小値をvariational optimizationで求めてみました。
しかし、階段関数の最小化という問題設定が、ちょっと単純すぎました。

そこで今回は、2つの1変数正規分布の混合モデルを扱います。
この混合モデルのパラメータを、variational optimizationで推定してみます。

モデル

今回扱うのは、2つの1変数正規分布の混合分布モデルです。
2つの正規分布の平均パラメータと標準偏差パラメータを、それぞれ$(\mu_1, \sigma_1)$, $(\mu_0, \sigma_0)$とします。

1と0の値を等確率で与えるベルヌーイ分布から値をdrawし、
1であれば$\mathcal{N}(\mu_1, \sigma_1)$から値をdraw、0であれば$\mathcal{N}(\mu_0, \sigma_0)$から値をdrawします。つまり

\begin{align}
z & \sim \mbox{Bernoulli}(1/2, 1/2) \\
x & \sim \mathcal{N}(\mu_z, \sigma_z)
\end{align}

というのが今回扱うモデルです。観測データを、この混合分布によってモデル化します。
そして、与えられた観測データを良く表すような$(\mu_1, \sigma_1)$, $(\mu_0, \sigma_0)$を推定します。

観測データの集合を$\boldsymbol{x} = \{ x_1, \ldots, x_N \}$とすると、対数周辺尤度は以下のように書けます。

\begin{align}
\log p(\boldsymbol{x}) = \sum_{i=1}^N \log \sum_{z_i \in \{ 0, 1\}} p(x_i | z_i) p(z_i)
\end{align}

もちろん、このモデルのパラメータ推定には普通にEMアルゴリズムを使えばいいのですが、
今回はあえて、variational optimizationで推定をしてみます。

ポイントは、$z$が離散値をとる隠れ変数であることです。

対数周辺尤度のlower bound

個々の観測データ$x_i$の対数周辺尤度について、

\begin{align}
\log p(x_i) & = \log \sum_{z_i \in \{ 0, 1\}} p(x_i | z_i) p(z_i) \\
& = \log \sum_{z_i \in \{ 0, 1\}} q(z_i|x_i) \frac{p(x_i | z_i) p(z_i)}{q(z_i|x_i)} \\
& \geq \sum_{z_i \in \{ 0, 1\}} q(z_i|x_i) \log \frac{p(x_i | z_i) p(z_i)}{q(z_i|x_i)} \\
& = \mathbb{E}_q [ \log p(x_i | z_i) ] + \mathbb{E}_q [ \log p(z_i) ] - \mathbb{E}_q [ \log q(z_i | x_i) ]  
\end{align}

と、Jensenの不等式を使うことによってlower boundを求めることができます。
そして、このlower boundを最大化することによって、混合モデルのパラメータを推定します。
ここまでは通常通りです。

このlower boundには3つの項が含まれます。

• $\mathbb{E}_q [ \log p(x_i | z_i) ]$

• $\mathbb{E}_q [ \log p(z_i) ]$

• $- \mathbb{E}_q [ \log q(z_i | x_i) ]$

なお、今回は$p(z_i)$について$0$が出る確率も$1$が出る確率も同じ$1/2$と仮定しますので、
2番目の項$\mathbb{E}_q [ \log p(z_i) ]$は定数になり、lower boundの最大化をするにあたっては無視できます。

今回の解き方：離散隠れ変数をそのまま使う

ここから、あえて問題を解きにくくします。
$\log p(x_i | z_i)$を、次のように、$z_i$の離散的な値をそのまま使うかたちで書き下します。

\begin{align}
\log p(x_i | z_i)
& =
z_i \log \bigg[ \frac{1}{\sqrt{2 \pi \sigma_1^2}} \exp\Big(- \frac{(x_i - \mu_1)^2}{2\sigma_1^2}\Big) \bigg]
+
(1 - z_i) \log \bigg[ \frac{1}{\sqrt{2 \pi \sigma_0^2}} \exp\Big(- \frac{(x_i - \mu_0)^2}{2\sigma_0^2}\Big) \bigg]
\end{align}

そして、対数周辺尤度のlower boundにあった1つめの項を、これの$q(z_i|x_i)$に関する期待値だ、と見なします。

離散分布のreparameterization

次に、$q(z_i|x_i)$については、$x_i$の値によって$1$の出る確率$\theta$が変わるベルヌーイ分布だと仮定します。
具体的には、$1$の出る確率$\theta$を、次のような$x$の関数で表すことにします。

\begin{align}
\theta(x) = \frac{1}{1 + e^{- (ax + b)}}
\end{align}

これはロジスティック回帰の式と同じ式です。

この$\theta$を$1$が出る確率と考えるので、$z$は$\theta$を使って以下のようにreparameterizeできることになります。

\begin{align}
z \equiv g(\epsilon ; \theta)
=
\begin{cases}
    1 & \mbox{if $\epsilon - \theta < 0$} \\
    0 & \mbox{if $\epsilon - \theta \geq 0$}
  \end{cases}
\end{align}

ここで、$\epsilon$は$[0,1)$の一様乱数です。

以上により、変分オートエンコーダについて議論するときに出てくるreparameterizationと同様に、
$\theta$というパラメータを使って、$\epsilon$というノイズ分布からのサンプルを変換することで、
$z$という本来扱いたかった値を書き直しています。
つまり、一様分布からのサンプルを使って、ベルヌーイ分布をreparameterizeしています。

しかし、関数$g(\epsilon ; \theta)$が$\theta$で微分できません！！！

ここが今回のポイントです。

この$g(\epsilon ; \theta)$が$\theta$で微分できないから、variational optimizationを使うのです。

繰り返しになりますが、今回扱っている問題は、実際には普通にEMアルゴリズムで解けます。
しかし、あえて問題を難しくして解いています。

lower boundのまとめ

上のほうで挙げたlower boundの3つの項のうち、3つめの$- \mathbb{E}_q [ \log q(z_i | x_i) ]$は、

\begin{align}
q(z_i | x_i)
= z_i \log \theta(x_i)
+ (1 - z_i) \log (1 - \theta(x_i))
\end{align}

これの$q$に関する期待値にマイナスを付けたものです。やはり$z_i$をそのまま使っています。

以上の議論より、観測データ$z_i$の対数周辺尤度のlower boundは、以下のようになります。

\begin{align}
& \mathbb{E}_q [ \log p(x_i | z_i) ] + \mathbb{E}_q [ \log p(z_i) ] - \mathbb{E}_q [ \log q(z_i | x_i) ]
\notag \\
& \approx
\mathbb{E}_q \bigg[
z_i \log \bigg[ \frac{1}{\sqrt{2 \pi \sigma_1^2}} \exp\Big(- \frac{(x_i - \mu_1)^2}{2\sigma_1^2}\Big) \bigg]
+
(1 - z_i) \log \bigg[ \frac{1}{\sqrt{2 \pi \sigma_0^2}} \exp\Big(- \frac{(x_i - \mu_0)^2}{2\sigma_0^2}\Big) \bigg]
\notag \\ & 
+ z_i^{(s)} \log \theta(x_i)
+ (1 - z_i^{(s)}) \log (1 - \theta(x_i)) \bigg] + const. 
\end{align}

これを、変分オートエンコーダの時と同様、モンテカルロ近似すると、以下のようになります。

\begin{align}
& \mathbb{E}_q [ \log p(x_i | z_i) ] + \mathbb{E}_q [ \log p(z_i) ] - \mathbb{E}_q [ \log q(z_i | x_i) ]
\notag \\
& \approx
\frac{1}{S} \sum_{s=1}^S \bigg\{
z_i^{(s)} \log \bigg[ \frac{1}{\sqrt{2 \pi \sigma_1^2}} \exp\Big(- \frac{(x_i - \mu_1)^2}{2\sigma_1^2}\Big) \bigg]
+
(1 - z_i^{(s)}) \log \bigg[ \frac{1}{\sqrt{2 \pi \sigma_0^2}} \exp\Big(- \frac{(x_i - \mu_0)^2}{2\sigma_0^2}\Big) \bigg]
\notag \\ & 
+ z_i^{(s)} \log \theta(x_i)
+ (1 - z_i^{(s)}) \log (1 - \theta(x_i)) \bigg\} + const. 
\end{align}

なお、$z_i^{(s)}$は$q(z_i | x_i)$からdrawしたサンプルの$s$番目、という意味です。

ポイントは、$z = g(\epsilon ; \theta)$というreparameterizationによって$z$が$\theta$に依存しているのに、
上のlower boundを$\theta$で微分できない、ということです。

$\theta$で微分できないので、当然、$\theta$の定義式に表れる傾きパラメータ$a$でも、切片パラメータ$b$でも、微分できません。

そこで、上の関数を最大化するために、variational optimizationを使います。

コード（PyTorchを使用）

ここからはコードで説明します。
以下が、上で定式化した問題をvariational optimizationで解くためのコードです。

variational optimizationが何なのかについては、前回の記事で紹介した論文¹を参考にしてください。

import numpy as np
import torch
from torch.distributions import Normal

def log(x):
  return torch.log(x + 1e-30)

np.random.seed(12)
torch.manual_seed(12)

m_a = torch.randn(1, requires_grad=True)
log_s_a = torch.zeros(1, requires_grad=True)
m_b = torch.randn(1, requires_grad=True)
log_s_b = torch.zeros(1, requires_grad=True)
opt_prop = torch.optim.Adam([m_a, log_s_a, m_b, log_s_b], lr=0.1)

mu1 = torch.randn(1, requires_grad=True)
log_s1 = torch.zeros(1, requires_grad=True)
mu0 = torch.randn(1, requires_grad=True)
log_s0 = torch.zeros(1, requires_grad=True)
opt_lh = torch.optim.Adam([mu1, log_s1, mu0, log_s0], lr=0.1)

true_mean = torch.tensor([10.0, 0.0])
true_std = torch.tensor([0.1, 0.1])

def observed_data(x_num):
  z = torch.tensor(np.random.randint(2, size=x_num))
  return torch.normal(true_mean[z], true_std[z])

post_sample_size = 2
prop_sample_size = 5
for i in range(1, 2001):

  # observed data
  x = observed_data(10)

  # proposal samples
  norm_a = Normal(m_a, torch.exp(log_s_a))
  norm_b = Normal(m_b, torch.exp(log_s_b))
  a_sample = norm_a.sample((prop_sample_size,))
  b_sample = norm_b.sample((prop_sample_size,))
  theta = 1 / (1 + torch.exp(-(a_sample * x + b_sample))).unsqueeze(2)

  # approx posterior samples
  epsilon = torch.rand((post_sample_size,))
  z = (epsilon - theta < 0.0).float().mean(dim=2)

  # negative ELBO
  norm1 = Normal(mu1, torch.exp(log_s1))
  norm0 = Normal(mu0, torch.exp(log_s0))
  loss = - z * norm1.log_prob(x) - (1 - z) * norm0.log_prob(x)
  loss.mean().backward()
  opt_lh.step()
  opt_lh.zero_grad()

  # variational optimization
  norm1 = Normal(mu1, torch.exp(log_s1))
  norm0 = Normal(mu0, torch.exp(log_s0))
  loss = - z * norm1.log_prob(x) - (1 - z) * norm0.log_prob(x)
  loss = loss.detach()
  theta = theta.squeeze()
  loss = loss + z * log(theta) + (1 - z) * log(1 - theta)
  temp = norm_a.log_prob(a_sample) + norm_b.log_prob(b_sample)
  loss = temp * loss
  loss = loss.mean()
  loss.backward()
  opt_prop.step()
  opt_prop.zero_grad()

  if i % 50 == 0:
    print('{:d} {:.4f} ; mu {:.4f} {:.4f} ;'.format(i, loss, mu1.item(), mu0.item()), end=' ')
    print('a {:.4f} {:.4f} ;'.format(m_a.item(), torch.exp(log_s_a).item()), end=' ')
    print('b {:.4f} {:.4f} ;'.format(m_b.item(), torch.exp(log_s_b).item()))

以下、このコードの各箇所について説明します。

提案分布のパラメータ

m_a = torch.randn(1, requires_grad=True)
log_s_a = torch.zeros(1, requires_grad=True)
m_b = torch.randn(1, requires_grad=True)
log_s_b = torch.zeros(1, requires_grad=True)
opt_prop = torch.optim.Adam([m_a, log_s_a, m_b, log_s_b], lr=0.1)

この箇所では、提案分布のパラメータを準備しています。提案分布は、variational optimizationで使う分布です。
標準偏差パラメータは、その対数でパラメータ化しています。これは常套手段です。

今回は、$\theta$を表すための$a$と$b$について、それぞれ正規分布$\mathcal{N}(m_a, s_a)$, $\mathcal{N}(m_b, s_b)$に従うと仮定します。
これら2つの正規分布が提案分布になります。

最適化アルゴリズムはSGDよりもAdamが良いようです。

混合モデルのパラメータ

mu1 = torch.randn(1, requires_grad=True)
log_s1 = torch.zeros(1, requires_grad=True)
mu0 = torch.randn(1, requires_grad=True)
log_s0 = torch.zeros(1, requires_grad=True)
opt_lh = torch.optim.Adam([mu1, log_s1, mu0, log_s0], lr=0.1)

この箇所では、混合正規分布モデルの2つのコンポーネントのパラメータを準備しています。
これら$(\mu_1, \sigma_1)$, $(\mu_0, \sigma_0)$が、値を知りたいパラメータです。

観測データの生成

true_mean = torch.tensor([10.0, 0.0])
true_std = torch.tensor([0.1, 0.1])

def observed_data(x_num):
  z = torch.tensor(np.random.randint(2, size=x_num))
  return torch.normal(true_mean[z], true_std[z])

この箇所では、観測データを生成する関数を定義しています。
ここにあるように、モデルパラメータの正解は$\mu_0 = 10$, $\mu_1 = 0$, $\sigma_0 = \sigma_1 = 0.1$です。
平均が離れていて、しかも標準偏差が小さいですので、解きやすいです（笑）。

2つのコンポーネントは等確率で選択されています。

サンプルの個数

post_sample_size = 2
prop_sample_size = 5

ここで、2種類のサンプルサイズを定義しています。
$q$からdrawするサンプルの個数post_sample_sizeと、
提案分布からdrawするサンプルの個数prop_sample_sizeです。

$q$からdrawするサンプルの個数は、lower boundをモンテカルロ近似するためのサンプルの個数です。
提案分布からdrawするサンプルの個数は、variational optimizationの計算に使うサンプルの個数です。
混乱しないようにしてください。

これらを組み合わせて、かつ、複数の観測データをミニバッチとして使いますので、
計算の途中経過は3階のテンソルで表されます。この点、ちょっとだけややこしいです。
コードではunsqueeze()やsqueeze()を使って適切に処理していますが、細かい説明は省きます。

次から最適化計算のforループの中に入ります。

データとサンプルの取得

  # observed data
  x = observed_data(10)

  # proposal samples
  norm_a = Normal(m_a, torch.exp(log_s_a))
  norm_b = Normal(m_b, torch.exp(log_s_b))
  a_sample = norm_a.sample((prop_sample_size,))
  b_sample = norm_b.sample((prop_sample_size,))
  theta = 1 / (1 + torch.exp(-(a_sample * x + b_sample))).unsqueeze(2)

  # approx posterior samples
  epsilon = torch.rand((post_sample_size,))
  z = (epsilon - theta < 0.0).float().mean(dim=2)

観測データを10個とってきてミニバッチとします。
そして、提案分布からのサンプル、期待値をモンテカルロ近似するためのサンプルを、取得しています。

モンテカルロ近似のためのサンプルを取得した後で、
すぐにそれを離散変数$z$の値に変換しています。ここが微分できない関数になっています。

モデルパラメータの更新

  # negative ELBO
  norm1 = Normal(mu1, torch.exp(log_s1))
  norm0 = Normal(mu0, torch.exp(log_s0))
  loss = - z * norm1.log_prob(x) - (1 - z) * norm0.log_prob(x)
  loss.mean().backward()
  opt_lh.step()
  opt_lh.zero_grad()

PyTorchを使っているので、問題を最小化問題にする必要があります。
ここではlower boundの符号を反転したものを求めています。
そして、勾配を求めて、モデルパラメータのほうだけを更新しています。

モデルパラメータと、提案分布のパラメータを同時に更新してしまうと、うまくいかないようです。

提案分布のパラメータの更新

  # variational optimization
  norm1 = Normal(mu1, torch.exp(log_s1))
  norm0 = Normal(mu0, torch.exp(log_s0))
  loss = - z * norm1.log_prob(x) - (1 - z) * norm0.log_prob(x)
  loss = loss.detach()
  theta = theta.squeeze()
  loss = loss + z * log(theta) + (1 - z) * log(1 - theta)
  temp = norm_a.log_prob(a_sample) + norm_b.log_prob(b_sample)
  loss = temp * loss
  loss = loss.mean()
  loss.backward()
  opt_prop.step()
  opt_prop.zero_grad()

ここで、variational optimizationで使っている提案分布のパラメータを更新しています。
loss = loss.detach()として、モデルパラメータへとバックプロパゲーションが影響しないようにしています。

実行結果例

以下に実行結果の例を示します。これは上のコードをGoogle Colabで動かした結果です。

50 -12.2363 ; mu 2.1934 2.1903 ; a 1.1447 2.0974 ; b -2.1215 2.2232 ;
100 -13.1802 ; mu 2.8875 2.2800 ; a 1.4094 1.4827 ; b -1.9289 2.2318 ;
150 -15.2190 ; mu 4.0622 2.2927 ; a 1.5273 1.5493 ; b -2.0697 2.4873 ;
200 -12.2075 ; mu 5.3152 2.2542 ; a 1.3106 2.3056 ; b -1.9884 3.4157 ;
250 -15.5192 ; mu 5.7899 2.4309 ; a 1.0140 2.1587 ; b -2.6235 4.3093 ;
300 -12.6226 ; mu 6.5151 2.6199 ; a 0.9809 1.8941 ; b -2.4376 3.4753 ;
350 -11.9939 ; mu 7.0813 2.7831 ; a 1.3452 1.6818 ; b -2.3017 3.5470 ;
400 -6.6383 ; mu 7.8392 2.2320 ; a 1.9958 0.6035 ; b -2.7098 1.5629 ;
450 -2.9759 ; mu 9.1602 0.9423 ; a 3.0399 0.2404 ; b -3.7323 1.4515 ;
500 -2.3072 ; mu 9.5306 -0.0496 ; a 2.6327 0.1423 ; b -4.0704 1.3669 ;
550 -0.3746 ; mu 9.9733 0.0309 ; a 3.4354 0.1125 ; b -5.0024 1.1865 ;
600 -0.2478 ; mu 9.9237 -0.0046 ; a 5.6454 0.0466 ; b -5.8097 1.3185 ;
650 -0.0095 ; mu 9.9744 -0.0723 ; a 4.8200 0.0397 ; b -5.9831 0.7193 ;
700 0.8780 ; mu 9.5248 -0.0097 ; a 3.0978 0.2189 ; b -7.8042 0.0829 ;
750 0.2440 ; mu 9.8618 0.0809 ; a 2.9898 0.2540 ; b -7.9245 0.0735 ;
800 0.4720 ; mu 9.9731 -0.1389 ; a 2.9887 0.2592 ; b -7.7430 0.0737 ;
850 -0.3429 ; mu 9.9955 0.0238 ; a 3.0051 0.2409 ; b -7.8025 0.0741 ;
900 -0.0313 ; mu 9.9997 0.0722 ; a 3.0030 0.2436 ; b -7.7243 0.0753 ;
950 -0.0474 ; mu 10.0098 0.0346 ; a 2.9789 0.2461 ; b -7.7649 0.0756 ;
1000 -0.4971 ; mu 9.9882 0.0070 ; a 2.9629 0.2410 ; b -7.5935 0.0765 ;
1050 -1.1353 ; mu 9.9924 -0.0322 ; a 2.9675 0.2272 ; b -7.4946 0.0760 ;
1100 -0.3819 ; mu 9.9775 -0.0118 ; a 2.9381 0.2091 ; b -7.3699 0.0757 ;
1150 -0.7562 ; mu 9.9989 -0.0381 ; a 2.9535 0.1983 ; b -7.3489 0.0777 ;
1200 -0.5896 ; mu 9.9725 0.0100 ; a 2.9614 0.2217 ; b -7.5616 0.0773 ;
1250 -0.9259 ; mu 9.9497 -0.0300 ; a 3.0379 0.2175 ; b -7.5249 0.0761 ;
1300 -1.2390 ; mu 10.0275 0.0312 ; a 3.0349 0.1944 ; b -7.1900 0.0754 ;
1350 -1.6943 ; mu 9.9672 -0.0324 ; a 3.0399 0.1972 ; b -7.2986 0.0712 ;
1400 -1.3874 ; mu 10.0143 0.0161 ; a 2.8871 0.2055 ; b -6.7051 0.0714 ;
1450 -0.8897 ; mu 10.0146 -0.0296 ; a 2.8770 0.2065 ; b -6.3173 0.0723 ;
1500 -1.5072 ; mu 9.9737 -0.0558 ; a 2.9733 0.2034 ; b -5.8202 0.0761 ;
1550 -0.9254 ; mu 10.0159 0.0271 ; a 2.9962 0.1737 ; b -6.1066 0.0755 ;
1600 -1.1981 ; mu 10.0111 -0.0141 ; a 2.9510 0.1515 ; b -6.7829 0.0769 ;
1650 -0.2561 ; mu 10.0572 0.0522 ; a 2.9078 0.1638 ; b -6.8305 0.0805 ;
1700 -0.2575 ; mu 10.0232 -0.0107 ; a 2.9649 0.1813 ; b -6.7069 0.0810 ;
1750 -0.6908 ; mu 10.0707 0.0208 ; a 3.0926 0.2406 ; b -6.7179 0.0808 ;
1800 -1.0367 ; mu 9.9810 0.0059 ; a 3.3293 0.1906 ; b -6.6517 0.0790 ;
1850 -1.6434 ; mu 9.9521 -0.0388 ; a 3.3980 0.1691 ; b -6.6495 0.0772 ;
1900 -1.5184 ; mu 9.9756 -0.0034 ; a 3.3425 0.1545 ; b -6.2799 0.0733 ;
1950 -2.0847 ; mu 10.0348 0.0282 ; a 3.6111 0.1194 ; b -6.3214 0.0722 ;
2000 -0.9142 ; mu 9.9772 0.0270 ; a 3.4761 0.1158 ; b -6.1276 0.0783 ;

混合モデルの2つのコンポーネントの平均パラメータは、だいたい$10$と$0$付近で落ち着いています。

また、提案分布のパラメータのうち、$a$と$b$のそれぞれの平均パラメータをそのまま使って、
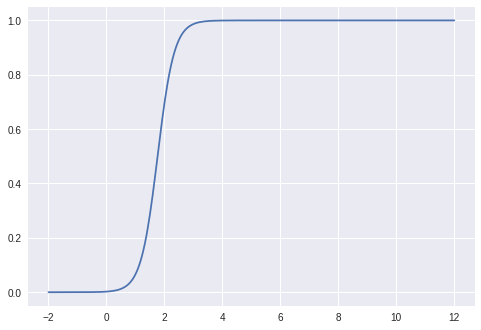
関数$\theta$のグラフを描いてみると、以下のようになりました。

import matplotlib.pyplot as plt

m_a, m_b = m_a.item(), m_b.item()
x = np.linspace(-2, 12, 301)
y = 1 / (1 + np.exp(- (m_a * x + m_b)))
plt.plot(x, y)

$0$と$10$の間に境界があればいいので大丈夫っぽいです。$0$のほうにかなり寄っているのが気になりますが・・・。

おわりに

すでに述べたように、混合正規分布についてはEMアルゴリズムでパラメータ推定ができます。
今回はあえて離散的な隠れ変数をそのまま式に残して、その値が従う分布をreparameterizeしました。
こうして問題を難しくしてから、variational optimizationで解いてみました。

前回言及したbaselineを考えなくても何とかなっているのは、解きやすい問題だったからかもしれません。

---

1. Gilles Louppe, Joeri Hermans, and Kyle Cranmer. Adversarial Variational Optimization of Non-Differentiable Simulators. https://arxiv.org/abs/1707.07113 ↩