Layer normalizationのbackpropagation

はじめに

この記事では、layer normalizationを使ったときのbackpropagationについて書いています。
原論文は[1607.06450] Layer Normalizationです。
論文にbackpropagationの式は書いてありません。
フレームワークを使えば手計算で微分する必要はないからです。

ユニットの出力

第$l$番目のレイヤにある第$i$番目のユニットに対して、
前のレイヤから入ってきた入力値に重みを掛けて足し合わせたものを$a_i^l$をとします。つまり、

a_i^l = \sum_j w_{i,j}^l h_j^l

です。通常なら、これにバイアス項$b_i^l$を足して、非線形の関数$f$を適用したものが、
このユニットからの出力$h_i^{l+1}$となります。つまり、

h_i^{l+1} = f(a_i^l + b_i^l)

です。

Layer normalization

Layer normalizationでは、レイヤごとに、$a_i^l$を以下の式によってnormalizeします。

\bar{a_i}^l = \frac{g_i^l}{\sigma^l}(a_i^l - \mu^l)

ここで、平均$\mu^l$と標準偏差$\sigma^l$は、

\begin{align}
\mu^l & = \frac{1}{H}\sum_{i=1}^H a_i^l
\\
\sigma^l & = \sqrt{\frac{1}{H}\sum_{i=1}^H(a_i^l - \mu^l)^2}
\end{align}

とレイヤごとに計算されます。$H$は、いま考えているレイヤにあるユニットの個数です。

こうしてnormalizeされた$\bar{a_i}^l$を、$a_i^l$の代わりに使います。
つまり、ユニットからの出力は$h_i^{l+1} = f(\bar{a_i}^l + b_i^l)$となります。

前向きの計算をグラフにする

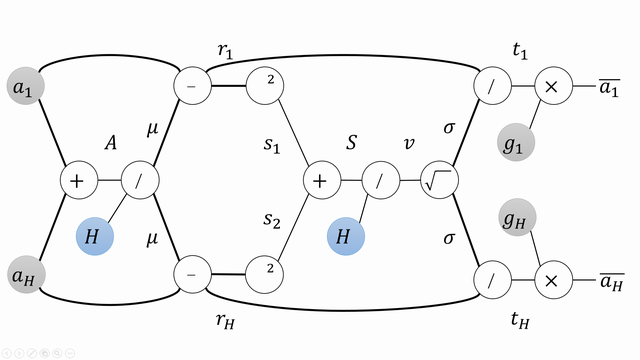
上のnormalizationの計算をグラフとして描いてみます。
$a_1$と$a_H$しか示していませんが、実際には$H$個のユニットすべてについて同様のグラフが描けます。
また、途中経過を表す変数を適当に導入しています。

この図にしたがって、前向き（図で左から右）の計算を書き下すと、以下のようになります。
何番目のレイヤかを表す上付きの$l$は省略します。

\begin{align}
A & = \sum_{i=1}^H a_i \\
\mu & = \frac{A}{H} \\
r_i & = a_i - \mu & (i=1,\ldots,H) \\
s_i & = r_i^2 & (i=1,\ldots,H) \\
S & = \sum_{i=1}^H s_i \\
v & = \frac{S}{H} \\
\sigma & = \sqrt{v} \\
t_i & = \frac{r_i}{\sigma} & (i=1,\ldots,H) \\
\bar{a_i} & = g_i t_i & (i=1,\ldots,H)
\end{align}

Layer normalizationのbackpropagation

Backpropagationでは、損失関数を$L$として、$\frac{\partial L}{\partial \bar{a_i}}$や$\frac{\partial L}{\partial b_i}$を求める必要があります。

\begin{align}
\frac{\partial L}{\partial \bar{a_i}}
& =\frac{\partial L}{\partial h_i^{l+1}}\frac{\partial h_i^{l+1}}{\partial \bar{a_i}}
=\frac{\partial L}{\partial h_i^{l+1}}f^\prime(\bar{a_i}^l + b_i^l)
\\
\frac{\partial L}{\partial b_i}
& =\frac{\partial L}{\partial h_i^{l+1}}\frac{\partial h_i^{l+1}}{\partial b_i}
=\frac{\partial L}{\partial h_i^{l+1}}f^\prime(\bar{a_i}^l + b_i^l)
\end{align}

バイアス項については、ここで求めた$\frac{\partial L}{\partial b_i}$を更新計算に使います。

では、$\frac{\partial L}{\partial \bar{a_i}}$よりも後ろのbackpropagationの計算はどうなるでしょうか。

上の図を見ながら、ひとつずつさかのぼっていきます。

\begin{align}
\frac{\partial L}{\partial g_i}
&= \frac{\partial L}{\partial \bar{a_i}}\frac{\partial \bar{a_i}}{\partial g_i}
= \frac{\partial L}{\partial \bar{a_i}}t_i
= \frac{\partial L}{\partial \bar{a_i}}\frac{\bar{a_i}}{g_i}
\\
\frac{\partial L}{\partial t_i}
&= \frac{\partial L}{\partial \bar{a_i}}\frac{\partial \bar{a_i}}{\partial t_i}
= \frac{\partial L}{\partial \bar{a_i}}g_i
\end{align}

$\sigma$については、合流点になっているので、以下のように和になります。

\begin{align}
\frac{\partial L}{\partial \sigma}
& = \sum_{i=1}^H \frac{\partial L}{\partial t_i}\frac{\partial t_i}{\partial \sigma}
= - \frac{1}{\sigma^2} \sum_{i=1}^H \frac{\partial L}{\partial t_i} r_i
= - \frac{1}{\sigma^2} \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}} g_i (a_i - \mu)
\\
& = - \frac{1}{\sigma} \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}} \bar{a_i}
\end{align}

さらにさかのぼります。

\begin{align}
\frac{\partial L}{\partial v}
& = \frac{\partial L}{\partial \sigma}\frac{\partial \sigma}{\partial v}
= \frac{\partial L}{\partial \sigma}\frac{1}{2\sqrt{v}}
= \frac{\partial L}{\partial \sigma}\frac{1}{2\sigma}
\\
\frac{\partial L}{\partial S}
& = \frac{\partial L}{\partial v}\frac{\partial v}{\partial S}
= \frac{\partial L}{\partial v}\frac{1}{H}
= \frac{\partial L}{\partial \sigma}\frac{1}{2\sigma H}
\\
\frac{\partial L}{\partial s_i}
& = \frac{\partial L}{\partial S}\frac{\partial S}{\partial s_i}
= \frac{\partial L}{\partial S} 1
= \frac{\partial L}{\partial \sigma}\frac{1}{2\sigma H}
\end{align}

$r_i$は、2つのパスの合流点になっています。

\begin{align}
\frac{\partial L}{\partial r_i}
& = \frac{\partial L}{\partial t_i}\frac{\partial t_i}{\partial r_i} + \frac{\partial L}{\partial s_i}\frac{\partial s_i}{\partial r_i}
= \frac{\partial L}{\partial t_i}\frac{1}{\sigma} + 2 \frac{\partial L}{\partial s_i}r_i
\\
& = \frac{1}{\sigma} \Big( \frac{\partial L}{\partial \bar{a_i}} g_i
+ \frac{\partial L}{\partial \sigma}\frac{a_i - \mu}{H} \Big)
\end{align}

$\mu$は合流点になっています。また、次のように計算結果を簡単にできます。

\begin{align}
\frac{\partial L}{\partial \mu}
& = \sum_{i=1}^H \frac{\partial L}{\partial r_i}\frac{\partial r_i}{\partial \mu}
= - \sum_{i=1}^H \frac{\partial L}{\partial r_i}
= - \frac{1}{\sigma} \sum_{i=1}^H \Big( \frac{\partial L}{\partial \bar{a_i}} g_i
+ \frac{\partial L}{\partial \sigma}\frac{a_i - \mu}{H} \Big)
\notag \\
& =
- \frac{1}{\sigma} \bigg( \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}} g_i
+ \frac{\partial L}{\partial \sigma}\frac{\sum_{i=1}^H (a_i - \mu)}{H} \bigg)
\\
& =
- \frac{1}{\sigma} \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}} g_i
\end{align}

さらにさかのぼります。

\begin{align}
\frac{\partial L}{\partial A}
= \frac{\partial L}{\partial \mu}\frac{\partial \mu}{\partial A}
= \frac{\partial L}{\partial \mu}\frac{1}{H}
= - \frac{1}{\sigma H} \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}} g_i
\end{align}

$a_i$は、2つのパスの合流点になっています。

\begin{align}
\frac{\partial L}{\partial a_i}
& = \frac{\partial L}{\partial r_i}\frac{\partial r_i}{\partial a_i}
+ \frac{\partial L}{\partial A}\frac{\partial A}{\partial a_i}
= \frac{\partial L}{\partial r_i} 1 + \frac{\partial L}{\partial A} 1
\notag \\
& = \frac{1}{\sigma} \bigg( \frac{\partial L}{\partial \bar{a_i}} g_i
+ \frac{\partial L}{\partial \sigma}\frac{a_i - \mu}{H} \bigg)
- \frac{1}{\sigma H} \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}} g_i
\notag \\
& = \frac{1}{\sigma} \bigg\{ \bigg( \frac{\partial L}{\partial \bar{a_i}} g_i
- \frac{1}{H} \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}} g_i \bigg)
- \frac{a_i - \mu}{\sigma}
\frac{1}{H} \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}}\bar{a_i} \bigg\}
\notag \\
& = \frac{1}{\sigma} \bigg\{ \bigg( \frac{\partial L}{\partial \bar{a_i}} g_i
- \frac{1}{H} \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}} g_i \bigg)
- \frac{\bar{a_i}}{g_i} \bigg(
\frac{1}{H} \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}}\bar{a_i} \bigg) \bigg\}
\end{align}

まとめ

実際の計算に必要なものだけをまとめます。

\begin{align}
\frac{\partial L}{\partial g_i}
& = \frac{\partial L}{\partial \bar{a_i}}\frac{\bar{a_i}}{g_i}
\\
\frac{\partial L}{\partial a_i}
& = \frac{1}{\sigma} \bigg\{ \bigg( \frac{\partial L}{\partial \bar{a_i}} g_i
- \frac{1}{H} \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}} g_i \bigg)
- \frac{\bar{a_i}}{g_i} \bigg(
\frac{1}{H} \sum_{i=1}^H \frac{\partial L}{\partial \bar{a_i}}\bar{a_i} \bigg) \bigg\}
\end{align}

各レイヤについて$\sigma$は前向き計算のときに保存しておく必要がありそうです。
ここで求めた$\frac{\partial L}{\partial g_i}$は$g_i$の更新に使います。

最初のほうで書いたように、$a_i^l = \sum_j w_{i,j}^l h_j^l$でしたので、

\begin{align}
\frac{\partial L}{\partial w_{i,j}^l}
& = \frac{\partial L}{\partial a_i^l}\frac{\partial a_i^l}{\partial w_{i,j}^l}
= \frac{\partial L}{\partial a_i^l} h_j^l
\\
\frac{\partial L}{\partial h_j^l}
& = \sum_{i=1}^H \frac{\partial L}{\partial a_i^l}\frac{\partial a_i^l}{\partial h_j^l}
= \sum_{i=1}^H \frac{\partial L}{\partial a_i^l} w_{i,j}^l
\end{align}

となります。$\frac{\partial L}{\partial w_{i,j}^l}$は重み$w_{i,j}^l$の更新に使います。
$\frac{\partial L}{\partial h_j^l}$については、さらに下のレイヤについて、上のような計算を続けます。

---

注：こんなふうにいちいち演算子ごとに計算を分割して微分の計算をしていく必要はありませんが、
一種の計算練習としてこれを書きました。