ニューラルネットで解像度に依存しない画像表現(MNIST編)

はじめに

ニューラルネットで画像を出力する際、通常は解像度ごとに専用のモデルを用意して学習を行うことになります。
今回は解像度に依存しない形で、画像上の任意の点からサンプリングを行うモデルについて考えてみます。
画像上の点$ (u, v) $の値を$ P_{u, v} $とすると、
$$ P_{u, v} = f(u, v, z_1, ..., z_n) $$
となる関数$ f $をニューラルネットで表現したいわけです。ここで、$ \lbrace z_1, ..., z_n \rbrace $は画像を表す潜在表現です。
今回はこの潜在表現をVAEのエンコーダ部を用いて得ることにして、デコーダ部となる関数$ f $を4層の全結合ニューラルネットで表現してみました。

Chainerによる実装(github)

実装

全体の構成は通常のVAEと同じです。
違いはデコーダ部で、こうなっています。

model.py

class SamplingDecoder(chainer.Chain):
    def __init__(self, input_size):
        super().__init__()
        units = [2 + input_size, 256, 256, 256, 1]
        initializer = chainer.initializers.HeNormal()
        with self.init_scope():
            self.linear1 = chainer.links.Linear(units[0], units[1], initialW=initializer)
            self.linear2 = chainer.links.Linear(units[1], units[2], initialW=initializer)
            self.linear3 = chainer.links.Linear(units[2], units[3], initialW=initializer)
            self.linear4 = chainer.links.Linear(units[3], units[4], initialW=initializer)

    def decode(self, z):
        h = z
        h = self.linear1(h)
        h = chainer.functions.relu(h)
        h = self.linear2(h)
        h = chainer.functions.relu(h)
        h = self.linear3(h)
        h = chainer.functions.relu(h)
        h = self.linear4(h)
        return h

    def __call__(self, z, x0_shape):
        xp = self.xp

        # Generate (u, v) coordinates for every samples.
        u = xp.linspace(-1.0, 1.0, x0_shape[2], dtype=xp.float32)
        v = xp.linspace(-1.0, 1.0, x0_shape[3], dtype=xp.float32)
        uv = xp.broadcast_arrays(u[None, None, :, None], v[None, None, None, :])
        uv = xp.concatenate(uv, 1)
        uv = xp.broadcast_to(uv, (z.shape[0], uv.shape[1], uv.shape[2], uv.shape[3]))

        z = z[:, :, None, None]
        z = chainer.functions.broadcast_to(z, (z.shape[0], z.shape[1], uv.shape[2], uv.shape[3]))

        # Combine them.
        uvz = chainer.functions.concat((uv, z))
        uvz = chainer.functions.transpose(uvz, (0, 2, 3, 1))
        uvz = chainer.functions.reshape(uvz, (-1, uvz.shape[3]))

        y = self.decode(uvz)

        y = chainer.functions.reshape(y, (x0_shape[0], x0_shape[2], x0_shape[3], x0_shape[1]))
        y = chainer.functions.transpose(y, (0, 3, 1, 2))
        return y

まず、画像上で出力値を得たい全ての点について座標値(u, v)を生成しています。これを潜在表現$ \lbrace z_1, ..., z_n \rbrace $とあわせてdecode()に与えるわけです。
出力に対する損失関数としては、ベルヌーイ分布の負の対数尤度を用います。

出力

潜在表現を8次元とした学習結果です。

1エポック目

(上:元データ、下:学習後のモデルによる168x168でのレンダリング結果)

50エポック目

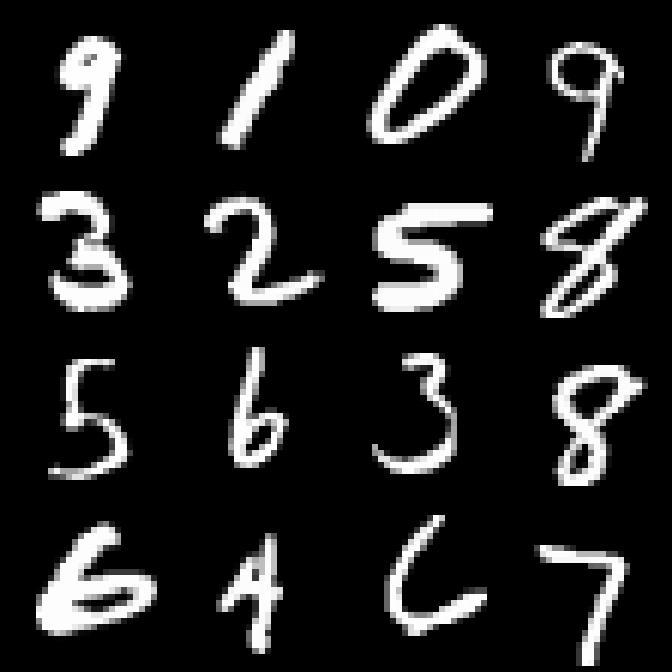
(上:元データ、下:学習後のモデルによる168x168でのレンダリング結果)

うまくデータを再現できているようです。
ただし、通常の画像補間アルゴリズムによる結果と大して変わらないような気もします。