マニピュレーターのエンドポイントから関節角度を推定する逆運動学．
今回は，FABRIK(Forward And Backward Reaching Inverse Kinematics,[著]Anrdreas Aristidou)と呼ばれる逆運動学アルゴリズムを用いて逆運動学解を導出します．
使用言語はPythonです．
文献，著者HP，解説(ROBLOX)

今回の目的

FABRIKアルゴリズムを用いて各関節の座標を求めるプログラムの作成
（制約のない状況なので，あらゆる関節角度をとる）

プログラム

逆運動学解を導出するために必要なプログラムを準備します.
- Initialized.py (リンク構造の初期状態）
- forward_and_backward.py（計算をするプログラム)

forward_and_backward.py

エンドポイントからベースポジションへ戻る方向をbackward
ベースポジションからエンドポイントへ進む方向をforward　とします（ややこしい！）
以下の図がプログラムの流れを図示したものです．

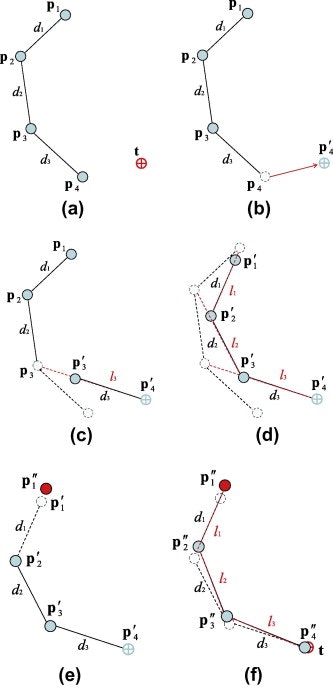
(a). ターゲットポジションを設定する．
(b). ターゲットポジションにエンドポイントを置き，新規エンドポイントとする．
(c). 新規ポジションi+1番目とポジションi番目との直線上にリンクの長さを合わせた場所をi番目の新規ポジションとする．
(d). ベースポジションまで計算をする．(このとき．新規ベースポジションと本来のベースポジションがズレていることが確認でき，逆方向への計算が必要となる)
(e). 基のベースポジションを新規ベースポジションとする．
(f). 求めた新規ポジションに対し，逆方向から計算する．
文献:Fig.3

この流れをターゲットポジションとエンドポイントのズレが許容範囲内に収まるまでa~fを繰り返します．
a~dまでをbackward関数，e,fをforward関数にて計算します．
ターゲットポジションがリンクの到達可能域にない場合を含め，全体の流れをsolve関数にて計算します．

import

import numpy as np
import math

計算のためにnumpyとmathをインポートしておきます

init

    def __init__(self, positions, target, linklength):
        self.P = positions
        self.t = target
        self.b = self.P[0]
        self.L = linklength
        self.n = len(self.L) 

        self.tol = tolerance

self.P（配列）　各ジョイントポジション配列
self.t（変数）　ターゲットポジション
self.b（変数）　ベースポジション
self.L（配列）　各リンクの長さ配列
self.n（変数）　リンクの配列長
self.tol（変数）　ターゲットポジションとエンドポイントの誤差の許容値

以上の値を初期化します．

backward関数

backward関数ではエンドポイントからベースポジション方向へ新規ジョイントを決定します．

ターゲットポジションを新規エンドポイントとしてセット
新規ジョイントi+1番目とジョイントi番目の距離を出す
リンクの距離と2.で出した距離の商を取る
3.の結果とジョイントi番目の積，自然数1と3.の結果の差を取り新規ジョイントi+1番目との積を求め，合計値を新規ジョイントi番目とする

このようにして，backward方向での新規ジョイントが導出されます．
新規ベースポジションは，基のベースポジションと位置がズレるため，forward方向へ計算する必要があります．

    def backward(self):
        self.P[n] = self.t

        for j in range(self.n):
            i = (self.n-1)-j
            line = abs(np.linalg.norm(self.P[i+1] - self.P[i]))
            div = self.L[i] / line
            pos = (1-div) * self.P[i+1] + div * self.P[i]
            self.P[i] = pos

forward関数

forward関数ではベースポジションからエンドポイント方向へ新規ジョイントを決定します．

ベースポジションを新規ベースポジションとしてセット
新規ジョイントi番目とジョイントi+1番目の距離を出す
リンクの距離と2.で出した距離の商を取る
3.の結果とジョイントi+1番目の積，自然数1と3.の結果の差を取り新規ジョイントi番目との積を求め，合計値を新規ジョイントi+1番目とする

このようにしてforward方向の新規ジョイントが導出されます．

    def forward(self):
        self.P[0] = self.b

        for i in range(self.n):
            line = abs(np.linalg.norm(self.P[i+1] - self.P[i]))
            div = self.L[i] / line
            pos = (1-div) * self.P[i] + div * self.P[i+1]
            self.P[i+1] = pos

solve関数

solve関数ではbackward関数とforward関数を用いて全体的なFABRIKアルゴリズムを一連の流れで計算します．
ターゲットポジションが到達可能域外であれば，ベースポジションからターゲットポジションの直線上に到達可能な距離までのリンク構造を返します．
ターゲットポジションが到達可能域内であれば，backward関数，forward関数を用いてターゲットポジションとエンドポイントの誤差が許容範囲内に収まるまで計算を繰り返します．10回繰り返しても許容範囲を超える場合はbreakします．

    def solve(self):
        if abs(np.linalg,norm(self.t - self.P[0])) > sum(self.L):
            # target is out of reach
            for i in range(self.n):
                line = abs(np.linalg.norm(self.t - self.P[i]))
                div = self.L[i] / line
                self.P[i+1] = (1-div) * self.P[i] + div * self.t

        else:
            # target is in reach
            bcount = 0
            dif = abs(np.linalg.norm(self.P[self.n] - self.t))
            while dif > self.tol:
                self.backward()
                self.forward()
                dif = abs(np.linalg.norm(self.P[self.n] - self.t))

                bcount+=1
                if bcount > 10:
                    break

参考文献

ロボット工学（改訂版）ー機械システムのベクトル解析ー

逆運動学解を導出するFABRIKアルゴリズムをPythonで実装する