参考元
平方根を使わずに距離を求める
平方根を使わずに高速で2点間の距離を近似する
距離を求めるときには平方根を用いますが、平方根の計算はコストが高いため、FPUをもっていないマイコンやFPGAではできることであれば平方根を使用せずに距離を求めたいという場面があると思います。
高い精度が必要でない場合、下記のような近似計算で十分です。
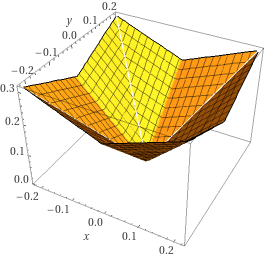
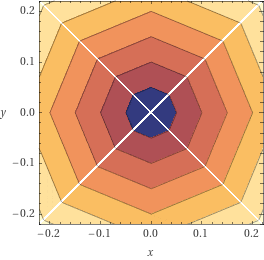
正8角形で近似する場合
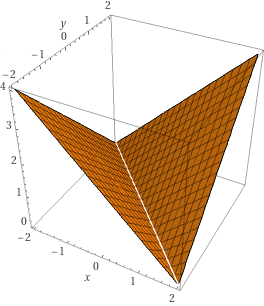
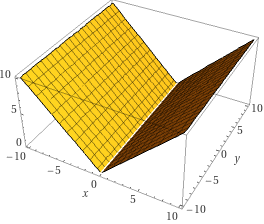
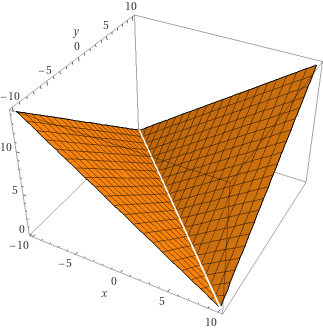
z=max(x,y)-min(x,y)
という式は3次元的に谷のような形です。
この谷状の式を方向を-45度、0度、45度、90度のものを足し係数を調整することで
となります。
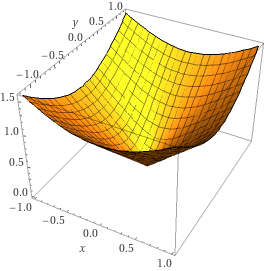
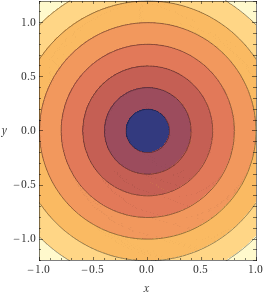
これは距離を求める次式の
z=\sqrt{x^2+y^2}
の近似になっています。
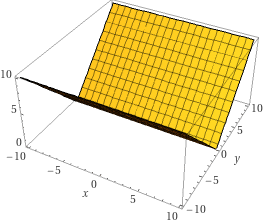
0度の谷状の式は次式で
\begin{align}
z=max(0,y)-min(0,y)
\end{align}
90度の谷状の式は次式で
\begin{align}
z=max(x,0)-min(x,0)
\end{align}
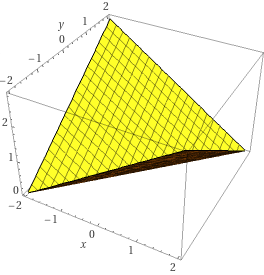
45度の谷状の式は次式で
\begin{align}
z=max(\frac 1 {\sqrt 2} x,\frac 1 {\sqrt 2} y)-min(\frac 1 {\sqrt 2} x,\frac 1 {\sqrt 2} y)
\end{align}
-45度の谷状の式は次式で
\begin{align}
z=max(\frac 1 {\sqrt 2} x,-\frac 1 {\sqrt 2} y)-min(\frac 1 {\sqrt 2} x,-\frac 1 {\sqrt 2} y)
\end{align}
となります。
それぞれの谷状の式を重ね合わせ(足し算)ると次式となります。
\begin{align}
z=\sqrt{x^2+y^2} \approx & C\Biggl(max(x,0)-min(x,0) \\
& +max(0,y)-min(0,y) \\
&+max(\frac 1 {\sqrt 2} x,\frac 1 {\sqrt 2} y)-min(\frac 1 {\sqrt 2} x,\frac 1 {\sqrt 2} y) \\
&+max(\frac 1 {\sqrt 2} x,-\frac 1 {\sqrt 2} y)-min(\frac 1 {\sqrt 2} x,-\frac 1 {\sqrt 2} y) \Biggr)\\
\end{align}
この時、Cは調整係数です。
\begin{align}
x=1,y=0
\end{align}
のとき、距離は1であるべきなので、
\begin{align}
1= & C\Biggl(max(1,0)-min(1,0) \\
& +max(0,0)-min(0,0) \\
&+max(\frac 1 {\sqrt 2} 1,\frac 1 {\sqrt 2} 0)-min(\frac 1 {\sqrt 2} 1,\frac 1 {\sqrt 2} 0) \\
&+max(\frac 1 {\sqrt 2} 1,-\frac 1 {\sqrt 2} 0)-min(\frac 1 {\sqrt 2} 1,-\frac 1 {\sqrt 2} 0) \Biggr)\\
\end{align}
そして、
\begin{align}
1= & C\Biggl(1-0 +0+0 + \frac 1{\sqrt 2} - 0 +\frac 1 {\sqrt 2} - 0 \Biggr)
\end{align}
\begin{align}
C= \sqrt 2 -1
\end{align}
これで係数Cが求まりました。
範囲を
x>0,y>0
で考えて式変形すると
\begin{align}
z=\sqrt{x^2+y^2} \approx & C\Biggl(x \\
& +y \\
&+\frac 1 {\sqrt 2}(max( x,y)-min( x, y)) \\
&+\frac 1 {\sqrt 2}( x+y) \Biggr)\\
\end{align}
そして、
\begin{align}
z=\sqrt{x^2+y^2} \approx & C\Biggl(\Bigl(1+\frac 1 {\sqrt 2}\Bigr)(x+y) \\
&+\frac 1 {\sqrt 2}(max( x,y)-min( x, y)) \Biggr)\\
\end{align}
ここで、
\begin{align}
x+y=max(x,y)+min(x,y)
\end{align}
とも記述できるため、
\begin{align}
z=\sqrt{x^2+y^2} \approx & C\Biggl(\Bigl(1+\frac 1 {\sqrt 2}\Bigr)(max(x,y)+min(x,y)) \\
&+\frac 1 {\sqrt 2}(max( x,y)-min( x, y)) \Biggr)\\
\end{align}
となり、
\begin{align}
z=\sqrt{x^2+y^2} \approx(max(x,y)+(\sqrt2-1)min(x,y))
\end{align}
しかし、このままでは、最小の誤差は0%であるものの(0°、45°、90°の線上)、最大の誤差(pi/8=22.5°、67.5°の線上)となるときの近似計算の結果および誤差は、
\begin{align}
& Distance_{max}=\frac 1 {cos\Bigl(\frac {\pi}{8}\Bigr)}=1.08239...\\
& E_{max}=Distance_{max}-1=8.239... \%
\end{align}
となり、正負の正のみに偏って誤差があることになります。
最大誤差 E_max と最小誤差 E_min をそれぞれ小さくしたいのですが、これには最小二乗などさまざまな考え方があります。
今回は単純に
\lvert E_{max} \rvert=\lvert E_{min} \rvert
となるように調整することとします。
最大誤差となるときの近似計算の値をもとに補正をかけると、補正係数は、
\begin{align}
C_{err}&=\frac {2}{Distance_{max}+1}\\
&=\frac {2}{\frac 1 {cos\Bigl(\frac {\pi}{8}\Bigr)}+1}\\
&=\frac{2\cos(\frac {\pi} 8)}{1+\cos(\frac {\pi} 8)}
\end{align}
になります。よって近似計算式は
\begin{align}
z=\sqrt{x^2+y^2} \approx \frac{2\cos(\frac {\pi} 8)}{1+\cos(\frac {\pi} 8)}(max(x,y)+(\sqrt2-1)min(x,y))
\end{align}
となります。
範囲を
-\infty<x<\infty,-\infty<y<\infty
に広げるために絶対値をとって、
\begin{align}
z=\sqrt{x^2+y^2} \approx \frac{2\cos(\frac {\pi} 8)}{1+\cos(\frac {\pi} 8)}(max(\lvert x \rvert,\lvert y \rvert)+(\sqrt2-1)min(\lvert x \rvert,\lvert y \rvert))
\end{align}
となります。
このとき、最大最小誤差は
\begin{align}
E&=\pm Distance_{max} C_{err}-1\\
&=\pm \frac 1 {cos\Bigl(\frac {\pi}{8}\Bigr)} \frac{2\cos(\frac {\pi} 8)}{1+\cos(\frac {\pi} 8)}-1\\
&=\pm \frac{1-\cos(\frac {\pi} 8)}{1+\cos(\frac {\pi} 8)}\\
&=\pm\tan ^2 \Bigl(\frac {\pi} {16}\Bigr)=\pm3.9566...\%
\end{align}
となります。
整数計算の場合には、
\begin{align}
\frac{1024}{1024}\frac{2\cos(\frac {\pi} 8)}{1+\cos(\frac {\pi} 8)}&= \frac{983.484...}{1024},\\ \frac{1024}{1024}\frac{2\cos(\frac {\pi} 8)}{1+\cos(\frac {\pi} 8)}(\sqrt2-1)&= \frac{407.373...}{1024}
\end{align}
ですので、
\begin{align}
z=\sqrt{x^2+y^2} \approx \frac {983}{1024} max(\lvert x \rvert,\lvert y \rvert)+\frac {407}{1024}min(\lvert x \rvert,\lvert y \rvert))
\end{align}
となります。
ところで、この係数は参考元の武内氏のパラメータ最適化の結果 (983, 407) と同様になりました。
平方根を使わずに距離を求める
Cのコードでは
#include <stdio.h>
#include <stdlib.h>
#define MIN(i, j) (((i) < (j)) ? (i) : (j))
#define MAX(i, j) (((i) > (j)) ? (i) : (j))
int distance(int x, int y) {
x = abs(x);
y = abs(y);
return (MAX(x, y) * 983 + MIN(x, y) * 407) >> 10;
}
int main() {
printf("1000, 1000 : %d\n", distance(1000, 1000));
return 0;
}
となります。
正24角形で近似する場合
正8角形での方法は正n角形でも同じように適用できます。
正24角形で近似する場合は同様に-75°,-60°,-45°,-30°,-15°,0°,15°,30°,45°,60°,75°,90°の谷の式を重ね合わせ(足し算)し、X=1,Y=0のときに距離が1となることを利用し未定の係数を求め、その後、誤差を補正します。
そうして求まった近似計算式は次式となります。
\begin{align}
\sqrt{x^2+y^2} \approx &C_0\Bigl(C_1 (\lvert x \rvert+\lvert y \rvert)+f(\frac 1 {\sqrt2}\lvert x \rvert, \frac 1 {\sqrt2}\lvert y \rvert)+\\
&f(\frac {\sqrt3+1} {2\sqrt2}\lvert x \rvert, \frac {\sqrt3-1} {2\sqrt2}\lvert y \rvert)+
f(\frac {\sqrt3-1} {2\sqrt2}\lvert x \rvert, \frac {\sqrt3+1} {2\sqrt2}\lvert y \rvert)+\\
&f(\frac {\sqrt3} {2}\lvert x \rvert, \frac {1} {2}\lvert y \rvert)+
f(\frac {1} {2}\lvert x \rvert, \frac {\sqrt 3} {2}\lvert y \rvert)
\Bigr)
\end{align}
このとき、最大最小誤差は
\begin{align}
E=\pm\tan ^2 \Bigl(\frac {\pi} {48}\Bigr)=\pm0.4296\%
\end{align}
です。
このとき
\begin{align}
C_0&=\frac{2\cos(\frac{\pi}{24})}{1+\cos(\frac{\pi}{24})}\cdot\frac{1}{2+\sqrt2+\sqrt3+\sqrt{2\cdot3}}\\
C_1&=\frac{3+\sqrt2+\sqrt3+\sqrt{2\cdot3}}{2}\\
f(a,b)&=max(a,b)-min(a,b)
\end{align}
整数計算の場合、
#include <stdio.h>
#include <stdlib.h>
#define F(i, j) (((i) > (j)) ? ((i) - (j)) : ((j) - (i)))
int distance(int x, int y) {
int x0, y0, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6;
x0 = abs(x);
y0 = abs(y);
x3 = 4149 * x0;
y3 = 1112 * y0;
x4 = 1112 * x0;
y4 = 4149 * y0;
x5 = 3720 * x0;
y5 = 2148 * y0;
x6 = 2148 * x0;
y6 = 3720 * y0;
return ((x0 + y0) * 18461 + F(x0, y0) * 3037 + F(x3, y3) + F(x4, y4) + F(x5, y5) + F(x6, y6)) >> 15;
}
int main() {
printf("1000, 1000 : %d\n", distance(1000, 1000));
return 0;
}
正4n角形で近似する場合
例えば正32角形の場合、
\begin{align}
4n&=32\\
n&=8
\end{align}
となります。
近似計算式は次式となります。
\begin{align}
\sqrt{x^2+y^2} \approx & C_2\Biggl(C_3 (\lvert x \rvert+\lvert y \rvert)+\sum_{k=1}^{n-1}f\Biggl(\sin\Bigl(\frac{\pi k} {2 n}\Bigr)\lvert x \rvert, \cos \Bigl(\frac{\pi k} {2 n}\Bigr)\lvert y \rvert\Biggr)\Biggr)
\end{align}
ここで
\begin{align}
C_2&=\frac{2\cos(\frac{\pi}{4n})}{1+\cos(\frac{\pi}{4n})}\cdot \frac{1}{2C_3-1}\\
C_3&=1+\sum_{k=1}^{n-1}\sin\Bigl(\frac{\pi k} {2 n}\Bigr)
\end{align}
です。
このとき、最大最小誤差は
\begin{align}
E=\pm\tan ^2 \Bigl(\frac {\pi} {8n}\Bigr)
\end{align}
となります。
整数で計算するために正8角形では2^10=1024, 正24角形では2^15=32768を乗して固定小数点計算のような計算をしていますので、大きな値を入力した場合は整数型の範囲に収まらず、計算結果が合わなくなることがあります。