前回に引き続き、rustの練習を兼ねて、アルゴリズムクイックリファレンスを実装していきたいと思います。
今回は、バブルソートとマージソートを実装していきたいと思います。
インストール
こちらを参照して、rust環境を整えてください。
環境
- MacBook Pro (Sierra 10.12.6 Retina)
- 2.3GHz IntelCore i7
- Memory 16GB
- NVIDIA GeForce GT 750M 2048MB Intel Iris Pro 1536MB
- rustc v.1.19.0
バブルソート
wikipediaより。
バブルソート (bubble sort) は、ソートのアルゴリズムの一つ。隣り合う要素の大小を比較しながら整列させること。
最悪計算時間がO(n2)と遅いが、アルゴリズムが単純で実装が容易なため、また並列処理との親和性が高いことから、しばしば用いられる。
安定な内部ソート。基本交換法、隣接交換法ともいう。(単に交換法と言う場合もある)
以下、実装になります。
// バブルソート..
pub fn sort<T: Ord>(data: &mut Vec<T>) {
let len = data.len();
let mut end = len;
while end > 0 {
for i in 0..data.len() - 1 {
// 隣同士の要素を比較&入れ替え.
if data[i] > data[i + 1] { data.swap(i, i+ 1); }
}
end -= 1;
}
}
マージソート
wikipediaより。
マージソートは、ソートのアルゴリズムで、既に整列してある複数個の列を1個の列にマージする際に、小さいものから先に新しい列に並べれば、新しい列も整列されている、というボトムアップの分割統治法による。
大きい列を多数の列に分割し、そのそれぞれをマージする作業は並列化できる。
n個のデータを含む配列をソートする場合、最悪計算量O(n log n)である。分割と統合の実装にもよるが、一般に安定なソートを実装できる。
インプレースな(すなわち入力領域を出力にも使うので追加領域を必要としない)ソートも提案されているが、そうでない通常の場合は、O(n)の外部記憶を必要とする。
(ナイーブな)クイックソートと比べると、最悪計算量は少ない。ランダムなデータでは通常、クイックソートのほうが速い。
以下、実装になります。
use std::fmt::Debug;
// マージソート本体.
pub fn sort<T: Ord+Clone+Debug>(data: &mut Vec<T>) {
let mut src = data.clone();
let end = data.len();
merge_sort(&mut src, data, 0, end);
}
// マージソート実処理部.
fn merge_sort<T: Ord+Clone+Debug>(work: &mut Vec<T>, result: &mut Vec<T>, start: usize, end: usize) {
// 要素数が1つになればリターン.
if end - start < 2 { return; }
// 要素が2つしか存在しない場合、入れ替える.
if end - start == 2 {
if result[start + 1] < result[start] {
result.swap(start, start + 1);
return;
}
}
// 領域を半分に分割し、其々をソート.
let mid = (start + end) / 2;
merge_sort(result, work, start, mid);
merge_sort(result, work, mid, end);
let mut idx = start;
let mut left = start;
let mut right = mid;
while idx < end {
// 右の要素のほうが大きい、もしくは左側に要素が無い場合、右側から取得.
if left >= mid || (right < end && work[left] > work[right]) {
result[idx] = work[right].clone();
right += 1;
}
else {
result[idx] = work[left].clone();
left += 1;
}
idx += 1;
}
}
処理速度
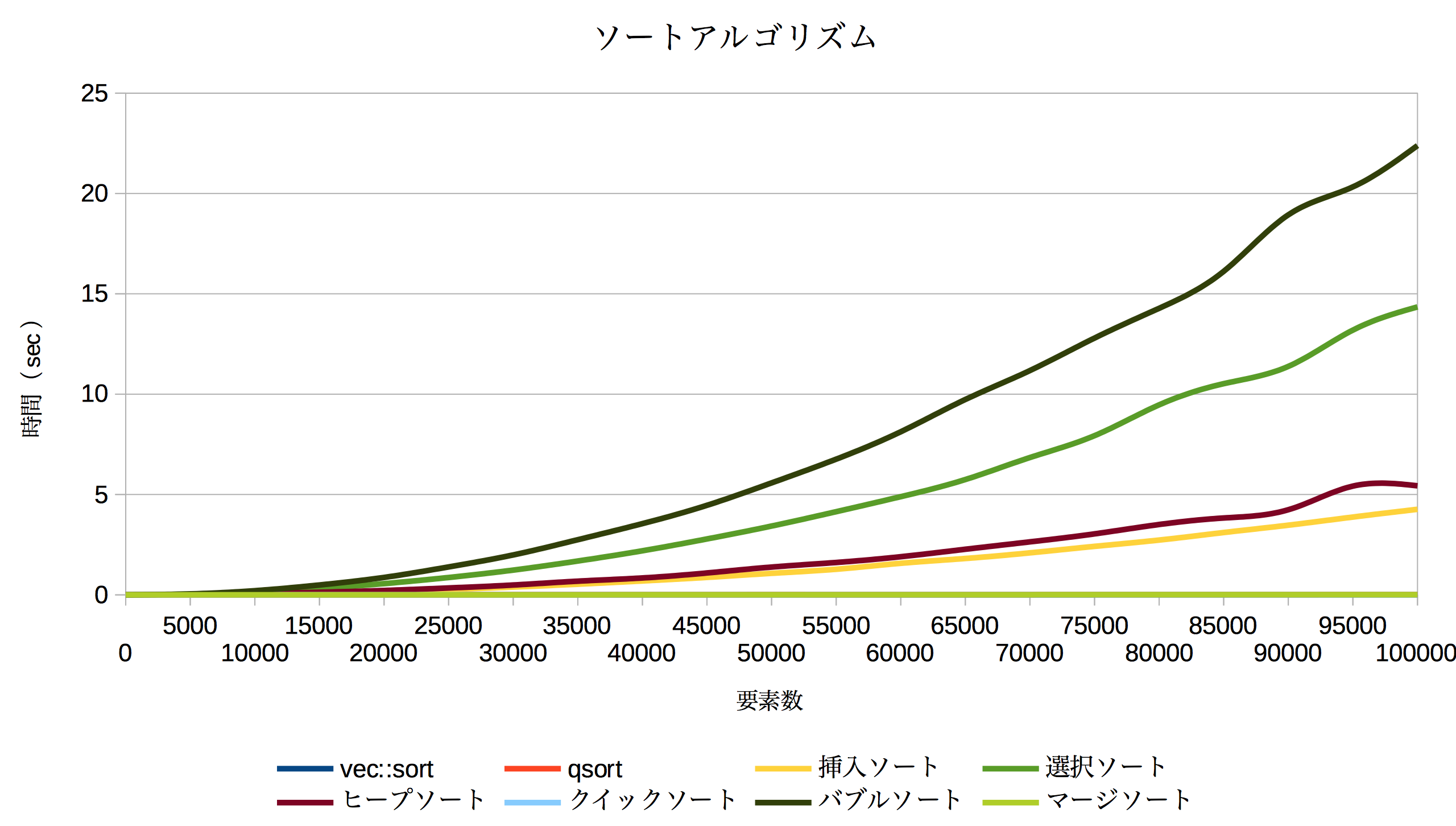
前回までの結果に今回実装したバブルソート、マージソートの処理時間を追加しました(要素数10,000)。
| ソート種別 | 処理時間 |
|---|---|
| Vec::sort | 0.000456419sec |
| 挿入 | 0.049269012sec |
| 選択 | 0.161756264sec |
| ヒープ | 0.057409270sec |
| クイック | 0.000540712sec |
| バブル | 0.207203747sec |
| マージ | 0.000770333sec |
また、要素数を増加させながら、各ソートアルゴリズムの処理時間を計測しました。
(5,000要素スタートで、5,000要素毎増加させ、100,000まで増加させた際の処理時間を計測)
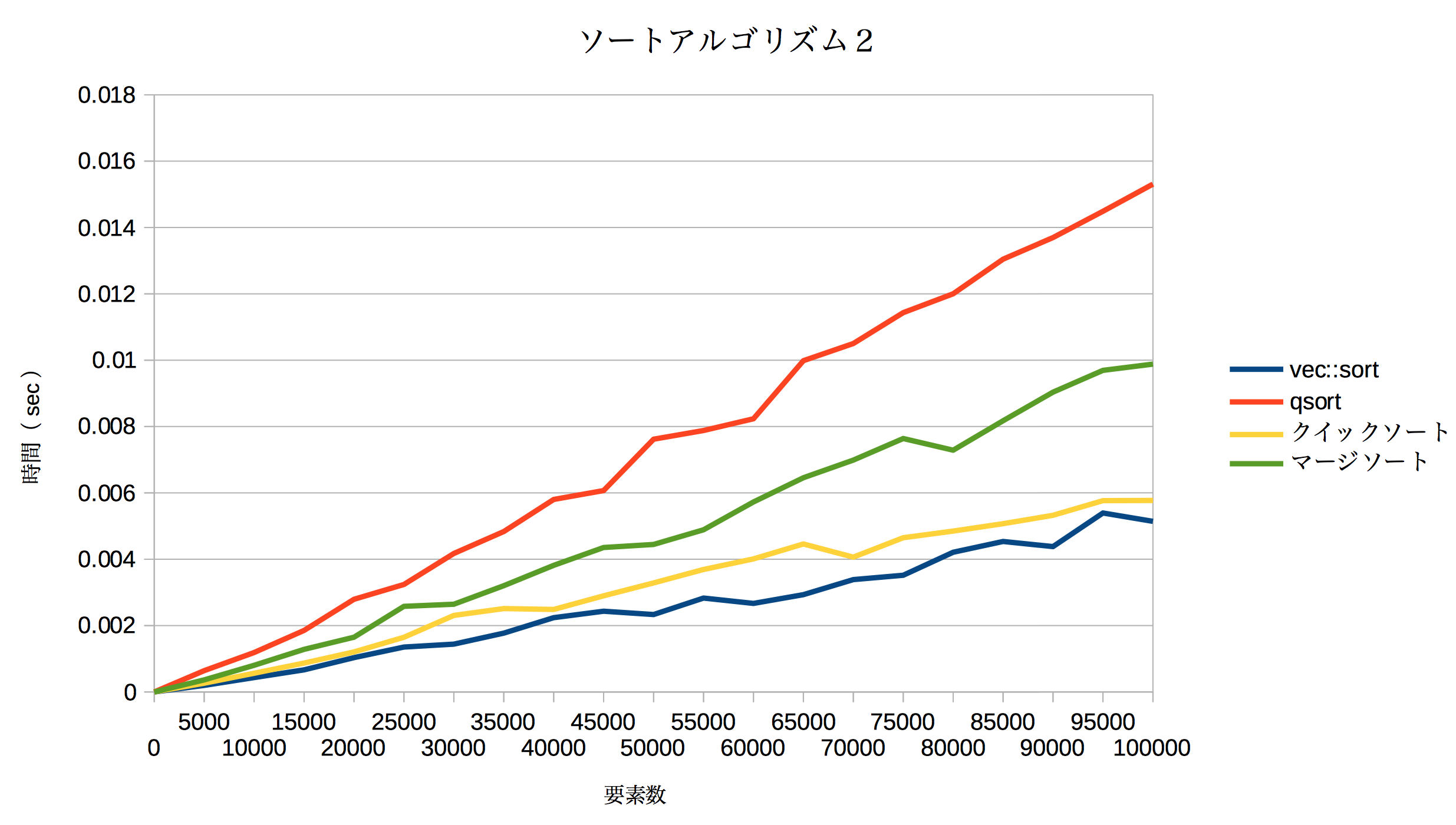
高速に動作しているソートアルゴリズムが見えにくい(というか、全く見えない)ので、別グラフで表示します。
まとめ
今まで実装した6種類のソートアルゴリズム(挿入、選択、ヒープ、クイック、バブル、マージ)に関して、まとめたいと思います。
| ソート種別 | 計算量 | メモリ使用量 | 安定性 |
|---|---|---|---|
| 選択ソート | $O(n^{2})$ | $O(1)$ | ☓1 |
| 挿入ソート | $O(n^{2})$ | $O(1)$ | ◯ |
| バブルソート | $O(n^{2})$ | $O(1)$ | ◯ |
| ヒープソート | $O(n \log n)$ | $O(1)$ | ☓ |
| クイックソート | $O(n \log n)$ | $O(\log n)$ | ☓ |
| マージソート | $O(n \log n)$ | $O(n)$2 | ◯ |
計算量の評価(O-記法)
計算量は、$O(f(n))$として表現されます(O-記法)。
nを無限大にまで増加した場合(つまり、nが非常に大きくなった場合)、計算量がどのように変化するのかを示したものです。
代表的なものに関して、例を上げてみます。
| O-記法 | 概要 | 例 |
|---|---|---|
| $O(1)$ | 定数時間で処理が完了する。データ数に依存しない。 | 配列から1つのデータを取り出す |
| $O(N)$ | データ数に比例。ループを一回だけ行っているものが該当。 | 線形探索(配列から1つのデータを探索) |
| $O(N^{2})$ | データの自乗に比例。二重のループ処理を行っているものが該当。 | 挿入ソート、バブルソート |
| $O(\log N)$ | データ数の対数に比例。処理を行う度に対象とするデータ数が減る。 | バイナリサーチ |
| $O(N!)$ | データ数の階乗に比例。 | 巡回セールスマン問題 |
ソートの安定性とは?
「安定なソート」とは、キーが同じである要素が2つ以上存在するデータをソートした場合、ソート前後で順番が変化しないものを指します。
例えば、クイックソートやヒープソートでは、順番が変わる可能性があるので「不安定なソート」、挿入ソートやマージソートでは順番が変わらない為、「安定なソート」となります。
参考
- ランダウの記号
- 計算量オーダーについて
-
Algorithm Visualizer
- アルゴリズムをVisual化するサービス。色々なアルゴリズムをVisual化できる。