Deep Learningを使った強化学習(DQN)を覚える必要が生じたので、必要な部分絞って勉強し直してみました。
理解度のスタートラインは、古典的な強化学習の概念を知っているレベルです。
強化学習について
強化学習は機械学習のカテゴリで言えば「教師なし学習」に類します。教師あり学習のように初めから答えが定義されているわけではなく、強化学習はある地点の状態において与えられた「行動の選択肢」からその行動の結果得られる「報酬」によって学習していきます。
この「報酬」が最大になるよう行動をすればよいというわけですが、「報酬」は行動ごとに与えられるのではなく、「連続した行動」に対して与えられます。そのため連続した行動の結果得られる「報酬」から、その地点での評価を更新していきます。
昔バレーボールをやっていたのでこれに例えると、得点することが報酬として設定できますが、この得点に至るまでの行動(レシーブする、トスをする、アタックを打つ、サーブを打つ)それ自体には報酬が与えられません。ボールが地面に落ちて、はじめて一連の行動が良かったのか悪かったのか判明します。このようにしてそれぞれ行動の評価を更新していきます。こうして得点するための最適な行動を学習していきます。
まだまだ抽象的な説明にしかならないので、強化学習をモデル化して考えていきます。
マルコフ決定過程(MDP)
強化学習で学習させたい問題を、マルコフ決定過程(Markov Decision Process, MDP)の問題としてモデル化します。
各要素を以下のように定義します。
- Agent
- 行動を学習していく行動主体となります。バレーボールで言えば選手に相当する部分。
- Action; $a$
- 行動を表します。
- Status; $s$
- 状態を表します。ゲームで言えば特定の局面となります。
- Reward; $r$
- Actionの結果、得られる報酬を表します。
- Policy; $\pi$
- Statusにおいて取るべきActionの行動指針(戦略)を表します。
- Environment
- Agentが行動を加える対象で、行動の結果Statusの観測値とRewardをAgentに返します。
以上の設定から、離散時間$t=0, 1, 2 ...$を考えます。
ある時刻$t$に環境の状態$s(t)$を観測したエージェントは戦略$\pi$に従って行動$a(t)$を選択して実行します。行動を受けた環境は状態を$s(t+1)$へ変化させ、エージェントに報酬$r(t+1)$を返します。
ここで戦略$\pi(a|s)$は確率分布となります。受け取る報酬が最大となるような戦略$\pi$を学習するのが強化学習です。
ただ、最大化するのは即時的に得られる報酬$r(t)$ではなく、戦略によって恒久的に行動をし続けた場合に得られるだろう報酬の総額です。
つまり$r(t+1)+r(t+2)+r(t+3)+...$を考えれば良いのですが、これでは無限和になってしまいます。
そこで割引率$0<\gamma<1$を導入し、報酬の総和(利得)を次のように定義します。
R(t)=\sum^{\infty}_{k=0} \gamma^k r(t+k+1)
この利得$R(t)$の最大化を考えます。モデルでは状態、行動、報酬すべてが確率変数として扱われるため、実際に最大化するのは利得の期待値となります。
ベルマン方程式
ある戦略$\pi$を取り続け、時刻$t$で状態$s$を観測した後に得られる利得の期待値として、状態価値関数を次のように定義します。
V^{\pi}(s) = E_{P,\pi} [R(t)|s(t)=s]
この状態価値関数は、次のベルマン方程式に書き直すことができます。
V^{\pi}(s) = R^{\pi}(s) + \gamma \sum _{s'} P^{\pi} (s'|s) V^{\pi} (s')
ベルマン方程式を導入することで選択している戦略$\pi$に依存せず、状態$s$における利得を計算できるようになります。つまり、1つの環境下での最適な行動が計算できるようになります。
モデルの学習
ここまでに設定したモデルから、学習を行っていきます。学習手法で代表的なのは次の3つです。
- Value Iteration
- Policy Iteration
- Q-learning (Q-value learning)
今回の最終的な目的はDQN(Deep Q-Network)の理解なので、ここでは3つ目の「Q-learning」について勉強します。
Q-learning
状態価値関数では、状態$s$における利得の期待値を表しました。さらに、状態$s$で行動$a$を選択したときに得られる利得を次のように定義し、これを行動価値関数と呼びます。
Q^{\pi}(s, a) = E_{P} [R(t)| {\rm s}(t)=s, {\rm a}(t)=a]
この行動価値関数$Q(s,a)$はすべての行動$a$について足し合わせると、状態価値関数$V(s)$となります。
V^{\pi} (s) = \sum_{a} E_{P} [R(t), {\rm s}(t)=s | {\rm a}(t)=a]
= \sum_{a} \pi (a|s) Q^{\pi} (s,a)
ベルマン最適方程式
行動価値関数もベルマン方程式を得ることができます。
Q^{\pi}(s,a) = \sum_{s'} P(s'|s,a) R(s,a,s') + \gamma \sum_{s'} \sum_{a'} \pi (a'|s') P(s'|s,a) Q^{\pi} (s'|a')
このベルマン方程式を用いると、状態価値関数、行動価値関数より以下のようなベルマン最適方程式が得られます。
Q^{*}(s,a) = \sum _{s'} P(s'|s,a)(R(s,a,s') + \gamma max_{a' \in A(s')} Q^{*} (s',a')) \\
V^{*}(s) = max_{a \in A(s)} \sum_{s'} P(s'|s,a) (R(s,a,s') + \gamma V^{*}(s'))
ここから行動価値関数$Q(s,a)$を学習することで、最適な戦略$\pi$を見つけていきます。
学習はベルマン最適方程式を用いて、次のように表現されます。
Q^{(i+1)} (s,a) \gets Q^{(i)}(s,a) + \eta (r + \gamma max_{a'} Q^{(i)}(s',a') - Q^{(i)}(s,a))
$\eta$は学習率です。式を見るとわかりますが、報酬の期待値と見込み報酬の差分でQを更新していきます。
この差分はTD誤差(Temporal Difference)といい、このTD誤差から学習を行う方法はTD学習と呼ばれています。
上記の学習を繰り返すと、Qの値は最適行動価値関数に収束していきます。
Q^{(i)} \to Q^{*} (i \to \infty)
DQN(Deep Q-Network)
ニューラルネットワークによる学習は誤差伝搬法に基づくものです。つまり、正解との誤差をネットワークの逆方向へ伝搬させる(誤差を最小化する)ことで、モデルを正解に近づくよう調整します。
先ほど、Q-learningではTD誤差から学習していくことを学びました。この誤差を使えばQの値はニューラルネットワークで表現できそうです。
このため、まずはQ値のパラメータにおける誤差関数を定義します。
E^{(i)}(w^{(i)}) = E_{(s,a,r,s')}[1/2 (r+\gamma max_{a'} Q(s',a';w^{(i)} - Q(s,a;w^{(i)})))^{2}] \\
+ E_{(s,a)} [1/2 V_{r,s'} [(r+\gamma max_{a'} Q(s',a';w^{(i)}))^{2} | s,a]]
$w$はQのパラメータです。$r+\gamma max_{a'} Q(s',a';w^{(i)}$はアップデートされるパラメータと区別して考えます。すると、微分した際にかかる部分は第一項目の$- Q(s,a;w^{(i)})$のみとなります。
したがって、微分して得られる誤差伝搬時の勾配は以下となります。
\nabla w^{(i)} E^{(i)} (w^{(i)}) \simeq -E_{(s,a,r,s')} [(r + \gamma max_{a'} Q(s',a';w) - Q(s,a; w)) \nabla _{w^{(i)}} Q(s,a; w^{(i)})]
ここまで定義できれば、あとは勾配降下法による学習として定式化することができます。
勾配降下法の定義は以下の式です。
{w^{(i+1)}} \leftarrow {w^{(i)}} - \eta \nabla_{w^{(i)}} E^{(i)} ({w^{(i)}})
これを具体的に当てはめると、DQNにおける勾配降下法の式となります。
{w^{(i+1)}} \leftarrow {w^{(i)}} - \eta E(s,a,r,s') [(r + \gamma max_{a'} Q (s',a';w^{(i-1)}) - Q(s,a;w^{(i)})) \nabla _{w^{(i)}} Q(s,a;w^{(i)})]
実装
ざっくりと押さえたところで、実装を試してみます。
Pythonには自分で作ったAIを実際に動かして試すことのできるシミュレーション環境「gym」が提供されています。
またニューラルネットワークを容易に扱えるフレームワークであるkerasを使用して、深層強化学習のアルゴリズムを実装したライブラリ「keras-rl」がありますので、今回はこれらを組み合わせて使用します。
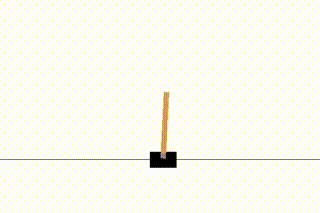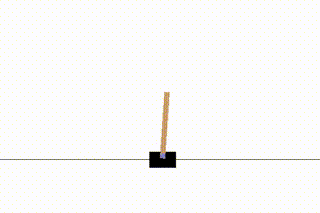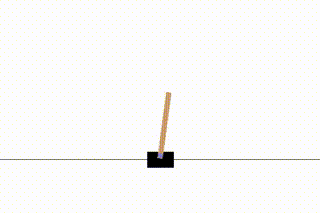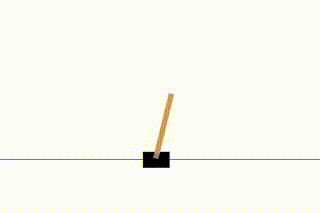
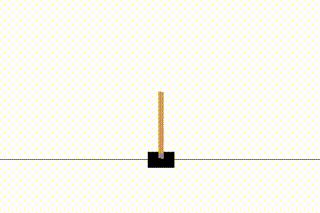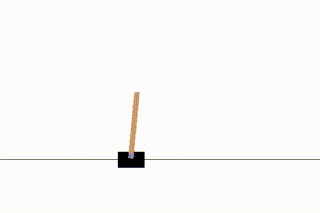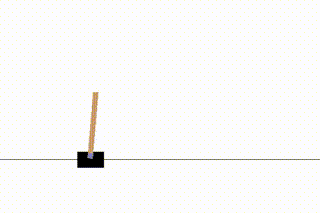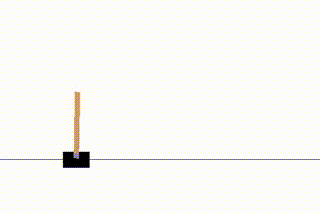
今回はgymの中から「CartPole」という、棒が倒れないようにカートを動かすというゲームを学習してみます。
「スタートしてから棒が倒れるまで」を1回のゲームとし、これをエピソードと呼びます。このエピソードを繰り返すことで学習が進んでいきます。
学習の過程は動画としてキャプチャされるので、視覚的に学習の進み具合が分かって楽しいです。
1エピソード目ではすぐに棒が倒れてしましますが、216エピソード目まで学習が進むとある程度カートが追いついていくようになります。
さらに学習を進めると、最終的には棒が倒れないモデルが得られます。
keras-rlではexampleが掲載されていて、gymに収録されているゲームであれば環境名の定義を書き換えるのみで同じコードで動きます。
import numpy as np
import gym
from keras.models import Sequential
from keras.layers import Dense, Activation, Flatten
from keras.optimizers import Adam
from rl.agents.dqn import DQNAgent
from rl.policy import BoltzmannQPolicy
from rl.memory import SequentialMemory
ENV_NAME = 'CartPole-v0'
# get environment
env = gym.make(ENV_NAME)
print(env.action_space.n)
print(env.action_space)
np.random.seed(123)
env.seed(123)
nb_actions = env.action_space.n
# define network
model = Sequential()
model.add(Flatten(input_shape=(1,) + env.observation_space.shape))
model.add(Dense(16))
model.add(Activation('relu'))
model.add(Dense(32))
model.add(Activation('relu'))
model.add(Dense(16))
model.add(Activation('relu'))
model.add(Dense(nb_actions))
model.add(Activation('linear'))
print(model.summary())
# parameter configure
memory = SequentialMemory(limit=60000, window_length=1)
policy = BoltzmannQPolicy()
dqn = DQNAgent(model=model, nb_actions=nb_actions, memory=memory, nb_steps_warmup=10,
target_model_update=1e-2, policy=policy)
dqn.compile(Adam(lr=1e-3), metrics=['mae'])
# fit
dqn.fit(env, nb_steps=50000, visualize=True, verbose=2)
# save weught
dqn.save_weights('dqn_{}_weights.h5f'.format(ENV_NAME), overwrite=True)
# test 5 episodes
dqn.test(env, nb_episodes=5, visualize=True)
今回はとりあえず動かしただけですが、gymの扱うデータ構造でゲームを定義すればkeras-rlで機械学習プログラムを組めるので、今後はgymに収録されているゲーム以外で試してみたいです。