はじめに
今回、以下の記事に触発されてこの記事を書きました。
これを参考にしました。
— 有限要素法を手に入れろ@技術書典6お01 (@tkoyama010) 2019年3月15日
Jupyter NotebookでOpenFOAMの結果をインタラクティブに可視化した https://t.co/w77ZB0zuH2 #Qiita
この記事はK3dを使って、Jupyter内でインタラクティブに可視化を行っているとても素晴らしい記事です。私もこれを読んだ後はこうなりました。
結論。Jupyter上でのvtkの出力結果の確認にはK3D-jupyterを使うべき。異論は認める。https://t.co/sdd3VH7Gzs
— 有限要素法を手に入れろ@技術書典6お01 (@tkoyama010) 2019年4月2日
GitHubを徘徊する
ただし、異論は認めるといっていることから分かるようにすっきりとはしていませんでした。理由はやはりK3DではなくmatplotlibでVTKを出力したいと考えていたからです。主な理由は以下の通りです。
- GitHubとの連携:解析したJupyterNotebookはGitHubに上げています。GitHubではJupyterNotebookをレンダリングして表示してくれるので、これを活用して解析結果を共有したいです。
- matploblib のシェア:matploblib はおそらく最もメジャーなPythonのプロットライブラリだと思います(最近はseabornやplotlyがありますが)。そのため、matplotlibでvtkファイルを出力することができれば、matplotlibに関する世界中のユーザーの知見が生かせることになります。
もやもやしながら、GitHubを徘徊していたところ、なんと本当にVTKをmatplotlibでプロットしている方を見つけました。
うわーいたよ。matplotlibでvtk表示しているおじさんが。https://t.co/bPE9aeDQsU
— 有限要素法を手に入れろ@技術書典6お01 (@tkoyama010) 2019年4月7日
meshio-example.ipynbというファイルを見てみるとmeshioというパッケージを使っていることが分かりました。そこで、このパッケージを使用してmatplotlibでPythonで使える有限要素法ライブラリgetfem++のプリ処理とポスト処理を行うことにしました。実際のJupyterNotebookはGitHubのページをご覧ください。
車輪の接触解析をやってみる
今回は2次元の簡単な例でやってみます。対象とするモデルは次の通りです。
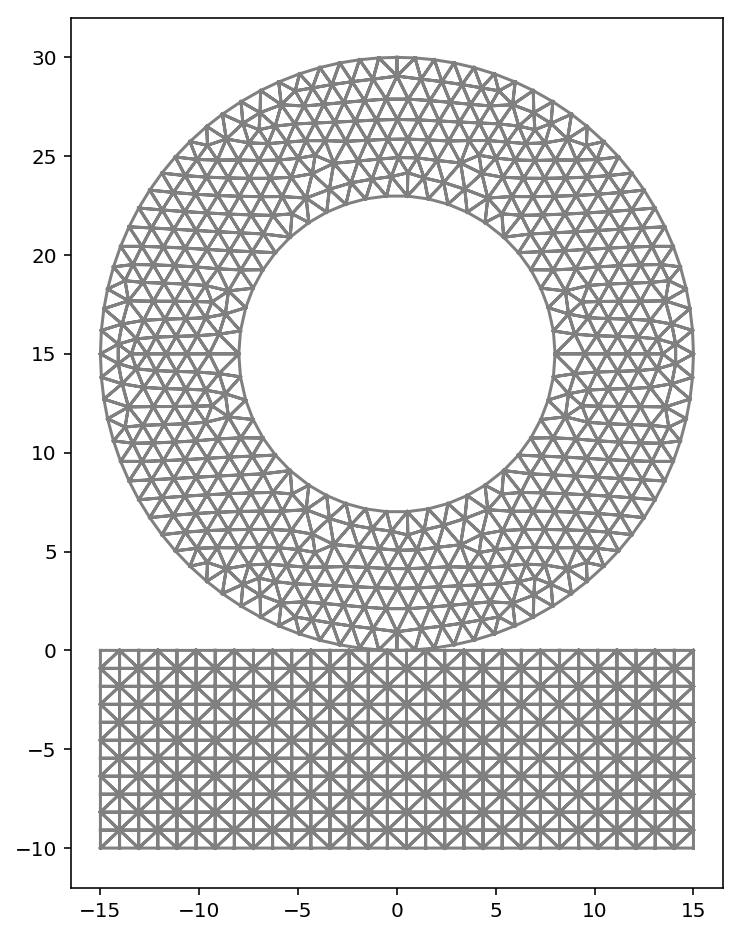
これは、地面に接触する車輪を解析する例題で最終的に、このモデルの変形とミーゼス応力を計算することが目的です。寸法は図に示す通り(単位は$cm$)で、物性値は以下の通りです。
ヤング率 $E = 21.0 \times 10^6(N/cm^2)$
ポアソン比 $\nu = 0.3$
底面は固定とし、穴の部分に $1 \times 10^7N/cm^2$ の力がかかっているとします。接触条件の処理などについては、wheel.ipynbに書かれていますので、そちらをご覧ください。
このメッシュ図の描き方ですが。GetFEM++のMesherオブジェクトを使用して、Meshオブジェクトを作成して描いています。メッシュ作成の流れは以下の通りです。
車輪
- Mesherオブジェクトで幾何情報を設定する。大きな'ball'のMesherオブジェクトmo1と、小さな'ball'のMesherオブジェクトmo2を作成する。
車輪の部分
wheel.ipynbの解析を実行すると次のような結果が得られます。
結果の値が分からないと意味ないので、ミーゼス応力のコンターバーつけました。#GetFEM pic.twitter.com/82D80JcfJl
— 有限要素法を手に入れろ@技術書典6お01 (@tkoyama010) 2019年4月8日
まとめ
こうなりました。
結論。Jupyter上でのvtkの出力結果の確認にはmeshioとmatplotlibを使うべき。異論は認めない。 #GetFEMhttps://t.co/lwNMph1lt4 https://t.co/wkVN38PpgK
— 有限要素法を手に入れろ@技術書典6お01 (@tkoyama010) 2019年4月7日
Jupyter-Notebookで有限要素法のプリ・解析・ポストが全てできましたので、以下のような活用法が考えられます。
- 条件を変えて解析をしたいときは新しくブランチを作成してシミュレーションを行う。行ったシミュレーションはGitHubにPushすることで共有ができる。
- Jupyter-NotebookはPythonの文書作成ツールsphinxと連携が可能なので、masterブランチにドキュメントのテンプレートとなる報告書をmasterに置いておけば異なる条件で同じ形式の報告書を作成することが可能になる。