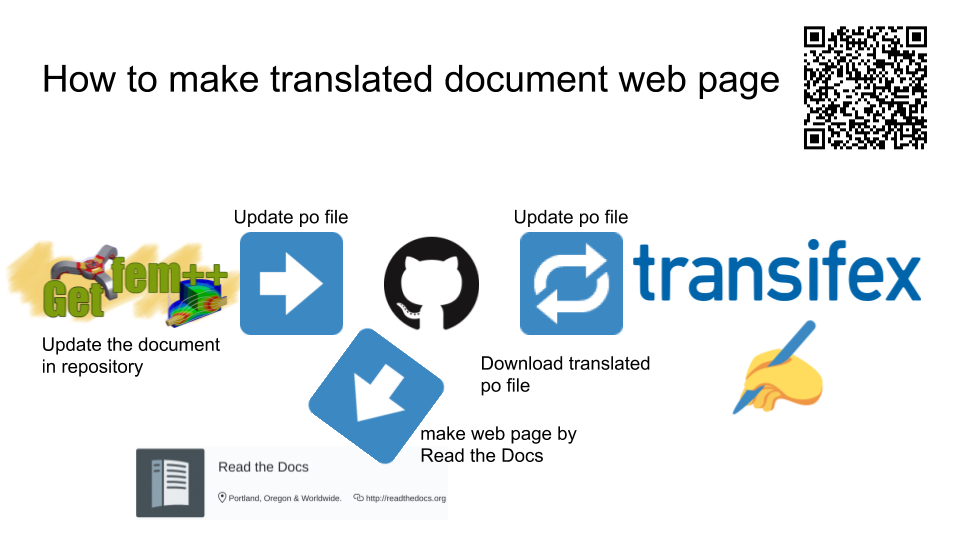
はじめに
GetFEM++は、共同開発をベースにしたオープンソースライブラリーです。有限要素法を解くための最も柔軟なフレームワークを提供することを目的としています。有限要素を用いた線形および非線形偏微分方程式のシステムを呼び出すことができます。2019年のGetFEM++プロジェクトへの貢献について報告します。
翻訳
新しいコントリビューターがドキュメントを翻訳するための推奨方法は、TransifexのGetFEM翻訳チームに参加することです。投稿はtransifexでアカウントを作成し、リクエスト言語と記入フォームをクリックしてください。翻訳後、transifex-clientを使用して翻訳されたpoファイルをサイトからプルします。transifexサイトで入手できるapiトークンが必要です。
$ git clone https://git.savannah.nongnu.org/git/getfem.git
$ cd getfem/doc/sphinx
$ tx pull -l <lang>
母国語のコードを <lang> に設定します(Sphinxで現在サポートされている言語を参照してください。)。トラブルが発生するため、Transifexにはプッシュしないでください。チームページでファイルを1つずつアップロードできます。変換されたpoファイルをプルした後、doc/sphinx/Makefile.amで <lang> をLANGUAGEに設定します。
LANGUAGE = <lang>
SPHINXOPTS = -D language=\$(LANGUAGE)
その後、次のコマンドを実行して、htmlの地域化されたドキュメントを作成できます。
$ cd doc/sphinx
$ make html
使用している言語でpdfファイルを作成するには、
$ make latex
$ cd build/latex
$ make all-pdf-<lang>
詳細については、Sphinx Internationalizationを参照してください。ドキュメントをTransifexで翻訳すると、Read the Docs に自動的に表示されます。
チュートリアル
このセクションでは、リポジトリに追加したチュートリアルについて説明します。問題は半径1.0の円の中にLapacianと呼ばれる微分方程式を仮定します。
$$- \Delta u = 1 \ {\rm in}\ \Omega$$
$\Omega$は円の中の面積を意味します。方程式のRHSは$1.0$です。これは円の上に荷重があることを意味します。$\partial\Omega$を計算する$\Omega$側のuの値は0です。
$$u = 0 \ {\rm in}\ \delta \Omega$$
最初に、MesherObjectを使用して円のジオメトリを作成します。ジオメトリの形および座標の中心として文字列'ball'と半径の大きさを引数に設定します。理論解を計算するためには、ジオメトリの中心座標は $(0.0、0.0)$ に設定する必要があります。ただし、MeserObjectは負の値を設定できません。そこで、まずは中心が$(1.0、1.0)$であるメッシュを作成します。要素の次数は2に設定します。
# Import basic modules
import getfem as gf
## Parameters
h = 0.1 # approximate diameter of the elements.
# Create a unit disk mesh
mo = gf.MesherObject('ball', [1.0, 1.0], 1.0)
MesherObjectを使用してMeshオブジェクトを作成できます。
mesh = gf.Mesh('generate', mo, h, 2)
メッシュを作成した後、translateメソッドを使用して中心座標を$(0.0、0.0)$に移動します。
mesh.translate([-1.0, -1.0])
FemオブジェクトをMeshオブジェクトにリンクし、MeshFemオブジェクトをMeshオブジェクトと節点の自由度によって作成します。次に、set_classical_femメソッドを使用して古典的Lagrange要素を設定します。
# Create a MeshFem for u and rhs fields of dimension 1
mfu = gf.MeshFem(mesh, 1)
mfrhs = gf.MeshFem(mesh, 1)
# assign the Classical Fem
elements_degree = 2
mfu.set_classical_fem(elements_degree)
mfrhs.set_classical_fem(elements_degree)
また,積分法をMeshオブジェクトにリンクし,MeshImオブジェクトを作成する。
# Integration method used
mim = gf.MeshIm(mesh, pow(elements_degree,2))
境界条件を設定するために、外側境界領域を設定します。outer_facesメソッドを使用して外側の面を取得します。
# Boundary selection
flst = mesh.outer_faces()
# Mark it as boundary
DIRICHLET_BOUNDARY = 1
mesh.set_region(DIRICHLET_BOUNDARY, flst)
Modelオブジェクトを作成し、連立方程式を作成します。
# Model
md = gf.Model('real')
連立方程式の未知変数としてMeshFemオブジェクトを設定します。
# Main unknown
md.add_fem_variable('u', mfu)
PDE、RHSと条件の項をModelオブジェクトに加えます。
# Laplacian term on u
md.add_Laplacian_brick(mim, 'u')
# Volumic source term
F = mfrhs.eval('1')
md.add_initialized_fem_data('VolumicData', mfrhs, F)
md.add_source_term_brick(mim, 'u', 'VolumicData')
# Dirichlet condition on the boundary.
md.add_Dirichlet_condition_with_multipliers(
mim, 'u', elements_degree - 1, DIRICHLET_BOUNDARY
)
Modelオブジェクトを作成した後、連立方程式を解きます。uの値をエクスポートします。
# Assembly of the linear system and solve.
md.solve()
# Main unknown
U = md.variable('u')
この問題の理論的な解は次の通りです。
$$
u = \frac{1-x^2-y^2}{4}
$$
evalメソッドを用いて理論解を計算することができます。
# Interpolate the exact solution
Ue = mfu.eval('(1-x*x-y*y)/4')
GetFEM++の結果は以下になります。
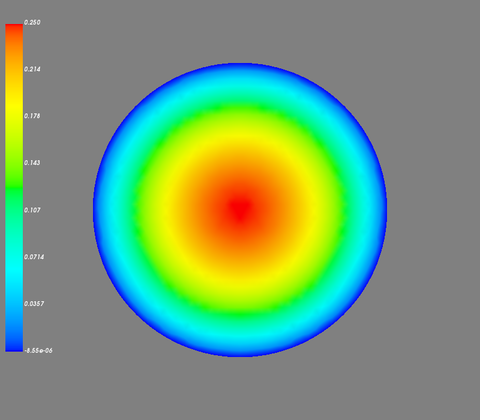
理論解の結果は以下になります。
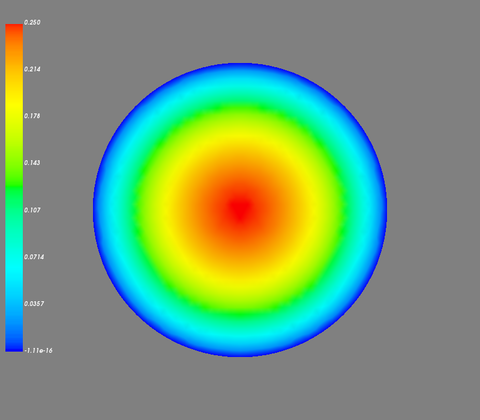
集中質量行列
集中質量行列は時刻歴解析の陽解法に一般的に使用されます。GetFEM++では、Modelオブジェクトに分布質量のブリックを追加できます。しかし、集中質量ブリックを追加することはできません。そこで、lumped_mass_brick_for_first_orderオブジェクトを追加しました。ブリッククラスの継承関係は、下図を参照してください。
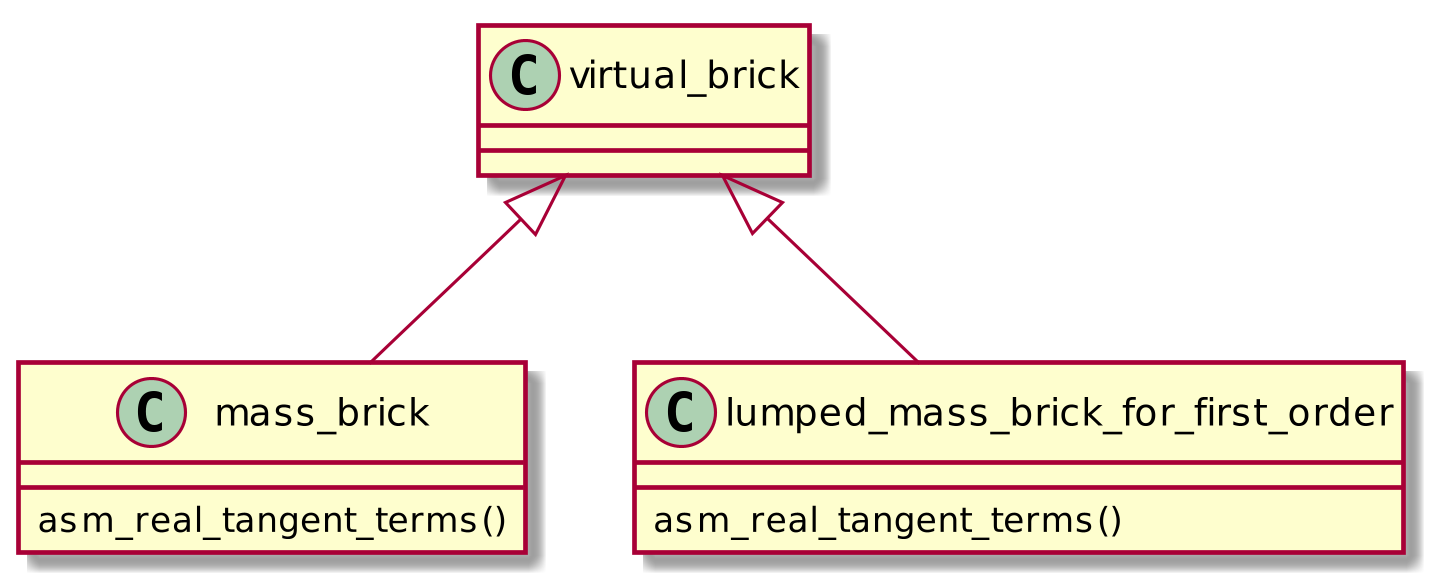
このブリックを変数に追加するには、C++のAPIの場合、次のようにします。
add_lumped_mass_brick_for_first_order(model &md, const mesh_im &mim, const std::string &varname);
実装は次の通りです。
// ----------------------------------------------------------------------
//
// Lumped Mass brick for first order
//
// ----------------------------------------------------------------------
struct lumped_mass_brick_for_first_order : public virtual_brick {
virtual void asm_real_tangent_terms(const model &md, size_type,
const model::varnamelist &vl,
const model::varnamelist &dl,
const model::mimlist &mims,
model::real_matlist &matl,
model::real_veclist &,
model::real_veclist &,
size_type region,
build_version) const {
GMM_ASSERT1(matl.size() == 1,
"Lumped Mass brick has one and only one term");
GMM_ASSERT1(mims.size() == 1,
"Lumped Mass brick needs one and only one mesh_im");
GMM_ASSERT1(vl.size() == 1 && dl.size() <= 1,
"Wrong number of variables for lumped mass brick");
const mesh_fem &mf_u = md.mesh_fem_of_variable(vl[0]);
const mesh &m = mf_u.linked_mesh();
const mesh_im &mim = *mims[0];
mesh_region rg(region);
m.intersect_with_mpi_region(rg);
const mesh_fem *mf_rho = 0;
const model_real_plain_vector *rho = 0;
if (dl.size()) {
mf_rho = md.pmesh_fem_of_variable(dl[0]);
rho = &(md.real_variable(dl[0]));
size_type sl = gmm::vect_size(*rho);
if (mf_rho) sl = sl * mf_rho->get_qdim() / mf_rho->nb_dof();
GMM_ASSERT1(sl == 1, "Bad format of mass brick coefficient");
}
GMM_TRACE2("Lumped mass matrix assembly (please check that integration is 1st order.)");
gmm::clear(matl[0]);
if (dl.size() && mf_rho) {
asm_lumped_mass_matrix_for_first_order_param(matl[0], mim, mf_u, *mf_rho, *rho, rg);
} else {
asm_lumped_mass_matrix_for_first_order(matl[0], mim, mf_u, rg);
if (dl.size()) gmm::scale(matl[0], (*rho)[0]);
}
}
lumped_mass_brick_for_first_order() {
set_flags("Lumped mass brick", true /* is linear*/,
true /* is symmetric */, true /* is coercive */,
true /* is real */, false /* no complex version */,
false /* compute each time */);
}
};
size_type add_lumped_mass_brick_for_first_order
(model & md, const mesh_im &mim, const std::string &varname,
const std::string &dataexpr_rho, size_type region) {
pbrick pbr = std::make_shared<lumped_mass_brick_for_first_order>();
model::termlist tl;
tl.push_back(model::term_description(varname, varname, true));
model::varnamelist dl;
if (dataexpr_rho.size())
dl.push_back(dataexpr_rho);
return md.add_brick(pbr, model::varnamelist(1, varname), dl, tl,
model::mimlist(1, &mim), region);
}
asm_real_tangent_termsを計算するために、関数asm_lumped_mass_matrix_for_first_orderも追加しました。この関数では,整合質量ブリックを計算し,単位ベクトルを乗算して集中質量の対角項を計算します。この方法は1次の要素に対してのみ有効です。そこで、名前に_for_first_orderを追加しました。ソースコードは以下の通りです。
/**
lumped mass matrix assembly from consistent mass matrix
*/
template<typename MAT>
inline void asm_lumped_mass_matrix_for_first_order_from_consistent
(const MAT &M) {
size_type nbd = gmm::mat_ncols(M), nbr = gmm::mat_nrows(M);
GMM_ASSERT1(nbd == nbr, "mass matrix is not square");
typedef typename gmm::linalg_traits<MAT>::value_type T;
std::vector<T> V(nbd), W(nbr);
gmm::fill(V, T(1));
gmm::mult(M, V, W);
gmm::clear(const_cast<MAT &>(M));
for (size_type i =0; i < nbd; ++i) {
(const_cast<MAT &>(M))(i, i) = W[i];
}
}
/**
lumped mass matrix assembly (on the whole mesh or on the specified
boundary)
@ingroup asm
*/
template<typename MAT>
inline void asm_lumped_mass_matrix_for_first_order
(const MAT &M, const mesh_im &mim, const mesh_fem &mf1,
const mesh_region &rg = mesh_region::all_convexes()) {
asm_mass_matrix(M, mim, mf1, rg);
asm_lumped_mass_matrix_for_first_order_from_consistent(M);
}
/**
lumped mass matrix assembly with an additional parameter
(on the whole mesh or on the specified boundary)
@ingroup asm
*/
template<typename MAT, typename VECT>
inline void asm_lumped_mass_matrix_for_first_order_param
(MAT &M, const mesh_im &mim, const mesh_fem &mf_u, const mesh_fem &mf_data,
const VECT &F, const mesh_region &rg = mesh_region::all_convexes()) {
asm_mass_matrix_param(M, mim, mf_u, mf_data, F, rg);
asm_lumped_mass_matrix_for_first_order_from_consistent(M);
}
Houbolt法
過渡応答解析を積分するためのschemeを追加しました。これは次のような問題です。
$$
(K+\frac{11}{6 dt}C+\frac{2}{dt^2}M) u_{n} = F_{n} + (\frac{5}{dt^2} M + \frac{3}{ dt} C) u_{n-1}
- (\frac{4}{dt^2} M + \frac{3}{2 dt} C) u_{n-2}
- (\frac{1}{dt^2} M + \frac{1}{3 dt} C) u_{n-3}
$$
ここで、$dt$は時間ステップ、$M$はDot2_uの質量マトリックスです。$C$はDot_uの減衰行列、$K$はuの項の剛性行列です。この方法をHoubolt法と呼びます。Affine依存関係は次のようになります。
# Dot_u = 1/(6*dt)*(11*u-18*Previous_u+9*Previous2_u-2*Previous3_u)}
# Dot2_u = 1/(dt**2)*(2*u-5*Previous_u+4*Previous2_u-Previous3_u)}
このschemeをModelオブジェクトの変数${\tt u}$に適用すると、Affine従属変数Dot_u、Dot2_uがModelオブジェクトに追加されます。これは、変数の1階および2階の時間微分を表し、ブリックで追加した要素に対し使用できます。変数 Previous_u , Previous2_u, Previous3_u も追加されます。これは時間ステップn-1,n-2,n-3での u の値に対応します。求解の前に、データPrevious_u、Previous2_u、Previous3_u ($U^0$に対応します)を初期化する必要があります。クラスの継承関係を図に示します。
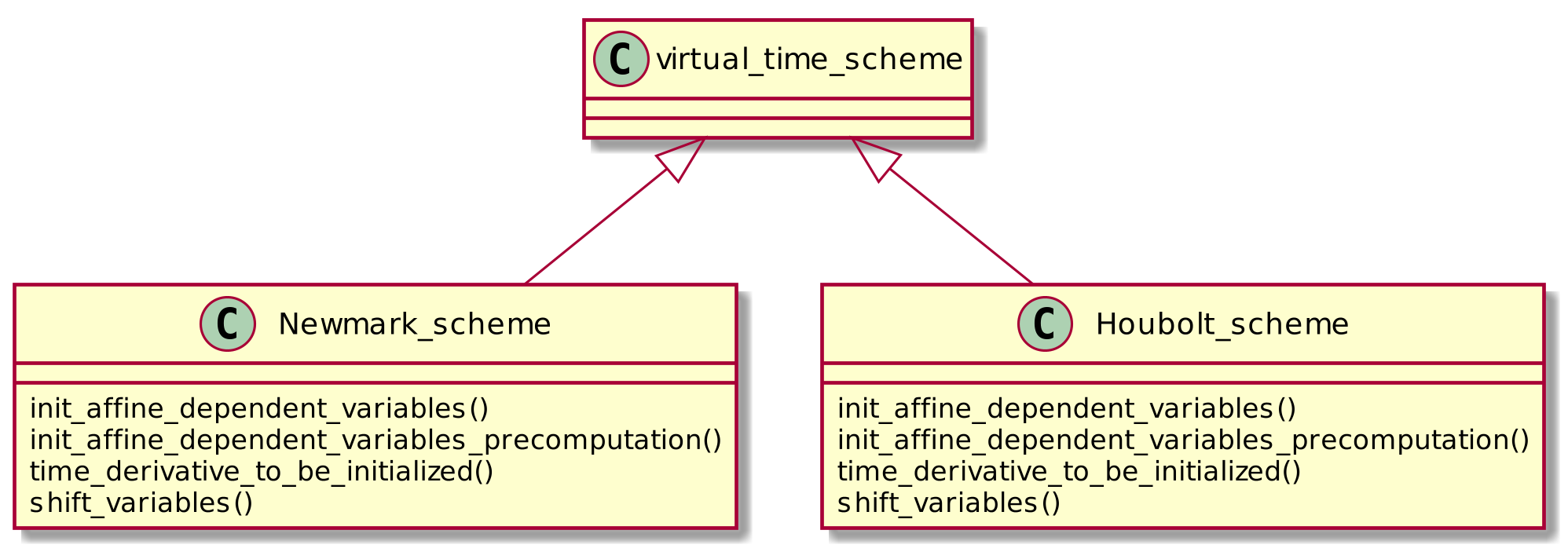
このschemeを変数に追加するには、C++のAPIの場合
add_Houbolt_scheme(model &md, const std::string &varname);
とします。実装は次の通りです。
// ----------------------------------------------------------------------
//
// Houbolt method
//
// ----------------------------------------------------------------------
class APIDECL Houbolt_scheme
: public virtual_time_scheme {
std::string U, U01, U02, U03, V, A;
public:
// V = 1/(6*dt)*(11*U-18*U01+9*U02-2*U03)
// A = 1/(dt**2)*(2*U-5*U01+4*U02-U03)
virtual void init_affine_dependent_variables(model &md) const {
scalar_type dt = md.get_time_step();
scalar_type a0 = scalar_type(2)/(dt*dt);
scalar_type a1 = scalar_type(5)/(dt*dt);
scalar_type a2 = scalar_type(4)/(dt*dt);
scalar_type a3 = scalar_type(1)/(dt*dt);
scalar_type b0 = scalar_type(11)/(scalar_type(6)*dt);
scalar_type b1 = scalar_type(18)/(scalar_type(6)*dt);
scalar_type b2 = scalar_type(9)/(scalar_type(6)*dt);
scalar_type b3 = scalar_type(2)/(scalar_type(6)*dt);
md.set_factor_of_variable(V, b0);
md.set_factor_of_variable(A, a0);
if (md.is_complex()) {
gmm::add(gmm::scaled(md.complex_variable(U01), -complex_type(b1)),
gmm::scaled(md.complex_variable(U02), complex_type(b2)),
md.set_complex_constant_part(V));
gmm::add(gmm::scaled(md.complex_variable(U03), -complex_type(b3)),
md.set_complex_constant_part(V));
gmm::add(gmm::scaled(md.complex_variable(U01), -complex_type(a1)),
gmm::scaled(md.complex_variable(U02), complex_type(a2)),
md.set_complex_constant_part(A));
gmm::add(gmm::scaled(md.complex_variable(U03), -complex_type(a3)),
md.set_complex_constant_part(A));
} else {
gmm::add(gmm::scaled(md.real_variable(U01), -b1),
gmm::scaled(md.real_variable(U02), b2),
md.set_real_constant_part(V));
gmm::add(gmm::scaled(md.real_variable(U03), -b3),
md.set_real_constant_part(V));
gmm::add(gmm::scaled(md.real_variable(U01), -a1),
gmm::scaled(md.real_variable(U02), a2),
md.set_real_constant_part(A));
gmm::add(gmm::scaled(md.real_variable(U03), -a3),
md.set_real_constant_part(A));
}
}
virtual void init_affine_dependent_variables_precomputation(model &md)
const {
(void) md;
}
virtual void time_derivative_to_be_initialized
(std::string &name_v, std::string &name_previous_v) const {
(void) name_v;
(void) name_previous_v;
}
virtual void shift_variables(model &md) const {
if (md.is_complex()) {
gmm::copy(md.complex_variable(U02), md.set_complex_variable(U03));
gmm::copy(md.complex_variable(U01), md.set_complex_variable(U02));
gmm::copy(md.complex_variable(U), md.set_complex_variable(U01));
} else {
gmm::copy(md.real_variable(U02), md.set_real_variable(U03));
gmm::copy(md.real_variable(U01), md.set_real_variable(U02));
gmm::copy(md.real_variable(U), md.set_real_variable(U01));
}
}
Houbolt_scheme(model &md, std::string varname) {
U = varname;
U01 = "Previous_" + U;
U02 = "Previous2_" + U;
U03 = "Previous3_" + U;
V = "Dot_" + U;
A = "Dot2_" + U;
if (!(md.variable_exists(V)))
md.add_affine_dependent_variable(V, U);
if (!(md.variable_exists(A)))
md.add_affine_dependent_variable(A, U);
const mesh_fem *mf = md.pmesh_fem_of_variable(U);
size_type s = md.is_complex() ? gmm::vect_size(md.complex_variable(U))
: gmm::vect_size(md.real_variable(U));
if (mf) {
if (!(md.variable_exists(U01))) md.add_fem_data(U01, *mf);
if (!(md.variable_exists(U02))) md.add_fem_data(U02, *mf);
if (!(md.variable_exists(U03))) md.add_fem_data(U03, *mf);
} else {
if (!(md.variable_exists(U01))) md.add_fixed_size_data(U01, s);
if (!(md.variable_exists(U02))) md.add_fixed_size_data(U02, s);
if (!(md.variable_exists(U03))) md.add_fixed_size_data(U03, s);
}
}
};
void add_Houbolt_scheme(model &md, const std::string &varname) {
ptime_scheme ptsc = std::make_shared<Houbolt_scheme>
(md, varname);
md.add_time_integration_scheme(varname, ptsc);
}
まとめ
2019年のGetFEM++への貢献を報告しました。以下の貢献を行いました。
- 引き続きドキュメントの日本語化を行いました。
- 紹介したチュートリアルをリポジトリに追加しました。
-
lumped_mass_brick_for_first_orderオブジェクトを追加しました。 -
Houbolt_schemeオブジェクトを追加しました。
今年のコミット数は46でした。ここで、紹介した以外のコントリビューションについてはリポジトリをご参照ください。