はじめに ー 週末研究ノートとは?
個人的に研究的な活動をやるにあたり、オープンにしてみたら面白いかもと思い、自分が興味を持っている ざっくりテーマについて、これから、ゆるい週末研究を公開していこうと思います。(有識者の方のアドバイスも、ちょっとというかかなり期待してます!笑)
どこかの権威的な学会やジャーナルなどで発表する予定はないため、万が一、私の記事を利用する際には自己責任でお願いします。そんな人はいないと思いますが、念のため。
今回のサマリ (TL; DR)
任意の分布関数からサンプリングする方法を実際に試しました。
環境
- Colaboratory
- コードは、こちら
今回の週末研究ノート
今回は、任意の分布からサンプリングってできるはずだけど、どうやるんだっけ?を調査し実機で確認しました。
よく確率密度関数とか頑張って計算してるのを見るけど、そこからサンプリングできるイメージがわかないと、何やってるんだっけってなる。そう、迷子になります笑
がんばって計算してるけど・・・で?ってなる笑
棄却サンプリング
今回は、比較的シンプルな棄却サンプリングを調査し試しました。
棄却サンプリングは、確率密度関数$P(x)$とその上限がわかっていること(より正確には、一様に上から抑えられる関数$Q(x)$が定義できること; i.e. $\forall x, P(x) \le Q(x)$)が前提です。詳細は、参考文献を参照ください。
ざっくりいうと、乱数$rx$ に対して、 $\frac{P(rx)}{Q(rx)}$ の確率で、その乱数$rx$ を採用し、そうでない場合に棄却して、サンプリングを残す方法です。
特に、$P(x)$ は、規格化されている必要がない、という点もかなり利便性が高いです。
ここでは、扱いやすくおそらく汎用的に使えると思われる $Q(x)$ が定数関数($Q(x) = k$)の場合を前提として、実際に実機で確かめてみます。
実際に試してみる
早速、コードを見ていきましょう。
正規分布風 P(x)
import numpy
from matplotlib import pyplot
rs = numpy.random.RandomState(12345)
rs
$P(x), Q(x)$ を以下のように定義しておきます。
# P(x)
def pdf_fake_normal(x, mu, sigma):
return numpy.exp(-0.5 * ((x - mu) / sigma) ** 2)
# Q(x)
def qdf_const(x, k=1):
return k * numpy.ones_like(x)
サンプリングする関数を、以下のように定義します。最後の$px$ が求めるサンプリング結果です。(i.e. 分布$P(x)$ からのサンプリング結果です)
def sampler(pdf, qdf, a=5, N=10000):
rx = rs.uniform(-a, a, size=N)
p = pdf(rx)
q = qdf(rx)
u = q * rs.uniform(0, 1, size=q.shape)
px = rx[u <= p]
return px
便利のために、密度関数の$x, y=P(x)$を生成する関数を定義しておきます。
def target_maker(pdf, a):
x = numpy.linspace(-a, a)
_y = pdf(x)
y = _y / (_y.sum() * numpy.abs(x[0] - x[1]))
return x, y
実際に、サンプリングするコードは、以下の通りです。pdf, qdf を定義して、sampler を実行します。
%%time
N = 10000
a = 5
pdf = lambda x: pdf_fake_normal(x, mu=0, sigma=1)
qdf = lambda x: qdf_const(x, k=pdf(0))
px = sampler(pdf, qdf, a, N)
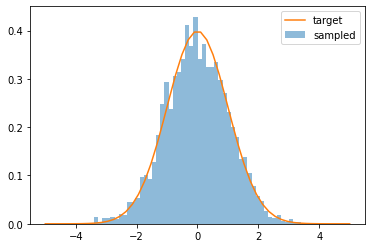
以下のコードで、密度関数とサンプルした乱数のヒストグラムをプロットして、正しくサンプリングできたかをグラフで確認します。
x, y = target_maker(pdf, a)
pyplot.hist(px, bins=50, density=True, alpha=0.5, label='sampled')
pyplot.plot(x, y, label='target')
pyplot.legend()
pyplot.show()
すばらしい! まさに正規分布です!!
P(x) = x^2
今度は、分布 $P(x) := x^2$ からサンプリングしてみます。
$P(x)$ は、以下のように定義します。
def pdf_x_squared(x: numpy.ndarray):
return x ** 2
先ほどと同様にして、サンプリングします。pdf と、qdf を定義するパラメータ$k$ が異なっています。
%%time
N = 10000
a = 5
pdf = lambda x: pdf_x_squared(x)
qdf = lambda x: qdf_const(x, k=pdf(a))
px = sampler(pdf, qdf, a, N)
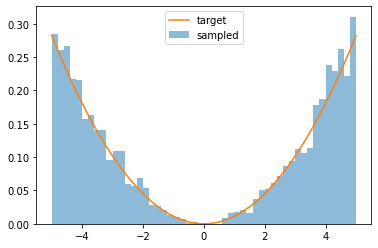
先ほどと同様に、密度関数とサンプルした乱数のヒストグラムをプロットして、正しくサンプリングできたかを確認します。
x, y = target_maker(pdf, a)
pyplot.hist(px, bins=50, density=True, alpha=0.5, label='sampled')
pyplot.plot(x, y, label='target')
pyplot.legend()
pyplot.show()
おー!、それっぽい!!
成功ですね!
まとめ
以上のように、任意の分布からサンプリングする方法を実機で確認し、確かにサンプリングできることがわかりました。
これで、分布関数をがんばって式変形する意味がわかります!笑