目的
ベイズ推論による機械学習入門の勉強用のノート。
式を後で参照するために残しておく。
関連
ベイズ推論の勉強用ノート(1)ー 基本的な定義
ベイズ推論の勉強用ノート(2)ー 離散確率分布
ベイズ推論の勉強用ノート(3)ー 連続確率分布
ベイズ推論の勉強用ノート(4)ー 事後分布の推定
予測分布
パラメータが学習されたあと、パラメータの分布を使って、
未観測データ$x_* $ の予測分布$p(x_*|D)$を推定する
\begin{align}
p(x_*|D)
&= \int p(x_*|\theta)p(\theta|D)d\theta \\
&= \langle p(x_*|\theta) \rangle_{p(\theta|D)} \\
\end{align}
上記式は、確率分布 $p(x_*|\theta)$ の $p(\theta|D)$ による加重平均(期待値)を意味している。
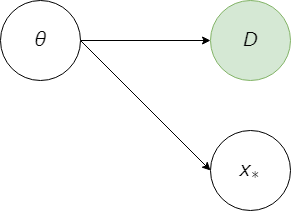
このモデルの関係をグラフィカルモデルで表すと以下の図のようになる。
このモデルでは、データ$D$、未知のデータ$x_*$ のいずれも、パラメータ(ベクトル)$\theta$ によって決定されることを表している。
特に、$D$、$x_*$ の間には、直接的な依存関係は仮定していない点にも留意する。つまり、パラメータが与えられたもとで、独立である。 (式で表すと以下の通り。)
p(D, x_*|\theta) = p(D|\theta)p(x_*|\theta)
このグラフィカルモデルが表している同時分布は以下のようになる。
\begin{align}
p(D, x_*, \theta) = p(D|\theta)p(x_*|\theta)p(\theta)
\end{align}
データ$D$が観測された後の、事後分布を計算すると以下のようになる。
\begin{align}
p(x_*, \theta|D)
&= \frac{p(D, x_*, \theta)}{p(D)} \\
&= \frac{p(D|\theta)p(x_*|\theta)p(\theta)}{p(D)} \\
&= \frac{p(x_*|\theta)p(D|\theta)p(\theta)}{p(D)} \\
&= p(x_*|\theta)p(\theta|D) \\
\end{align}
ここで、この事後分布 $p(x_*, \theta|D)$ を、$\theta$ で周辺化した分布が、
予測分布$p(x_*|D)$になることに注意しておく。
つまり、
\begin{align}
p(x_*|D)
&= \int p(x_*, \theta|D)d\theta \\
&= \int p(x_*|\theta)p(\theta|D)d\theta \\
\end{align}
である。
また、データ$D$が、まったく観測されていない場合は、以下のように予測することもできる。
\begin{align}
p(x_*)
&= \int p(x_*, \theta)d\theta \\
&= \int p(x_*|\theta)p(\theta)d\theta \\
\end{align}