はじめに ー 週末研究ノートとは?
個人的に研究的な活動をやるにあたり、オープンにしてみたら面白いかもと思い、自分が興味を持っている ざっくりテーマについて、これから、ゆるい週末研究を公開していこうと思います。(有識者の方のアドバイスも、ちょっとというかかなり期待してます!笑)
どこかの権威的な学会やジャーナルなどで発表する予定はないため、万が一、私の記事を利用する際には自己責任でお願いします。そんな人はいないと思いますが、念のため。
今回のサマリ (TL; DR)
気がついたら年末になってしまいましたが、大学院修了後に導出した論理学×位相数学の理論的な結果の中で、位相空間に閉じた結果のみを抽出して掲載します。
連続写像と開集合系の交叉関係に深い関係性があることを定理として証明しました。
環境
- なし
今回の週末研究ノート
以下の章立てで記載していきます
- 位相空間に関する定義
- 連続開写像と開集合系の交叉関係
- 開集合系の交叉関係が作る写像
- 連続開写像が作る開集合系の交叉関係
- 連続写像と開集合系の交叉関係
位相空間に関する定義
開集合系
\begin{aligned}
O:& an~open~system~forX \\
\overset{def}{\Leftrightarrow} & ~O \subseteq \mathcal{P}(X),~which \\
&(i) ~\emptyset, X \in O \\
&(ii) ~u_1, u_2 \in O \Rightarrow u_1 \cap u_2 \in O \\
&(iii) ~\{u_{\lambda}\}_{\lambda \in \Lambda} \in O \Rightarrow \cup \{u_{\lambda}\}_{\lambda \in \Lambda} \in O \\
\end{aligned}
ここで、$\mathcal{P}(X)$ は、集合$X$のべき集合とする。
連続写像
\begin{aligned}
\langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
\\
f:& X \rightarrow X'; ~continuous~(on~X) \\
&\overset{def}{\Leftrightarrow} \forall u' \in O', f^{-1}(u') \in O \\
\end{aligned}
ここで、当該連続写像の定義は、選択公理が成り立つことを前提としている点に注意する。
開写像
\begin{aligned}
\langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
\\
f:& X \rightarrow X'; ~open \\
&\overset{def}{\Leftrightarrow} \forall u \in O, f(u) \in O' \\
\end{aligned}
独自定義
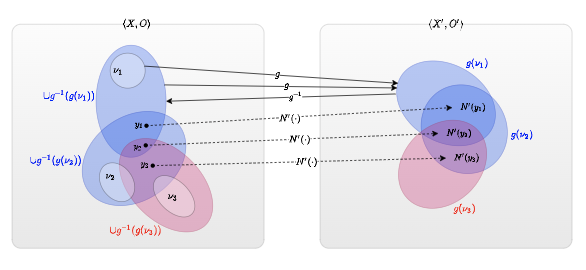
ここで、表現を簡易にするために独自に定義を導入しておく。
\begin{aligned}
& \langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
& g: O \rightarrow O'; given \\
\\
& For ~ \forall y \in X, Let ~ N'(y) ~ be~as~bellow: \\
& ~~~~ N'(y) := \underset{v: ~ y \in \cup g^{-1}(g(v))}{\bigcap} g(v) \cap \underset{v: ~ y \notin \cup g^{-1}(g(v))}{\bigcap} g(v)^{\mathsf{c}} \\
\\
& where ~ \cup g^{-1}(g(v)) := \bigcup_u \{ u \in O | g(u) = g(v) \} \subseteq X
\end{aligned}
同様に
\begin{aligned}
& For ~ \forall y' \in X', Let ~ N(y') ~ be~as~bellow: \\
& ~~~~ N(y') := \underset{v: ~ y' \in g(v)}{\bigcap} \cup g^{-1}(g(v)) \cap \underset{v: ~ y' \notin g(v)}{\bigcap} \cup g^{-1}(g(v))^{\mathsf{c}} \\
\end{aligned}
上記の定義について補足すると、
$N'(y)$ は、 $X'$ 上の($y \in X$ に対する)類似要素の集合を意味し、かつ、開集合系上の写像$g$ によって対応付けられた集合の共通部分により類似要素の集合を構成(同じ交叉関係にある集合を特定)している。 $N(y')$ についても、同様に解釈する。
特に、$f: X \rightarrow X'$ に対しても、同様に定義することができる。
具体的には、以下のように定義する。
\begin{aligned}
& Let ~ f: X \rightarrow X' \\
\\
& For ~ \forall y \in X, Let ~ N_f'(y) ~ be~as~bellow: \\
& ~~~~ N_f'(y) := \underset{v: ~ y \in f^{-1}(f(v))}{\bigcap} f(v) \cap \underset{v: ~ y \notin f^{-1}(f(v))}{\bigcap} f(v)^{\mathsf{c}} \\
\end{aligned}
\begin{aligned}
& For ~ \forall y' \in X', Let ~ N_f(y') ~ be~as~bellow: \\
& ~~~~ N_f(y') := \underset{v: ~ y' \in f(v)}{\bigcap} f^{-1}(f(v)) \cap \underset{v: ~ y' \notin f(v)}{\bigcap} f^{-1}(f(v))^{\mathsf{c}} \\
\end{aligned}
ここで、$N(y')$ と $N_f(y')$ および $N'(y)$ と $N_f'(y)$ は、それぞれ対応し、$X$(もしくは、$X'$)上の集合上では、写像$f$ を $g$ の写像化したものとして解釈・定義することで同じ構造として、みなすことができる点に注意する。(以降の証明では、この定義を使う。)
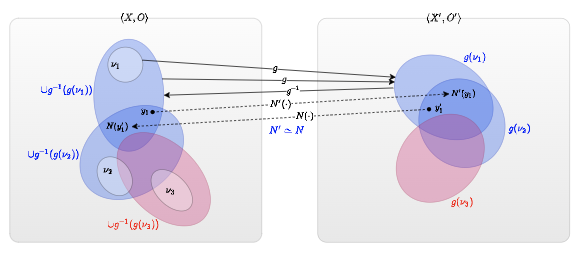
補題
ここで、上記定義における、2つの一般位相空間上の関係を述べる。
\begin{aligned}
& \langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
& g: O \rightarrow O' \\
\\
& For ~ \forall y \in X, \forall y' \in X' \\
& ~~~~ y \in N(y') \Leftrightarrow y' \in N'(y) \\
\end{aligned}
証明を以下に示す。
\begin{aligned}
For ~ \forall y \in X, \forall y' \in X', \\
~~~~ y \in & N(y') \\
\Leftrightarrow & ~~~~ \forall v \in O, \\
& ~~~~~~~~ if ~ y' \in g(v), ~ then ~ y \in \cup g^{-1}(g(v)) \\
& ~~~~~~~~ if ~ y' \notin g(v), ~ then ~ y \in \cup g^{-1}(g(v))^{\mathsf{c}} \\
\Leftrightarrow & ~~~~ \forall v \in O, y' \in g(v) \leftrightarrow y \in \cup g^{-1} (g(v)) \\
\Leftrightarrow & ~~~~ \forall v \in O, \\
& ~~~~~~~~ if ~ y \in \cup g^{-1}(g(v)), ~ then ~ y' \in g(v) \\
& ~~~~~~~~ if ~ y \in \cup g^{-1}(g(v))^{\mathsf{c}}, ~ then ~ y' \notin g(v) \\
\Leftrightarrow & ~~~~ y \in N(y') \\
\end{aligned}
連続開写像と開集合系の交叉関係
$g$ により導出される $N'(y)$ と、連続開写像との関係を述べる。
命題1
\begin{aligned}
& \langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
\\
f:X \rightarrow X' \\
\exists g: & O \rightarrow O' ; surjection, \\
& \forall v \in O, f(v) = g(v) \\
& and ~ \forall y \in X, f(y) \in N'(y) \\
\Leftrightarrow & f: open~and~continuous, surjective~mapping \\
\end{aligned}
この命題1が意味しているのは、2つの位相空間における開集合系を対応づける写像$g$ に即して写像 $f$ を構築する際に、$f(y) \in N(y)$ を満たすように($f$ による移り先が、開集合系の交叉関係を崩さないようにマッピングすることで)、連続開写像にすることができるということである。
言い方を変えると、連続開写像とは、写像元と写像先の間の開集合系の交叉関係を保つ写像(移り先に模倣・再構築できる写像)と言える、ということでもある。
以下、当命題を証明していく。
開集合系の交叉関係が作る写像
補題1-1
\begin{aligned}
& \langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
\\
g: &O \rightarrow \mathcal{P}(X'); ~a~mapping~where~\mathcal{P}(X')~is~the~power~set~of~X' \\
\\
f: &X \rightarrow X' which \\
& \forall v \in O, f(v) = g(v) \\
& \forall y \in X, f(y) \in N'(y) \\
\Rightarrow & \forall v \in O, f^{-1}(f(v)) = \cup g^{-1}(g(v))
\end{aligned}
証明
\begin{aligned}
&\forall v \in O ~に対して示す \\
& まずは、\cup g^{-1}(g(v)) \subseteq f^{-1}(f(v)) ~について \\
\\
& \forall u \in g^{-1}(g(v)), \\
& g(u) = g(v) \\
& \therefore f(u) = f(v) \\
& ここで、~\forall x \in u, f(x) \in f(u) = f(v) であることに注目すると、\\
& f(x) \in f(v) \\
& つまり、~ x \in f^{-1}(f(v)) であることから \\
& u \subseteq f^{-1}(f(v)) \\
& \therefore \cup \{u \in O | u \in g^{-1}(g(v))\} \subseteq f^{-1}(f(v)) \\
& \cup g^{-1}(g(v)) \subseteq f^{-1}(f(v)) \\
\end{aligned}
次に、
\begin{aligned}
& f^{-1}(f(v)) \subseteq \cup g^{-1}(g(v)) ~について \\
\\
& \forall y \in f^{-1}(f(v)) (\subseteq X), \\
& f(y) \in N'(y) (\because 補題の条件) \\
& ここで、~ N'(y) := \underset{v: ~ y \in \cup g^{-1}(g(v))}{\bigcap} g(v) \cap \underset{v: ~ y \notin \cup g^{-1}(g(v))}{\bigcap} g(v)^{\mathsf{c}} ~である \\
& ここで、 y \notin \cup g^{-1}(g(v)) = \cup \{u \in O|g(u) = g(v) \}, とすると \\
& ~~~~~~~~ f(y) \in g(v)^{\mathsf{c}} ~~~~ (\because f(y) \in N'(y)) \\
& ~~~~~~~~ \therefore f(y) \in f(v)^{\mathsf{c}} ~~~~ (\because g(v) = f(v)) \\
& ~~~~~~~~ \therefore y \in f^{-1}(f(v)^{\mathsf{c}}) \\
& ~~~~~~~~ \therefore y \in f^{-1}(f(v))^{\mathsf{c}} \\
& ~~~~~~~~ \therefore y \notin f^{-1}(f(v)) \\
& \therefore y \notin \cup g^{-1}(g(v)) \Rightarrow y \notin f^{-1}(f(v)) \\
& \therefore y \in f^{-1}(f(v)) \Rightarrow y \in \cup g^{-1}(g(v)) \\
& \therefore y \in \cup g^{-1}(g(v)) ~~~~ (\because y \in f^{-1}(f(v))) \\
& f^{-1}(f(v)) \subseteq \cup g^{-1}(g(v)) \\
以上により、& \forall v \in O, f^{-1}(f(v)) = \cup g^{-1}(g(v)) \\
\end{aligned}
この補題が意味しているのは、開集合系に対する $f$ の像が $g$ により与えられ(制限され)、$f(y) \in N'(y)$ を満たす(y を含む像と含まない像の交叉関係が $f$ で移しても保存される)なら、$f^{-1}$ が $g^{-1}$ により制限されることを意味する。
系1-2
上記補題により、以下を導ける。
\begin{aligned}
& \langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
\\
g: &O \rightarrow O'; surjection ~~~~ (given) \\
\\
f: &X \rightarrow X' which \\
& \forall v \in O, f(v) = g(v) \\
& \forall y \in X, f(y) \in N'(y) \\
\Rightarrow & f: continuous \\
\end{aligned}
証明
\begin{aligned}
\forall v' & \in O', \\
\exists v & \in O; g(v) = v' ~~~~ (\because g: surjection) \\
& f^{-1}(v') \\
& = f^{-1}(g(v)) \\
& = f^{-1}(f(v)) \\
& = \cup g^{-1}((g(v)) ~~~~ (補題より) \\
& \in O ~~~~ (\because g: O \rightarrow O', ~and~O: closed~with~\cup) \\
\therefore \forall v' & \in O', f^{-1}(v') \in O \\
\therefore f: & continuous
\end{aligned}
系1-3
さらに、上記系により、直ちに以下が導ける
\begin{aligned}
& \langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
\\
g: &O \rightarrow O'; surjection ~~~~ (given) \\
\\
f: &X \rightarrow X' which \\
& \forall v \in O, f(v) = g(v) \\
& \forall y \in X, f(y) \in N'(y) \\
\Rightarrow & f: open,~continuous~and~surjective \\
\end{aligned}
連続開写像が作る開集合系の交叉関係
次に、目的の命題の逆の関係を示していく。
補題2-1
\begin{aligned}
& \langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
\\
f: &X \rightarrow X'; open~and~continuous \\
\Rightarrow & \exists g: O \rightarrow O'; ~ \forall v \in O, g(v) = f(v) ~and~
\cup g^{-1}(g(v)) = f^{-1}(f(v)) \\
\end{aligned}
証明
$g$ を 次のように定義する
\begin{aligned}
\forall v \in O, g(v) := f(v) \\
by~ f: open, g(v) \in O' \\
so, ~ g: O \rightarrow O' \\
\end{aligned}
この $g$ に対して、$\cup g^{-1}(g(v)) = f^{-1}(f(v))$ であることを示す
$\forall v \in O$ に対して、
まずは、$\cup g^{-1}(g(v)) \subseteq f^{-1}(f(v))$ であることを示す
\begin{aligned}
\forall x \in \cup g^{-1}(g(v)) & = \cup \{u \in O | g(u) = g(v) \} \\
\exists u & \in O; x \in u ~and~ g(u) = g(v) \\
f(x) & \in f(u) \\
f(x) & \in f(v) ~~~~ (\because f(u) = g(u) = g(v) = f(v)) \\
\therefore x & \in f^{-1}(f(v)) \\
\therefore \cup g^{-1}(g(v)) & \subseteq f^{-1}(f(v)) \\
\end{aligned}
次に、$f^{-1}(f(v)) \subseteq \cup g^{-1}(g(v))$ を示す
\begin{aligned}
\forall x \in f^{-1}(f(v)), \\
f(v) & \in O' ~~~~ (v \in O \& f: open) \\
f^{-1}(f(v)) & \in O ~~~~ (f: continuous) \\
\therefore \exists u & \in O; u = f^{-1}(f(v)) \\
\therefore x & \in u ~and~ f(u) = f(v) \\
\therefore x & \in u ~and~ g(u) = g(v) \\
\therefore x & \in u ~and~ u \in g^{-1}(g(v)) \\
\therefore x & \in u ~and~ u \subseteq \cup g^{-1}(g(v)) \\
\therefore x & \in \cup g^{-1}(g(v)) \\
\therefore f^{-1}(f(v)) & \subseteq \cup g^{-1}(g(v)) \\
\end{aligned}
以上により、$\cup g^{-1}(g(v)) = f^{-1}(f(v))$
補題2-2
\begin{aligned}
& \langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
\\
f: &X \rightarrow X' \\
\Rightarrow & \forall y \in X, f(y) \in N'_f(y)
\end{aligned}
証明
$\forall y \in X$ に対して示す
\begin{aligned}
\forall v \in O; y & \in f^{-1}(f(v)), \\
f(y) & \in f(v) \\
f(y) \in \cap & \{f(v) \in \mathcal{P}(X) | v \in O ~and~ y \in f^{-1}(f(v)) \} \\
f(y) & \in \underset{v: ~ y \in f^{-1}(f(v))}{\bigcap} f(v) \} \\
\\
一方、\\
\forall v \in O; y & \notin f^{-1}(f(v)), \\
y & \in f^{-1}(f(v))^{\mathsf{c}} \\
y & \in f^{-1}(f(v)^{\mathsf{c}}) \\
f(y) & \in f(v)^{\mathsf{c}} \\
f(y) \in \cap & \{f(v)^{\mathsf{c}} \in \mathcal{P}(X') | v \in O ~and~ y \notin f^{-1}(f(v)) \} \\
f(y) & \in \underset{v: ~ y \notin f^{-1}(f(v))}{\bigcap} f(v)^{\mathsf{c}} \\
\\
\therefore f(y) \in & \underset{v: ~ y \in f^{-1}(f(v))}{\bigcap} f(v) \cap \underset{v: ~ y \notin f^{-1}(f(v))}{\bigcap} f(v)^{\mathsf{c}} \\
\therefore f(y) \in & N'_f(y) \\
\end{aligned}
系2-3
\begin{aligned}
& \langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
\\
f: &X \rightarrow X'; ~open, ~and~ continuous \\
\Rightarrow \exists g: & O \rightarrow O'; \\
& ~ \forall v \in O, g(v) = f(v), \\
& ~and~ \forall y \in X, f(y) \in N'(y) \\
\end{aligned}
証明
補題2-1 より、
\begin{aligned}
\exists g: O \rightarrow O'; ~ \forall v \in O, g(v) = f(v) ~and~
\cup g^{-1}(g(v)) = f^{-1}(f(v)) \\
\end{aligned}
補題2-2 より、
\begin{aligned}
\forall y \in X, f(y) & \in N'_f(y) \\
\therefore \forall y \in X, f(y) & \in N'(y) ~~~~ (\because g(v) = f(v), \cup g^{-1}(g(v)) = f^{-1}(f(v))) \\
\end{aligned}
以上から、
\begin{aligned}
\exists g: & O \rightarrow O'; \\
& ~ \forall v \in O, g(v) = f(v), \\
& ~and~ \forall y \in X, f(y) \in N'(y) \\
\end{aligned}
命題1 の証明
系1-3, 系2-3 より、命題1 が示される
連続写像と開集合系の交叉関係
定理
命題1 を使うと、以下の定理が導ける
\begin{aligned}
& \langle X, O \rangle, \langle X', O' \rangle: topological~spaces \\
f: &X \rightarrow X'; a~map \\
\\
f: &X \rightarrow X'; ~continuous ~~ from \langle X, O \rangle ~to~\langle X', O' \rangle \\
\Leftrightarrow \exists O_f & \subseteq O; \\
& \exists g: O_f \rightarrow O'_f; surjective \\
& ~~~~~~~~ where ~ O'_f := \{v' \cap f(X) \in \mathcal{P}(X) | v' \in O' \} \\
& ~ \forall v \in O_f, g(v) = f(v), \\
& ~and~ \forall y \in X, f(y) \in N'(y) \\
\end{aligned}
この定理が主張するのは、連続写像とは、移り元の位相空間上の部分開集合系$O_f (\subseteq O)$から移り先の開集合系$O'$を $f$ の像で制限した部分位相空間$O'_f$において($f$ を連続開写像にする$O_f, O'_f$ において、とも言い換えられる)、各点$y \in X$ に関する開集合系$O_f$の交叉関係と$f$ の移り先でも同じ交叉関係を持つ($f(y) \in N'(y)$) ということを意味している
導出のヒント
\begin{aligned}
O_f & := \{f^{-1}(v') \in \mathcal{P}(X) | v' \in O' \} \subseteq O \\
g(v) & := f(v) \\
\end{aligned}
として、命題1 を使う
※ 気が向いたら、ちゃんと証明記載します・・
まとめ
- 連続開写像と開集合系の交叉関係の同値性を示し、連続写像の同値条件を新たに導出した
- 別の見方をすると、開集合系の交叉集合$N'(y)$、$N(y')$ の濃度は本質的ではない
- つまり、空集合か否かという点だけが重要である
- 極端な例としては、$N'(y)$ を1点集合となるような位相空間$\langle X', O' \rangle$を選出してもよい、ということである
- 特に、無限集合上の有限個の開集合系であれば、有限集合上の開集合系上に移して議論してもよい、ということである。
- これらのことは、位相モデル上の同値関係との関わりを示すことでより明確になる
- この後の展開としては、これを様相論理体系S4に対する意味論・位相モデルに拡張する
- つまり、様相論理においての論理的同値関係(論理的に意味が同じ)であることと開集合系の交叉関係との関わりについて導出する
- 導出済なので、また気が向いた時に・・
- これらの交叉関係とグラフ構造上の関係(束構造との関係)についても整理してみたいところ
- 開集合系上の写像 $g$ を導入したのは、もともと束構造と対応づけしたかった、とも言える
- 実際、修士論文では、有限開集合系上への束準同型写像として用いた
- 当時は、開集合系の濃度を有限と仮定しないと示せなかった ・・・