【キカガク流】人工知能・機械学習 脱ブラックボックス講座 - 初級編 -で学べること
この講座で学べることは以下の4つとなっています。
1.微分
2.単回帰分析
3.python速習
4.単回帰分析の実装
私の場合は特に1の微分について学びたいというモチベーションからこの講座を受講しました。
微分は、機械学習だけでなく深層学習を学ぶ上でも必要不可欠な要素です。
微分に関する専門書は多くありますが、数学から長らく遠ざかっていた身としてはなかなか厳しいものがありました。
本講座の微分の内容は機械学習に必要な部分にのみ焦点を当てつつ専門用語や計算方法もしっかりと解説しているので比較的すんなりと理解することができました。
1で微分をしっかりと理解した後で単回帰分析の実装を行ってみるとこれまで漠然としか理解できていなかった部分も
ちゃんと理解ができるようになりました。
udemyの各講座には30日間の返金保証があるので仮に自分に合わなかったとしても返金してもらうことができます。
理解できるか不安という方もで安心して受講できると思います。
【キカガク流】人工知能・機械学習 脱ブラックボックス講座 - 初級編 -
URL:https://www.udemy.com/kikagaku_blackbox_1/
参考になる資料
本講座単体でももちろんきちんと理解を深めることはできますが、以下の3つを追加の資料として利用しました。
1.メディカルAI専門コース オンライン講義資料
本講座の講師でもある株式会社キカガクの吉崎さんも作成に作成に加わっており講座の内容を補完するのにベストな資料だと思います。
2.ゼロから作るDeep Learning――Pythonで学ぶディープラーニングの理論と実装
オライリーから出版されている書籍です。
タイトルの通りライブラリを使わずにpythonとnumpyを使ってディープラーニングを実装していく書籍です。
この書籍に中でも微分について触れられています。
講座の中では微分を手計算で解いていきます。本書にはpythonでの実装する方法が解説されており、
実際に実装してグラフとしてプロットしてみると一層理解を深めることができると思います。
3.人工知能プログラミングのための数学がわかる本
機械学習などで使われる数学を学ぶためにはベストな1冊だと思います。
私も機械学習で使う数学を勉強したいと思って一番最初に手にしたのがこの本でした。
卒業以来久しぶりに数学に触れる人や数学に苦手意識のある方には少し難しい内容かもしれません。
微分を理解するためにやってみたこと
【キカガク流】人工知能・機械学習 脱ブラックボックス講座 - 初級編 -と上記でご紹介した資料を使って勉強すれば微分をきちんと理解することができます。
おすすめの勉強方法は、講座や資料の内容がある程度理解できるようになったら実際にpythonで微分を実装してみることです。
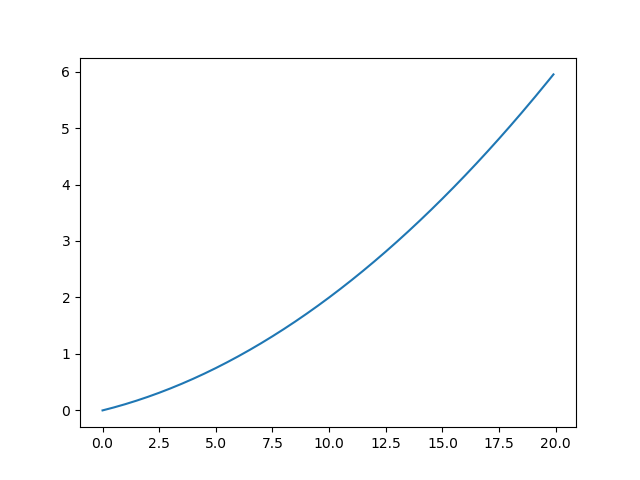
例えば、下記の関数とその微分を求める関数をpythonで実装してみます。
y = 0.01{x^2} + 0.1{x}
def func1(x):
return 0.01 * x**2 + 0.1 * x
実装できたらmatplotlibでグラフとしてプロットしてみると視覚的に確認できるのでおすすめです。
import numpy as np
import matplotlib.pylab as plt
x = np.arange(0.0, 20.0, 0.1) # 0から20まで、0.1刻みのx配列
y = func1(x)
plt.plot(x, y)
plt.show()
微分のもっとも単純な実装は以下です。
def num_diff(f, x):
h = 10e-50
return (f(x+h)-f(x)) / h
ただ上記の実装では丸め誤差によりhが0になってしまうのでそれを防ぐために下記のように変更します。
def num_diff(f, x):
h = 1e-4
return (f(x+h)-f(x)) / h
ただしもう1点問題があります。
x=5としてnum_diffで計算すると
>>> num_diff(func1, 5)
0.20000099999917254
となります。
実際の計算結果は0.2であるため誤差が生じていることが確認できます。
これは関数f(x)の差分において誤差が生じているためです。
それを解消するために下記のように変更します。
def num_diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h) #(x+h)と(x-h)でf(x)の差分を計算する
変更後の計算結果は下記のようになります。
完全に一致してはいませんが誤差が限りなく小さくなっていることがわかります。
>>> num_diff(func1, 5)
0.1999999999990898
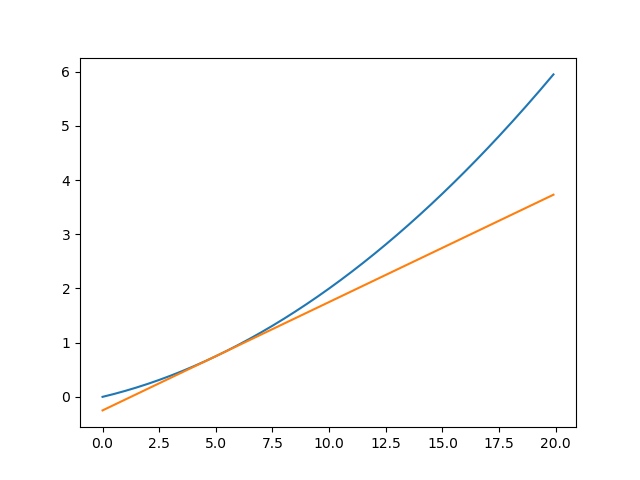
実装でき計算結果が正しいことが確認できたらグラフにプロットしてみると結果が正しいことが視覚的に理解できるのでおすすめです。
まとめ
数学が苦手な方、久しぶりに数学を学ぶ方にとって【キカガク流】人工知能・機械学習 脱ブラックボックス講座 - 初級編 -は最適な教材だと思います。
微分は公式が多く出てくるので最初は難しく感じるかもしれませんがその意味さえ理解していれば計算自体は比較的簡単です。
機械学習等で微分を用いる際は計算自体はプログラムがやってくれます。
大事なのは「微分は何を求めるために使うのか?」ということをしっかり理解することです。