この記事はデータ構造とアルゴリズム Advent Calendar2018 4日目の記事です。
データ構造とアルゴリズムAdvnet Calendar2018は、
"データ構造とアルゴリズムに関する話題なら何でもOKです。
メジャーなものからマイナーなものまで様々なトピックを好きなように書きましょう!"
ということで、本日は今更!?かもしれませんが、最も基本的なアルゴリズムの一つである線形探索についてです。特に特殊なことは書いていないと思いますので、線形探索を既にご存知の方は読まなくても大丈夫です。記法は昨年度の文字列アルゴリズムAdvent Calendar 文字列の基本的な定義、表記法などを使用します。
線形探索は、数値の配列$S[1,n]$上に数値$x$があるかどうかを配列の長さ$n$に対して線形時間($O(n)$時間)で計算するアルゴリズムです。(配列に格納するデータとクエリのデータが一致するかどうかの判定に$O(s)$時間かかる場合、$O(sn)$時間になります。説明を簡単にするために、定数時間($O(s) = O(1)$)で数値同士が一致するかどうかを判定可能な範囲の自然数の数値の配列にしています。)線形探索を利用して、配列中にある最小値(最大値)や配列$S[1,n]$上の先行値(与えられた値$x$以下の$S$上の最大の数値)や後行値(与えられた値$x$以上の$S$上の最小のの数値)なども線形時間で計算することができます。線形探索は配列上の短い範囲の探索で二分探索 より実装上、高速になることもあり,簡潔データ構造のrank/select辞書の実装(rsdic、sdsl)などにも使われています。以下、アルゴリズムの説明になっています。
アルゴリズム
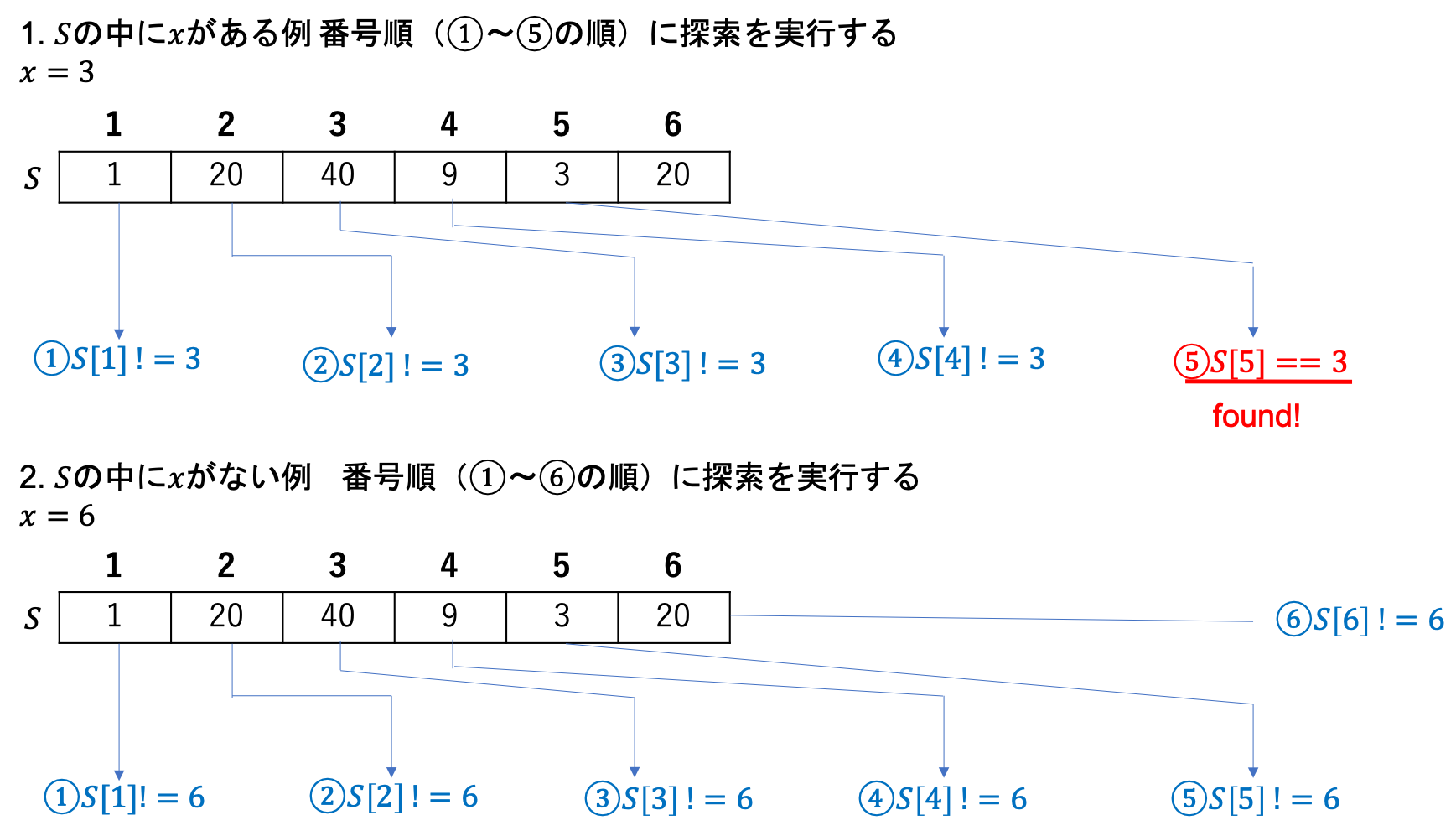
配列の先頭位置$S[1]$から順に$S[2]$、$S[3]$、...、$S[n]$まで各要素$S[i]$ ($1 \leq i \leq n$)が$S[i] == x$であるかどうかの確認を繰り返します。$S[i] == x$ならばその時点で探索を終了してtrueを返し、$S[1,n]$の全ての要素と不一致だった場合にfalseを返します。したがって、先頭の方で見つかれば高速に計算することが可能ですが、みつからない場合には配列の全ての要素と一致するかどうかを確認することになりますので、最悪計算時間は線形時間になります。$S$中で$x$が見つかる場合と見つからない場合の例と擬似コードを以下に示しておきます。
bool linearSearch(int *S,// 配列
int n, // 配列の長さ
int x) // クエリ
{
for(int i = 0; i < n; i++)
{
if(S[i] == x)
{
return true; // found x in S
}
}
return false; // not found x in S
}
以下、最小値、最大値、先行値、後行値を線形探索を利用して、計算する方法です。
線形探索で最小値(最大値)を見つける
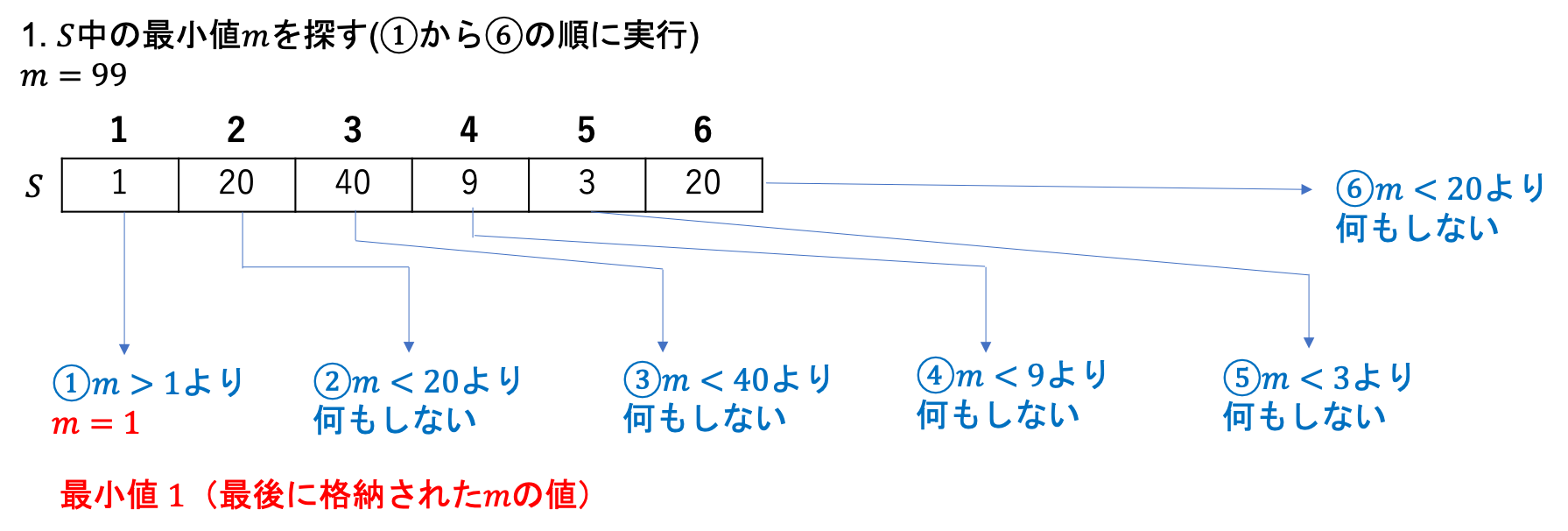
まず、最小値を線形探索を利用して、見つける方法について説明します。最小値を格納する変数$m$を用意します。$m$は$S$に格納する値の最大値に初期化しておきます。そして、$S[1]$、$S[2]$、...、$S[n]$の順に$m > S[i]$($1\leq i \leq n$)かどうかを確認していきます。$m > S[i]$($1\leq i \leq n$)の場合に$m$に$S[i]$を格納するという操作を繰り返し、最終的に$m$に格納されている値が最小値になります。$S$上の$n$個の要素全てに対して、1回の大小関係の判定と条件を満たす場合に$m$への格納の定数時間の定数回の操作を実行するので線形時間($O(n)$)になります。以下最小値の発見の例と擬似コードです。
int linearMinSearch(int *S,// 配列
int n) // 配列の長さ
{
int m = INT_MAX; //m:最小値を格納する変数、INT_MAX:intで表現可能な最大値2147483647
for(int i = 0; i < n; i++)
{
if(m > S[i])
{
m = S[i];
}
}
return m;
}
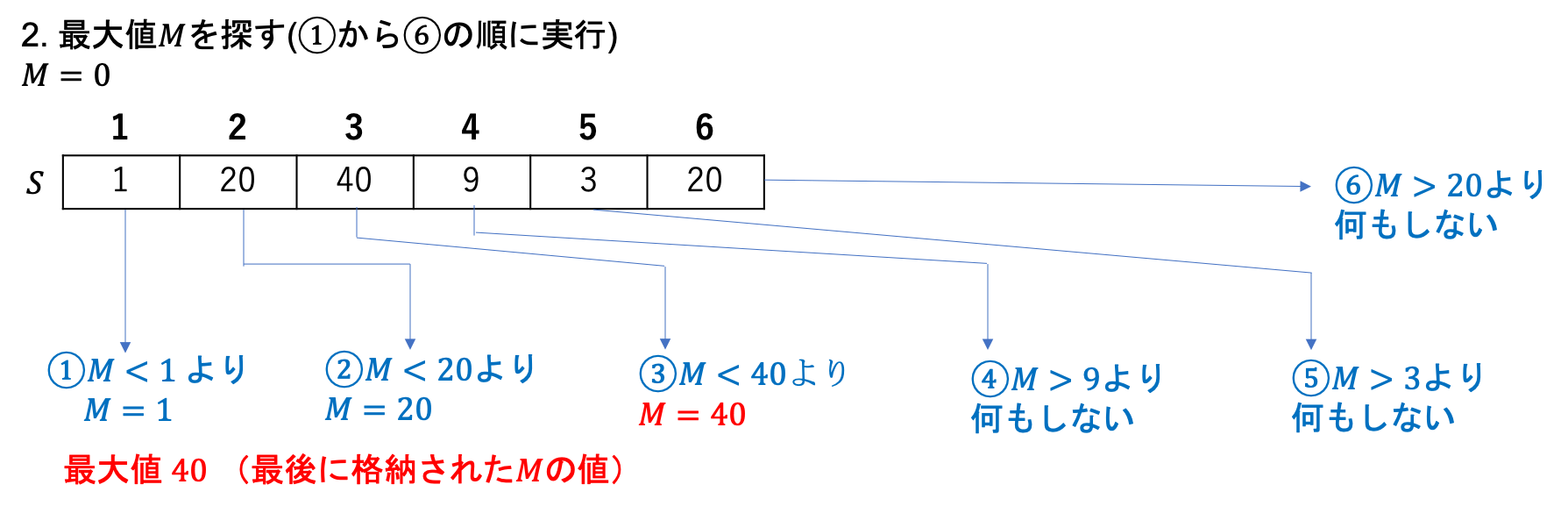
線形探索を利用して、最大値を見つけるのは最小値とほぼ同じです。最大値を格納する変数$M$を用意します。$M$は$S$に格納する値の最小値に初期化しておきます。そして、$S[1]$、$S[2]$、...、$S[n]$の順に$M < S[i]$($1\leq i \leq n$)かどうかを確認していきます。$M < S[i]$($1\leq i \leq n$)の場合に$M$に$S[i]$を格納するという操作を繰り返し、最終的に$M$に格納されている値が最大値になります。$S$上の$n$個の要素全てに対して、1回の大小関係の判定と条件を満たす場合に$m$への格納の定数時間の定数回の操作を実行するので線形時間($O(n)$)になります。以下最大値の発見の例と擬似コードです。
int linearMaxSearch(int *S,// 配列
int n) // 配列の長さ
{
int M = 0; // 最大値を格納する変数
for(int i = 0; i < n; i++)
{
if(M < S[i])
{
M = S[i];
}
}
return M;
}
線形探索で先行値(後行値)を見つける
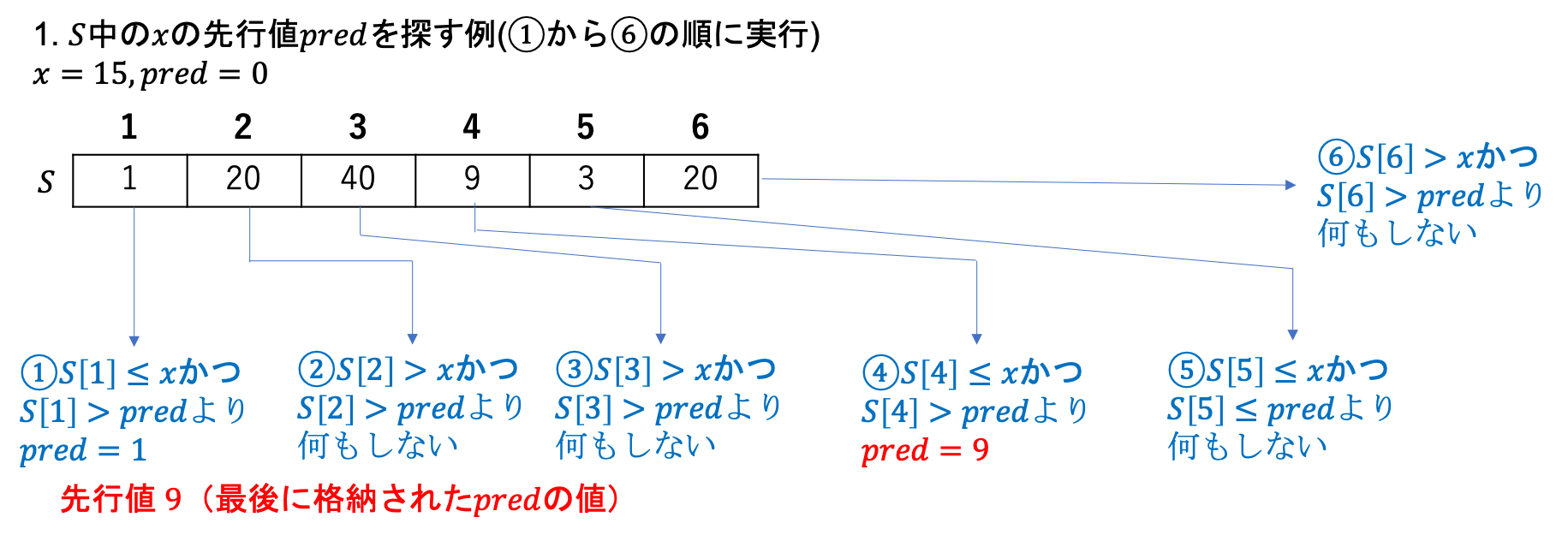
次は数値の配列$S$上の与えられた値$x$の先行値($x$以下の$S$上の最大の数値)を線形探索で計算する方法です。先行値を格納する変数$pred$を用意し、$S$に格納する最小値に初期化しておきます。そして、$S[1]$、$S[2]$、...、$S[n]$の順に$S[i] <= x$かつ$S[i] > pred$($1\leq i \leq n$)かどうかを確認していきます。$S[i] <= x$かつ$S[i] > pred$($1\leq i \leq n$)の場合に$pred$に$S[i]$を格納していき、最終的に$pred$に格納されている値が先行値になります。 $S$上の$n$個の要素全てに対して、2回の大小関係の判定と条件を満たす場合に$pred$への格納という定数時間の定数回の操作を実行するので線形時間($O(n)$)になります。以下、先行値の発見の例と擬似コードです。
bool linearPredecessorSearch(int *S,// 配列
int n, // 配列の長さ
int x) // クエリ
{
int pred = 0; // 先行値を格納する変数、配列に格納する最小値に初期化
for(int i = 0; i < n; i++)
{
if(S[i] <= x && S[i] > pred)
{
pred = S[i];
}
}
return pred;
}
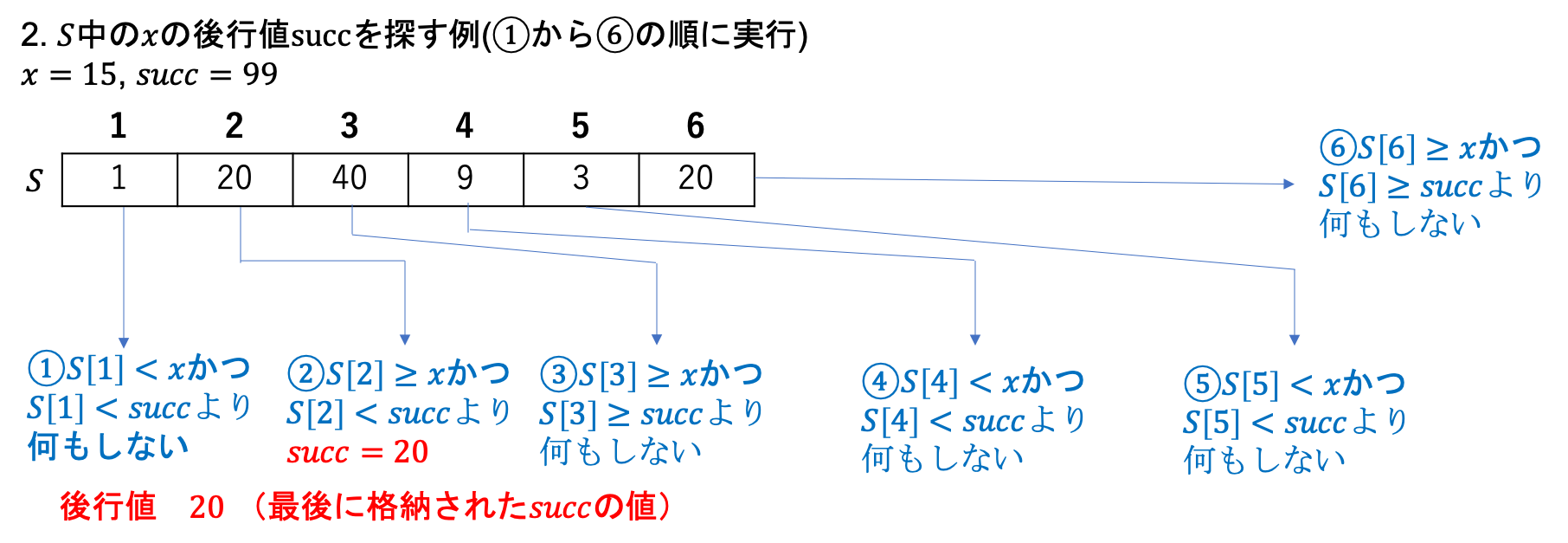
後行値(与えられた$x$以上の配列$S$上の最小の数値)の線形探索を利用した計算は先行値とほぼ同じです。後行値を格納する変数$succ$を用意し、$S$に格納する最大値に初期化しておきます。そして、$S[1]$、$S[2]$、...、$S[n]$の順に$S[i] >= x$かつ$S[i] < succ$($1\leq i \leq n$)かどうかを確認していきます。$S[i] >= x$かつ$S[i] < succ$($1\leq i \leq n$)の場合に$succ$に$S[i]$を格納していき、最終的に$succ$に格納されている値が後行値になります。 $S$上の$n$個の要素全てに対して、2回の大小関係の判定と条件を満たす場合に$succ$への格納と定数時間という定数回の操作を実行するので線形時間($O(n)$)になります。以下、後行値の発見の例と擬似コードです。
bool linearSuccessorSearch(int *S,// 配列
int n, // 配列の長さ
int x) // クエリ
{
int succ = INT_MAX; // 後行値を格納する変数、配列に格納する最大値に初期化
for(int i = 0; i < n; i++)
{
if(S[i] >= x && S[i] < succ)
{
succ = S[i];
}
}
return succ;
}
線形探索 vs 二分探索
線形探索と二分探索の実行時間を計測してみました。
ソースと結果を以下に載せておきます。
# include <iostream>
# include <vector>
# include <cstdint>
# include <iomanip>
# include <random>
# include <chrono>
# include <algorithm>
using namespace std;
inline bool linearSearch(std::vector<int> &S,// 配列
int x) //クエリ
{
for(int i = 0;
i < S.size();
++i)
{
if(S[i] == x)
{
return true; // found x in S
}
}
return false; // not found x in S
}
inline bool binarySearch(std::vector<int> &S,
int begin,
int end,
int x)
{
int mid = 0;
while (begin <= end)
{
mid = (begin + end) >> 1;
if(S[mid] == x)
{
return true;
}
else if(x > S[mid])
{
begin = mid + 1;
}
else if(x < S[mid])
{
end = mid - 1;
}
}
return false;
}
int main(void)
{
vector<int> S;
vector<int> random_;
for(int s_len = 2;
s_len <= (INT32_MAX >> 1);
s_len <<= 1)
{
cout << "vector length: " << s_len << endl;
S.resize(s_len);
cout << S.size() << endl;
for(int i = 0;
i < s_len;
++i)
{
S[i] = i;
}
int sum = 0;
int loop = 10000;
auto start = std::chrono::system_clock::now();
for(int ind1 = 0;
ind1 < loop;
++ind1)
{
for(int ind2 = 0;
ind2 < s_len;
++ind2)
{
//最適化するとlinearSearch関数が意味のない関数として消えるので、
// sumを入れています。
sum += linearSearch(S,
S[ind2]);
}
}
auto end = std::chrono::system_clock::now();
auto diff = end - start;
std::cout << "debug sum: " << sum << endl;
std::cout << "linear search time = "
<< std::chrono::duration_cast<std::chrono::nanoseconds>(diff).count()/loop/s_len
<< " nano sec."
<< std::endl;
int s_size = S.size() - 1;
auto start2 = std::chrono::system_clock::now();
for(int ind3 = 0;
ind3 < loop;
++ind3)
{
for(int ind4 = 0;
ind4 < s_len;
++ind4)
{
sum += binarySearch(S,
0,
S.size() - 1,
S[ind4]);
}
}
auto end2 = std::chrono::system_clock::now();
auto diff2 = end2 - start2;
std::cout << "debug sum: " << sum << endl;
std::cout << "binary search time = "
<< std::chrono::duration_cast<std::chrono::nanoseconds>(diff2).count()/loop/s_len
<< " nano sec."
<< std::endl;
}
return 1;
}
実行結果
実験環境:Intel(R) Xeon(R) CPU E7- 8837 @ 2.67GHz, 1TB memory, CentOS
$ g++ -std=c++1z -Ofast linearvsbinarysearch.cpp
$ ./a.out
vector length: 2
2
debug sum: 20000
linear search time = 9 nano sec.
debug sum: 40000
binary search time = 8 nano sec.
vector length: 4
4
debug sum: 40000
linear search time = 11 nano sec.
debug sum: 80000
binary search time = 10 nano sec.
vector length: 8
8
debug sum: 80000
linear search time = 17 nano sec.
debug sum: 160000
binary search time = 13 nano sec.
vector length: 16
16
debug sum: 160000
linear search time = 26 nano sec.
debug sum: 320000
binary search time = 5 nano sec.
vector length: 32
32
debug sum: 320000
linear search time = 25 nano sec.
debug sum: 640000
binary search time = 14 nano sec.
vector length: 64
64
debug sum: 640000
linear search time = 38 nano sec.
debug sum: 1280000
binary search time = 28 nano sec.
vector length: 128
128
debug sum: 1280000
linear search time = 61 nano sec.
debug sum: 2560000
binary search time = 41 nano sec.
vector length: 256
256
debug sum: 2560000
linear search time = 106 nano sec.
debug sum: 5120000
binary search time = 41 nano sec.
vector length: 512
512
debug sum: 5120000
linear search time = 197 nano sec.
debug sum: 10240000
binary search time = 41 nano sec.
vector length: 1024
1024
debug sum: 10240000
linear search time = 381 nano sec.
debug sum: 20480000
binary search time = 42 nano sec.
短い時は線形探索の方が高速なのかと思っていましたが、長さ8くらいまでは線形探索と二分探索でほぼ同性能で、それより長い場合は二分探索が良いという結果になりました。
なんとなく、短い時は線形探索、長い時は二分探索と組み合わせれば速くなるかなと思って、二つを組み合わせてみました。長さが8より大なら二分探索で、長さ8以下になったら線形探索に切り替えてみました。(この切り替えは既にやっている人もいると思います。)
inline bool HybridSearch(std::vector<int> &S,
int begin,
int end,
int x)
{
int mid = 0;
while ((begin + 8) <= end)
{
mid = (begin + end) >> 1;
if(S[mid] == x)
{
return true;
}
else if(x > S[mid])
{
begin = mid + 1;
}
else if(x < S[mid])
{
end = mid - 1;
}
}
for(;
begin <= end;
++begin)
{
if(S[begin] == x)
{
return true;
}
}
return false;
}
実行結果
$ g++ -std=c++1z -Ofast linearvsbinaryvshybridsearch.cpp
$ ./a.out
vector length: 2
2
debug sum: 20000
linear search time = 9 nano sec.
debug sum: 40000
binary search time = 9 nano sec.
debug sum: 60000
hybrid search time = 12 nano sec.
vector length: 4
4
debug sum: 40000
linear search time = 10 nano sec.
debug sum: 80000
binary search time = 10 nano sec.
debug sum: 120000
hybrid search time = 15 nano sec.
vector length: 8
8
debug sum: 80000
linear search time = 14 nano sec.
debug sum: 160000
binary search time = 12 nano sec.
debug sum: 240000
hybrid search time = 18 nano sec.
vector length: 16
16
debug sum: 160000
linear search time = 19 nano sec.
debug sum: 320000
binary search time = 5 nano sec.
debug sum: 480000
hybrid search time = 7 nano sec.
vector length: 32
32
debug sum: 320000
linear search time = 24 nano sec.
debug sum: 640000
binary search time = 24 nano sec.
debug sum: 960000
hybrid search time = 17 nano sec.
vector length: 64
64
debug sum: 640000
linear search time = 37 nano sec.
debug sum: 1280000
binary search time = 32 nano sec.
debug sum: 1920000
hybrid search time = 17 nano sec.
vector length: 128
128
debug sum: 1280000
linear search time = 57 nano sec.
debug sum: 2560000
binary search time = 42 nano sec.
debug sum: 3840000
hybrid search time = 26 nano sec.
vector length: 256
256
debug sum: 2560000
linear search time = 102 nano sec.
debug sum: 5120000
binary search time = 40 nano sec.
debug sum: 7680000
hybrid search time = 33 nano sec.
vector length: 512
512
debug sum: 5120000
linear search time = 194 nano sec.
debug sum: 10240000
binary search time = 40 nano sec.
debug sum: 15360000
hybrid search time = 36 nano sec.
vector length: 1024
1024
debug sum: 10240000
linear search time = 378 nano sec.
debug sum: 20480000
binary search time = 42 nano sec.
debug sum: 30720000
hybrid search time = 39 nano sec.
短い時の性能はほとんど二分探索と変わりません(若干悪くなってます)が、
長い時の性能が二分探索より若干高速になるという結果になりました。
おわりに
という訳で、最も基本的なアルゴリズムの一つである線形探索についてでした。
追記(ソースコード修正&実験取り直し)
linearSearchの仕様をbinarySearchと揃えて、試行回数を増やして、時間をdoubleにcastすることで小数点以下を表示しました。その結果、長さ8までは線形探索が高速で、長さ8より大の場合は二分探索が高速になりました。
# include <iostream>
# include <vector>
# include <cstdint>
# include <iomanip>
# include <random>
# include <chrono>
# include <algorithm>
using namespace std;
inline bool linearSearch(std::vector<int> &S,// 配列
int begin,
int end,
int x) //クエリ
{
for(;
begin <= end;
++begin)
{
if(S[begin] == x)
{
return true; // found x in S
}
}
return false; // not found x in S
}
int midbs = 0;
inline bool binarySearch(std::vector<int> &S,
int begin,
int end,
int x)
{
while (begin <= end)
{
midbs = (begin + end) >> 1;
if(S[midbs] == x)
{
return true;
}
else if(x > S[midbs])
{
begin = midbs + 1;
}
else if(x < S[midbs])
{
end = midbs - 1;
}
}
return false;
}
int midhs = 0;
inline bool HybridSearch(std::vector<int> &S,
int begin,
int end,
int x)
{
while ((begin + 8) <= end)
{
midhs = (begin + end) >> 1;
if(S[midhs] == x)
{
return true;
}
else if(x > S[midhs])
{
begin = midhs + 1;
}
else if(x < S[midhs])
{
end = midhs - 1;
}
}
for(;
begin <= end;
++begin)
{
if(S[begin] == x)
{
return true;
}
}
return false;
}
int main(void)
{
vector<int> S;
vector<int> random_;
for(int s_len = 2;
s_len <= (INT32_MAX >> 1);
s_len += 1)
{
cout << "vector length: " << s_len << endl;
S.resize(s_len);
cout << S.size() << endl;
for(int i = 0;
i < s_len;
++i)
{
S[i] = i;
}
int sum = 0;
int loop = 100000000;
int s_size = S.size() - 1;
auto start = std::chrono::system_clock::now();
for(int ind1 = 0;
ind1 < loop;
++ind1)
{
for(int ind2 = 0;
ind2 < s_len;
++ind2)
{
sum += linearSearch(S,
0,
s_size,
S[ind2]);
}
}
auto end = std::chrono::system_clock::now();
auto diff = end - start;
std::cout << "debug sum: " << sum << endl;
std::cout << "linear search time = "
<< (double)std::chrono::duration_cast<std::chrono::nanoseconds>(diff).count()/loop/s_len
<< " nano sec."
<< std::endl;
auto start2 = std::chrono::system_clock::now();
for(int ind3 = 0;
ind3 < loop;
++ind3)
{
for(int ind4 = 0;
ind4 < s_len;
++ind4)
{
sum += binarySearch(S,
0,
s_size,
S[ind4]);
}
}
auto end2 = std::chrono::system_clock::now();
auto diff2 = end2 - start2;
std::cout << "debug sum: " << sum << endl;
std::cout << "binary search time = "
<< (double)std::chrono::duration_cast<std::chrono::nanoseconds>(diff2).count()/loop/s_len
<< " nano sec."
<< std::endl;
auto start3 = std::chrono::system_clock::now();
for(int ind5 = 0;
ind5 < loop;
++ind5)
{
for(int ind6 = 0;
ind6 < s_len;
++ind6)
{
sum += HybridSearch(S,
0,
s_size,
S[ind6]);
}
}
auto end3 = std::chrono::system_clock::now();
auto diff3 = end3 - start3;
std::cout << "debug sum: " << sum << endl;
std::cout << "hybrid search time = "
<< (double)std::chrono::duration_cast<std::chrono::nanoseconds>(diff3).count()/loop/s_len
<< " nano sec."
<< std::endl;
}
return 1;
}
実行結果
linear vs binary vs hybrid (長さ:2~12)
vector length: 2
2
debug sum: 200000000
linear search time = 3.01528 nano sec.
debug sum: 400000000
binary search time = 3.51006 nano sec.
debug sum: 600000000
hybrid search time = 4.24142 nano sec.
vector length: 3
3
debug sum: 300000000
linear search time = 3.11395 nano sec.
debug sum: 600000000
binary search time = 3.53334 nano sec.
debug sum: 900000000
hybrid search time = 4.55236 nano sec.
vector length: 4
4
debug sum: 400000000
linear search time = 3.50335 nano sec.
debug sum: 800000000
binary search time = 4.04189 nano sec.
debug sum: 1200000000
hybrid search time = 4.84968 nano sec.
vector length: 5
5
debug sum: 500000000
linear search time = 4.02389 nano sec.
debug sum: 1000000000
binary search time = 4.63648 nano sec.
debug sum: 1500000000
hybrid search time = 5.31693 nano sec.
vector length: 6
6
debug sum: 600000000
linear search time = 4.3108 nano sec.
debug sum: 1200000000
binary search time = 4.64633 nano sec.
debug sum: 1800000000
hybrid search time = 5.6282 nano sec.
vector length: 7
7
debug sum: 700000000
linear search time = 4.61885 nano sec.
debug sum: 1400000000
binary search time = 4.67972 nano sec.
debug sum: 2100000000
hybrid search time = 5.95372 nano sec.
vector length: 8
8
debug sum: 800000000
linear search time = 4.93938 nano sec.
debug sum: 1600000000
binary search time = 4.94 nano sec.
debug sum: -1894967296
hybrid search time = 7.53655 nano sec.
vector length: 9
9
debug sum: 900000000
linear search time = 5.26988 nano sec.
debug sum: 1800000000
binary search time = 5.04957 nano sec.
debug sum: -1594967296
hybrid search time = 5.34847 nano sec.
vector length: 10
10
debug sum: 1000000000
linear search time = 7.47456 nano sec.
debug sum: 2000000000
binary search time = 5.22055 nano sec.
debug sum: -1294967296
hybrid search time = 5.53281 nano sec.
vector length: 11
11
debug sum: 1100000000
linear search time = 9.27556 nano sec.
debug sum: -2094967296
binary search time = 5.31272 nano sec.
debug sum: -994967296
hybrid search time = 5.78016 nano sec.
vector length: 12
12
debug sum: 1200000000
linear search time = 10.7184 nano sec.
debug sum: -1894967296
binary search time = 5.29859 nano sec.
debug sum: -694967296
hybrid search time = 5.95774 nano sec.
binary vs hybrid (長さ16~64)
16
debug sum: 1600000000
binary search time = 5.43711 nano sec.
debug sum: -1094967296
hybrid search time = 7.27956 nano sec.
vector length: 32
32
debug sum: -1094967296
binary search time = 20.4471 nano sec.
debug sum: 2105032704
hybrid search time = 12.3521 nano sec.
vector length: 64
64
debug sum: 2105032704
binary search time = 31.9433 nano sec.
debug sum: -84901888
hybrid search time = 19.4563 nano sec.
さらにhybridSearchをチューニング!
int midhs = 0;
inline bool HybridSearch(std::vector<int> &S,
int begin,
int end,
int x)
{
if((end - begin) <= 8)
{
for(;
begin <= end;
++begin)
{
if(S[begin] == x)
{
return true;
}
}
}
while ((begin + 8) <= end)
{
midhs = (begin + end) >> 1;
if(S[midhs] == x)
{
return true;
}
else if(x > S[midhs])
{
begin = midhs + 1;
}
else if(x < S[midhs])
{
end = midhs - 1;
}
}
for(;
begin <= end;
++begin)
{
if(S[begin] == x)
{
return true;
}
}
return false;
}
実行結果 binary vs hybrid2
vector length: 2
2
debug sum: 200000000
binary search time = 3.63822 nano sec.
debug sum: 400000000
hybrid search time = 3.59466 nano sec.
vector length: 4
4
debug sum: 400000000
binary search time = 4.33695 nano sec.
debug sum: 800000000
hybrid search time = 3.54901 nano sec.
vector length: 8
8
debug sum: 800000000
binary search time = 5.25678 nano sec.
debug sum: 1600000000
hybrid search time = 3.9988 nano sec.
vector length: 16
16
debug sum: 1600000000
binary search time = 6.24843 nano sec.
debug sum: -1094967296
hybrid search time = 8.37897 nano sec.
vector length: 32
32
debug sum: -1094967296
binary search time = 13.2499 nano sec.
debug sum: 2105032704
hybrid search time = 14.0008 nano sec.
vector length: 64
64
debug sum: 2105032704
binary search time = 29.233 nano sec.
debug sum: -84901888
hybrid search time = 18.6899 nano sec.