この記事は BrainPad AdventCalendar 2017 6日目の記事です。
はじめに
業務でアンサンブル学習器を活用するにあたり、会社の読み会で読んでるあのオレンジの「アンサンブル法による機械学習」の中に出てきて面白かった完全ランダム木を活用した確率密度推定をご紹介します。
普段アンサンブル学習器は教師あり学習で活用することがほとんどでしたが、今回はある種教師なし学習的に使います。具体的には完全ランダム木をアンサンブルした学習器(以下、完全ランダム森)で、すべてのサンプルが一つずつ最終ノードに入るまで木を生い茂らせ、その深度を基にそのデータが生まれてくる確率密度を推定してやろうというものです。
完全ランダム木のアルゴリズム
ご存知の方も多いかと思いますが、決定木は木の各ノードにおいて何かしらの指標に基いて決定論的に特徴量とその分割点が選ばれますが、完全ランダム木はそれらが無作為に選ばれます。
Input: データセット $D$
Process:
- $N \leftarrow D$ に基いて木のノードを構築;m
- if 全てのインスタンスが同じクラスに含まれる場合 then return $N$;
- $F \leftarrow$ さらに分割可能な特徴の集合;
- if $F$ が空 then return $N$;
- $N.f \leftarrow$ランダムに$F$から選択された特徴;
- $N.p \leftarrow$ランダムに$N.p$に対して選択された分割点;
- $D_l \leftarrow N.p$ 以下の$N.f$の値を持つ$D$の部分集合;
- $D_r \leftarrow N.p$ 以下ではない$N.f$の値を持つ$D$の部分集合;
- $N_l \leftarrow D_l$で再帰的にノードを構築
10.$N_r \leftarrow D_r$で再帰的にノードを構築
11.return $N$
そして完全ランダム木をバギングしたものが完全ランダム森です。
完全ランダム森による確率密度推定
さて完全ランダム森については、ランダムフォレストなどに親しみがある方であれば理解は容易かと思います。しかしアンサンブル学習器を教師無し学習的に使って確率密度求めるというのはあまり馴染みのないアイデアではないでしょうか。
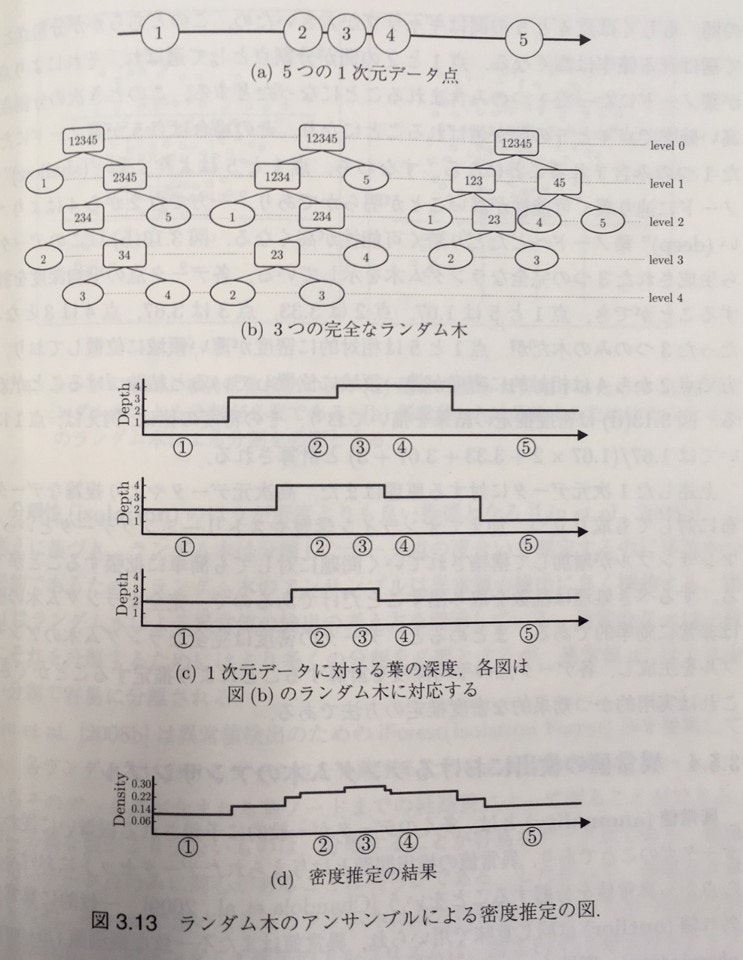
実際に、どのように完全ランダム森を使って確率密度推定を行うかを図示したものが下記になります。(アンサンブル法による機械学習p67 図3.13)
教師無し学習として完全ランダム森を活用するので、教師用データやクラス分けのための学習という概念は存在しません。構築される木において、それぞれのサンプルデータが最終ノードに落ちるまで気を生い茂らせ、それぞれのノードの深度を測ります。この木はランダムに分割点を作っているので、データの密度が低いところは容易に分割出来る=ノードの深度が浅くなる、データの密度が高いところは分割が難しい=ノードの深度が深くなります。そしてこの深度をアンサンブルし確率密度とするというものです。
上述の本では、
・高次元やより複雑なデータ分布にたいしても成り立つ
・オンライン学習や、ストリーミングデータといった、アンサンブルが増加して構築されていrく問題に対しても簡単に拡張することができる
ということがメリットとして記述され、「実用的かつ効果的な密度推定の方法である」、とされていました。
なんか良いことだらけのように見えますので、どんな感じで使えるのか試してみたいと思います。
Pythonで実装してみる
完全ランダム森はsklearnのExtraTreesにてモデルの引数にてmax_features=1を指定することで活用できます。密度推定をする過程で、それぞれのサンプルを最終ノードに一個ずつになるまで木を生やす必要があるので、それぞれのサンプルが別のクラスラベルを持っているクラス分類問題として解くのが良さそうです。
データを完全ランダム森に食わせた際の深度ですが、decision_path()というメソッドで木構造の中のどのノードを通ったかというのがトレースできるindicatorというものがsparse csr arrayにて返ってきます。通ったノード数すなわち深度という考え方で活用します。
詳細はsklearnのsklearn.ensemble.ExtraTreesClassifierを御覧ください。
from sklearn.ensemble import ExtraTreesClassifier
n_estimators = 1000
clf = ExtraTreesClassifier(n_estimators=n_estimators, max_features = 1, random_state=3655, n_jobs=8)
clf.fit(X,y)
indicator, n_nodes_ptr = clf.decision_path(X_grid)
mean_depth = np.sum(indicator.toarray(), axis=1)/float(n_estimators)
density = mean_depth/sum(mean_depth)
Python KDEパッケージとの比較
上記のようなアルゴリズムの特性を考えると比較すべきはカーネル密度推定(Kernel density estimation:KDE)のようなノンパラメトリックな推定方法だと考ます。Pythonとカーネル密度推定(KDE)について調べたまとめで、いい感じにまとめて下さってたので詳しいことは参照してもらった方が早そうです。
やってみたこと
ひとまず完全ランダム森密度推定のメリット云々の前にちゃんと挙動するかどうかを知りたかったので下記を試してみました。
・iris petal lengsh(cm)への密度推定が良さげかどうか
前述のばんくし氏のブログで使われているデータ。
・単峰性分布への密度推定が良さげかどうか
・多峰性分布への密度推定が良さげかどうか
・PythonKDEパッケージとの実行速度比較
iris petal lengthへの適用
他実装との比較ができるよう、前述のばんくし氏のブログと同様のデータセットを使用してみました。違いがあるとすると、念のためデータはこんな感じ。
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
from sklearn import datasets
# irisデータセットサンプル
iris = datasets.load_iris()
# pandas
data_pd = pd.DataFrame(data=iris["data"], columns=iris["feature_names"])
data_pd.head()
# irisの"petal length (cm)"カラムを利用する
# list
data_list = [x[3] for x in iris["data"]]
# np.array
data_np = np.array(data_list)
# x軸をGridするためのデータも生成
x_grid = np.linspace(0, max(data_list), num=150)
# データを正規化したヒストグラムを表示する用
weights = np.ones_like(data_list)/float(len(data_list))
# ExtraTreesでサンプル毎に違うノードに落とす過程が必要なのでそれぞれのサンプルに別のラベルを振る
y = range(data_np[:,None].shape[0])
このデータにて密度推定してみます。バンド幅を設定してやる必要のあるKDEと違いハイパーパラメーターはn_estimatorのみ、しかもこれは分布の形状には大きく影響及ぼさない(他に強いて挙げるならrandom seed)なので、楽っちゃ楽です。
# -*- coding: utf-8 -*-
from sklearn.neighbors import KernelDensity
import statsmodels.api as sm
from sklearn.ensemble import ExtraTreesClassifier
# sklearn KDE
# default
kde_model = KernelDensity(kernel='gaussian').fit(data_np[:, None])
score = kde_model.score_samples(x_grid[:, None])
# bw値を調整
bw01 = 0.1
kde_mode_bw01 = KernelDensity(bandwidth=bw01, kernel='gaussian').fit(data_np[:, None])
score_bw01 = kde_mode_bw01.score_samples(x_grid[:, None])
# bw値を調整
bw05 = 0.5
kde_mode_bw05 = KernelDensity(bandwidth=bw05, kernel='gaussian').fit(data_np[:, None])
score_bw05 = kde_mode_bw05.score_samples(x_grid[:, None])
# sklearn ExtraTree
n_estimators = 1000
y = range(data_np[:,None].shape[0])
clf = ExtraTreesClassifier(n_estimators=n_estimators, max_features = 1, random_state=3655, n_jobs=8)
clf.fit(data_np[:,None],y)
indicator, n_nodes_ptr = clf.decision_path(x_grid[:,None])
mean_depth = np.sum(indicator.toarray(), axis=1)/float(n_estimators)
density = mean_depth/sum(mean_depth)
plt.figure(figsize=(14,7))
plt.hist(data_list, alpha=0.3, bins=20, weights=weights)
plt.plot(x_grid, np.exp(score), label="default")
plt.plot(x_grid, np.exp(score_bw01), label="band width=0.1")
plt.plot(x_grid, np.exp(score_bw05), label="band width=0.5")
plt.plot(x_grid, density, label="ExtraTrees")
plt.legend()
plt.xlim([0, 2.5])
plt.ylim([0, 1.0])
plt.show()
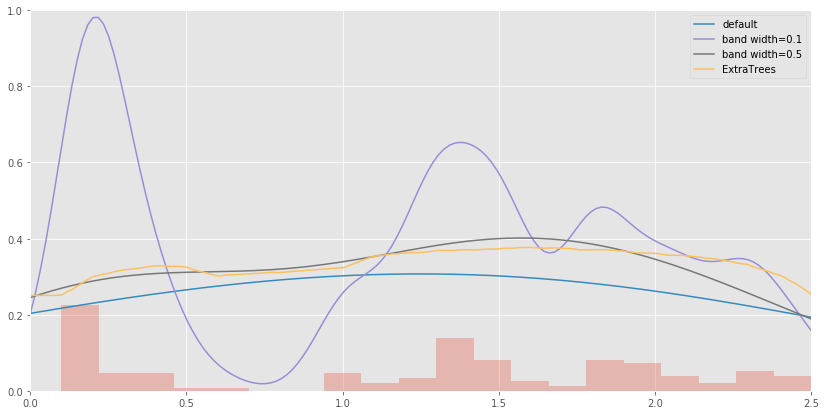
sklearn KDEでバンド幅を0.5に指定した時と似たような密度推定となっていますが、それ以上の細かい調整のようなものは出来ません。
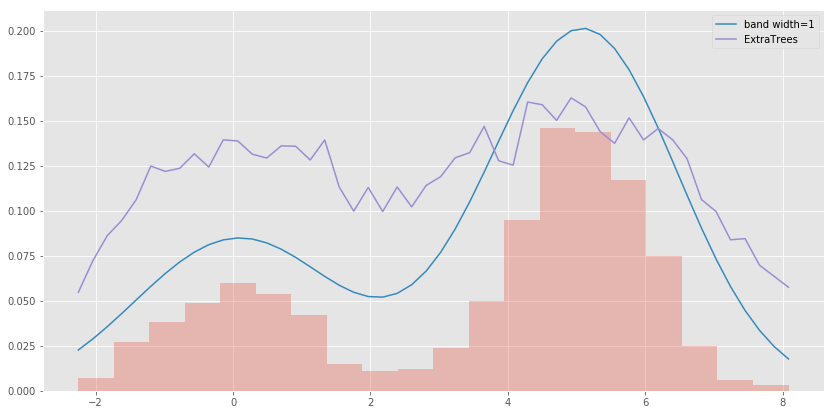
単峰性分布への密度推定が良さげかどうか
次に単純な単峰性を持った分布への密度推定をやってみます。完全にパラメトリックな推定の正解の話ではありますが、ひとまずアルゴリズムの挙動を見る目的で。
n = 1000
np.random.seed(3655)
data_np = np.random.normal(0, 1, n)
# x軸をGridするためのデータも生成
x_grid = np.linspace(min(data_np), max(data_np), num=50)
weights = np.ones_like(data_np)/float(len(data_np))
y = range(data_np[:,None].shape[0])
# sklearn KDE
# bw値を調整
bw = 1
kde_mode_bw = KernelDensity(bandwidth=bw, kernel='gaussian').fit(data_np[:, None])
score_bw = kde_mode_bw.score_samples(x_grid[:, None])
# sklearn ExtraTree
n_estimators = 1000
y = range(data_np[:,None].shape[0])
clf = ExtraTreesClassifier(n_estimators=n_estimators, max_features = 1, random_state=3655, n_jobs=-1)
clf.fit(data_np[:,None],y)
indicator, n_nodes_ptr = clf.decision_path(x_grid[:,None])
avg_depth = np.sum(indicator.toarray(), axis=1)/float(n_estimators)
mean_avg_depth = avg_depth/sum(avg_depth)
# 手元でスケール合わせてるの本当は良くない
plt.figure(figsize=(14,7))
plt.hist(data_np, alpha=0.3, bins=20, weights=weights)
plt.plot(x_grid, np.exp(score_bw)*0.7, label="band width=1")
plt.plot(x_grid, mean_avg_depth*6, label="ExtraTrees")
plt.legend()
plt.show()
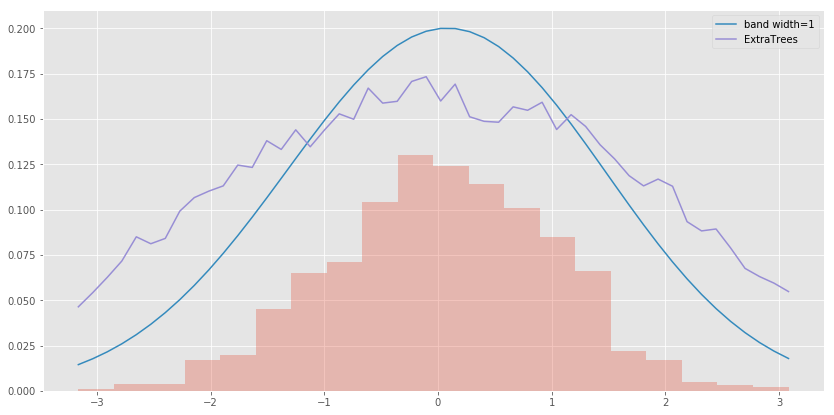
データは素直な正規分布から生成しているので、KDEが推定したような確率密度が真の分布に近いのですが、完全ランダム森はギザギザが残りますね。これはn_estimatorの数を増やしても変わりませんでした。
多峰性分布への密度推定が良さげかどうか
次に多峰性のあるデータについてです。
n = 1000
np.random.seed(3655)
data_np = np.random.normal(0, 1, n)
# x軸をGridするためのデータも生成
x_grid = np.linspace(min(data_np), max(data_np), num=50)
weights = np.ones_like(data_np)/float(len(data_np))
y = range(data_np[:,None].shape[0])
# sklearn KDE
# bw値を調整
bw = 1
kde_mode_bw = KernelDensity(bandwidth=bw, kernel='gaussian').fit(data_np[:, None])
score_bw = kde_mode_bw.score_samples(x_grid[:, None])
# sklearn ExtraTree
n_estimators = 1000
y = range(data_np[:,None].shape[0])
clf = ExtraTreesClassifier(n_estimators=n_estimators, max_features = 1, random_state=3655, n_jobs=-1)
clf.fit(data_np[:,None],y)
indicator, n_nodes_ptr = clf.decision_path(x_grid[:,None])
avg_depth = np.sum(indicator.toarray(), axis=1)/float(n_estimators)
mean_avg_depth = avg_depth/sum(avg_depth)
# 手元でスケール合わせてるの本当は良くない
plt.figure(figsize=(14,7))
plt.hist(data_np, alpha=0.3, bins=20, weights=weights)
plt.plot(x_grid, np.exp(score_bw)*0.7, label="band width=1")
plt.plot(x_grid, mean_avg_depth*6, label="ExtraTrees")
plt.legend()
plt.show()
大まかな二峰性を捉えているものの、先程同様、ギザギザは残ったまんま、二つの峰の高さが揃っていたり、でなんか惜しい感じですね。
PythonKDEパッケージとの実行速度比較
最後に実行速度の比較です。
データは前述ブログに合わせる形で下記のように生成しています。
data_np = 50 * np.random.rand() * np.random.normal(0, 10, n)
x_grid = np.linspace(min(data_np), max(data_np), num=50)
環境は下記です。
・Ubuntu 16.04.2
・Intel(R) Core(TM) i7-6850K CPU @ 3.60GHz
・MemTotal:32856060 kB
・python 3.5.2
やってみましたが、遅い。sklearnKDEと比較して速いとのことだったstatsmodelsKDEも合わせて比べてやろうと思いましたが、足元にも及ばなかった。。。完全ランダム森で全サンプルの最終ノードまで落としていくような木を作るのがやっぱりしんどそう。
| pacakge | n=100 | n=1000 | n=10000 | n=100000 |
|---|---|---|---|---|
| sklearn KDE | 0.00045 | 0.00292 | 0.02989 | 0.44991 |
| statsmodels | 0.00057 | 0.00074 | 0.00325 | 0.02125 |
| sklearn ET | 0.47824 | 0.67802 | None | None |
まとめ
普段教師あり学習に使っている木系アルゴリズムを教師無し的に使ってデータが生まれてくる確率密度推定に活用するネタでした。アイデアとしては見慣れないもので面白いかなと思いましたが、使い勝手はイマイチでした。多次元データでの密度推定などへの対応が必要になるなどがあれば、引き出しとして持っているのは有りかもですが、基本的には慣れ親しんだ推定方法でも大丈夫なのではないでしょうか。