数値変換

この記事の狙い・目的

機械学習を取り入れたAIシステムの構築は、
①データセット作成（前処理）→ ②モデルの構築 → ③モデルの適用
というプロセスで行っていきます。
その際「データセット作成（前処理）」の段階では、正しくモデル構築できるよう、事前にデータを整備しておくことが求めらます。
このブログでは、その際「特徴量エンジニアリング」として用いられることの多い「数値変換」手法について解説していきます。

プログラムの実行環境

Python3
MacBook pro（端末）
PyCharm（IDE）
Jupyter Notebook（Chrome）
Google スライド（Chrome）

データ概要

今回は、一つのデータセットではパターンが足りなかった為、二つのデータセットを使用します。

# データ①取得
churn_modelling = pd.read_csv("./Churn_Modelling.csv")

# データ①確認
churn_modelling.shape
churn_modelling.head()

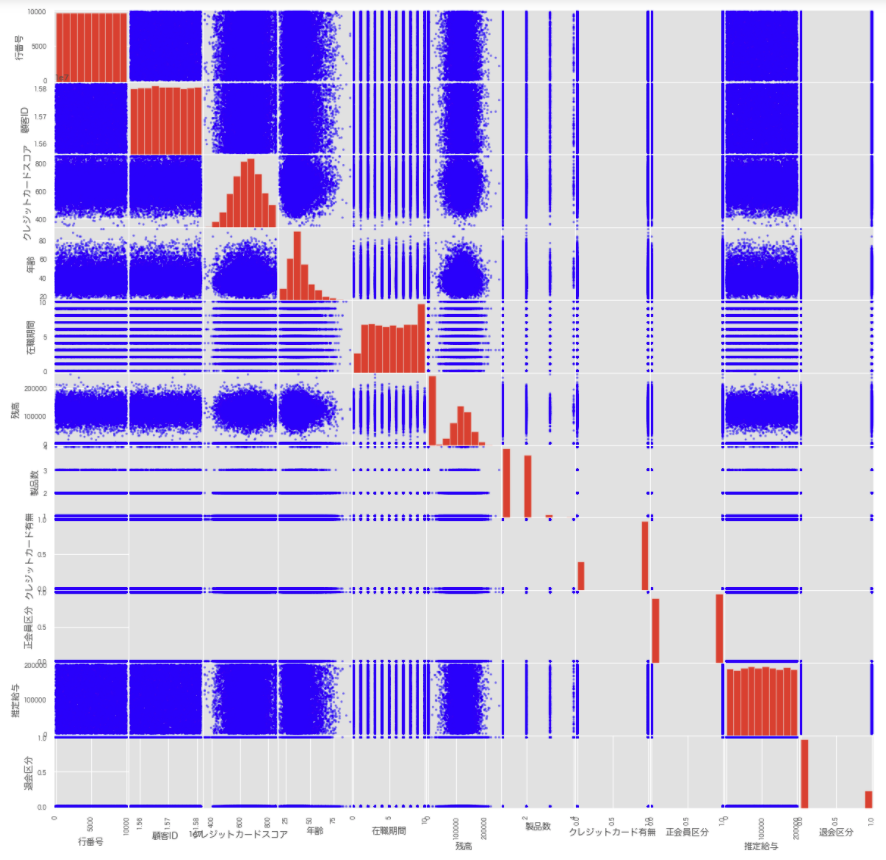
# 散布図行列
pd.plotting.scatter_matrix(churn_modelling, c='blue', figsize=(20, 20))
plt.show();

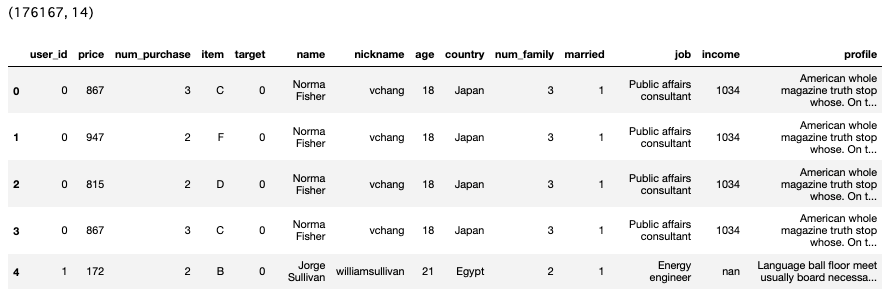
# データ②取得
user_table = pd.read_csv("./user_table.csv")
tran_AtoI = pd.read_csv("./historical_transactions_AtoI.csv")
tran_X = pd.read_csv("./historical_transactions_X.csv")

# 結合（UNION）
train_AtoX=tran_AtoI.append(tran_X, ignore_index=True)

# 目的変数の二値化
train_all = train_AtoX.copy()
train_all['target'] = 0
train_all = train_all.where(train_all['item'] != 'X', 1) # item='X'：正例

# 結合（Left join）
train = pd.merge(train_all, user_table, on='user_id', how='left')

# 目的変数（件数）
train_all['target'].value_counts()

# 散布図行列
pd.plotting.scatter_matrix(train, c='blue', figsize=(20, 20))
plt.show();

数値（量的）データの尺度

間隔尺度

目盛りが等間隔になっているもの：気温

比例尺度

原点があり、間隔や比例に意味があるもの：身長・速度

特徴量生成のパターン（数値変換）

単一変数

二値化、離散化（ビニング）、分位化、べき乗、スケール変換、対数変換、Box-Cox変換、ロジット変換、Yeo-Johnson変換
数学関数による変換（log関数、exp関数、sin関数、cos関数）

複数変数

四則演算（交互作用項・非線形特徴量）、主成分分析、特異値分解、クラスター分析
※時系列データは別記事にて紹介

近似する確率分布の推定

標本データから母集団（全体）の確率分布を推定し、近似する確率分布に応じた適切な手法を選択する必要があります。
今回は概略のみですが、手持ちのデータの母集団がなんらかの分布に従うと仮定し、その母数に対して、統計的推測を行う方法を「パラメトリック法」といいます。具体例としは、最尤推定、ベイズ推定などがあげられます。

数値変数の問題

1.スケールが異なる特徴量
各特徴量間のスケールが大きく異なる場合、機械学習のアルゴリズムは同じスケールのデータを扱うことを前提としており、システムはその数値の大小をそのまま学習してしまい、予期せぬ解釈をしてしまう可能性があります。その為、スケール変換を行い、事前にスケールを調整する必要があります。

2.歪んだ分布
線形回帰モデルでは、出力から得られる値の誤差が正規分布に従うことを仮定しているため、例えば、部分最小二乗法を用いることで説明変数の相関を無相関化するなどの対応が必要になる場合があります。

3.変数間で、線形では表現できないような複雑な関係を持つデータ
データ自体の説明力が強まることがある反面、過学習（オーバーフィッティング）を引き起こす可能性があります。

4.外れ値
k近傍法やサポートベクターマシンは、特徴空間上の外れ値の影響を受けやすい性質があります。アルゴリズムの性質上、データポイント間の距離を捉えており、外れ値が含まれる場合、近傍点の探索や、または境界分離の際の解釈が外れ値に引っ張られる可能性があります。その為、不要な外れ値（異常値）は事前に除去する必要があります。
ただし、実際の値ではなく順位化されたデータを利用する木ベースのモデルでは外れ値の影響を軽減可能です。

5.冗長な情報
重複や不要なデータ（ノイズ）が多く含まれている場合、過学習の危険性が生まれる為、データの簡略化、置換、圧縮等の処理が必要となります。

このような様々な問題に対応する為、数値を適切な形に変換する方法が数多くあります。そのいくつかを今回解説していきます。

変換方法（No.1〜9）

1.二値化

境目（閾値）を設け、"0"と"1"に分ける手法です。
今回は2値分類問題として解くことを想定して、目的変数を生成する過程を紹介します。

# 目的変数の二値化
train_all = train_AtoX.copy()
train_all['target'] = 0
train_all = train_all.where(train_all['item'] != 'X', 1) # item='X'：正例

# データ確認
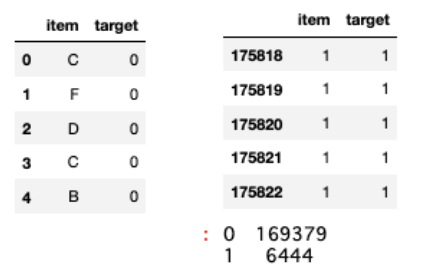
train_all[['item', 'target']].head()
train_all[['item', 'target']].tail()

# 目的変数の確認（件数）
train_all['target'].value_counts()

2.離散化（ビニング）

ある連続した値を不連続な値に分割する手法です。
今回は、年齢を5つの階級に割り当て（分割し）、階級ごとの目的変数の割合や件数を確認していきます。

# 年齢（連続値）を5分割、離散値変換
age = df.copy()
age['年齢層'] = pd.cut(age['年齢'], 5)

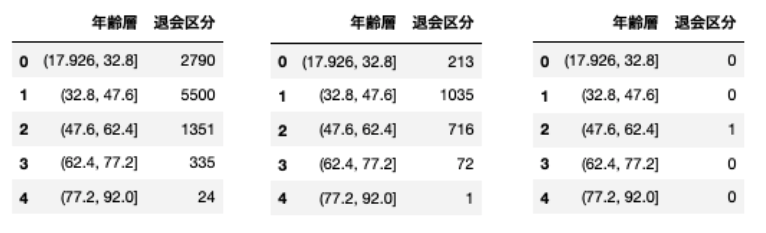
# 年齢層と退会区分で集計
age[['年齢層', '退会区分']].groupby(['年齢層'], as_index=False).count().sort_values(by='年齢層', ascending=True) # 全レコード数
age[['年齢層', '退会区分']].groupby(['年齢層'], as_index=False).sum().sort_values(by='年齢層', ascending=True) # 正例数
age[['年齢層', '退会区分']].groupby(['年齢層'], as_index=False).mean().sort_values(by='年齢層', ascending=True) # 平均（正例が50%以上を1とする）

3.分位化（分位数による離散化）

階級ごとの件数に大きな差がある場合、データの分布に応じて階級を決めるのが分位化（分位数による離散化）という手法です。
今回は、年齢を10分位数で求めた上で離散化していきます。

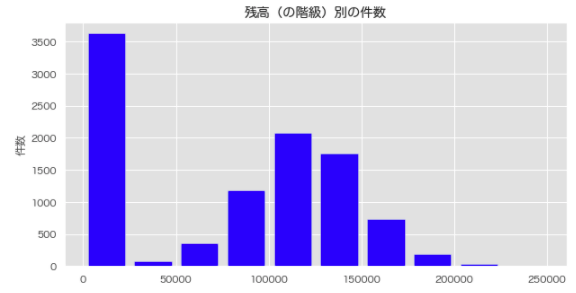
# 十分位数をヒストグラムで可視化する
plt.figure(figsize=[10,5])
plt.hist(df['残高'], rwidth=0.8, color='blue', bins=10) # 10個の階級に分割
plt.title('残高（の階級）別の件数')
plt.ylabel('件数')
plt.show();

4.べき乗

累乗は指数が自然数（生の整数）ですが、べき乗は指数が実数全体となる計算です。

10**2
10**-2
10**(1/2)
10**0.5
10*0

5.スケール変換

スケール変換とは、特徴量がおおよそ同じスケール(寸法、尺度)になるように変換する手法です。
スケール変換にはいくつかの手法がありますが、今回は「StandardScaler」「Normalizer」「MinMaxScaler」について解説していきます。

①StandardScaler（標準化・分散スケーリング）

特徴量の平均が0、分散が1、になるようにスケール変換するアルゴリズム。

from sklearn.preprocessing import StandardScaler

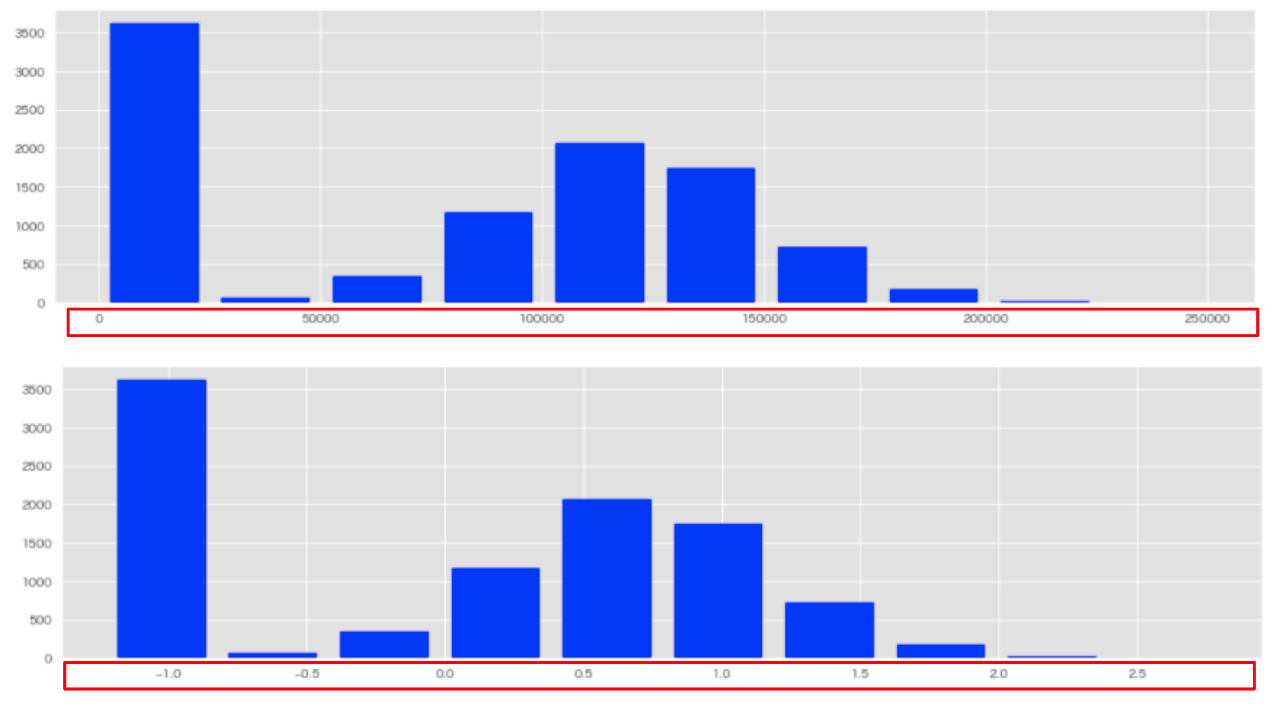
plt.figure(figsize=[15,3])
# 変換前
plt.hist(df['残高'], rwidth=0.8, color='blue', bins=10)

# 標準化
std = df.copy()
scaler = StandardScaler()
std['残高'] = scaler.fit_transform(std[['残高']])
std['残高'].head().astype(str)

# 変換後
plt.hist(std['残高'], rwidth=0.8, color='blue', bins=10)

②Normalizer（正規化）

特徴量（ベクトル）のノルムが1になるようにスケール変換するアルゴリズム。
デフォルトでは、L2正規化が適用されています。

from sklearn.preprocessing import Normalizer

nrm = df.copy()
X = nrm[['残高']].values
X = X.reshape(1, -1)

# 正規化（L2ノルム）
transformer2 = Normalizer(norm='l2').fit(X)
nl2 = transformer2.transform(X)

# データフレームに変換
nrm_df2 = pd.DataFrame(data=nl2.reshape(-1, 1), columns=["正規化_残高"])
nrm_df2.astype(str).head()

plt.hist(nrm_df2, rwidth=0.8, color='blue', bins=10);

nrm = df.copy()
X = nrm[['残高']].values
X = X.reshape(1, -1)

# 正規化（L1ノルム）
transformer1 = Normalizer(norm='l1').fit(X)
nl1 = transformer1.transform(X)

# データフレームに変換
nrm_df1 = pd.DataFrame(data=nl1.reshape(-1, 1), columns=["正規化_残高"])
nrm_df1.astype(str).head()

plt.hist(nrm_df1, rwidth=0.8, color='blue', bins=10);

③MinMaxScaler（最大絶対値による正規化）

特徴量の値が一定の範囲（0から1、または-1から1）に収まるようにスケール変換するアルゴリズム。

from sklearn.preprocessing import MinMaxScaler

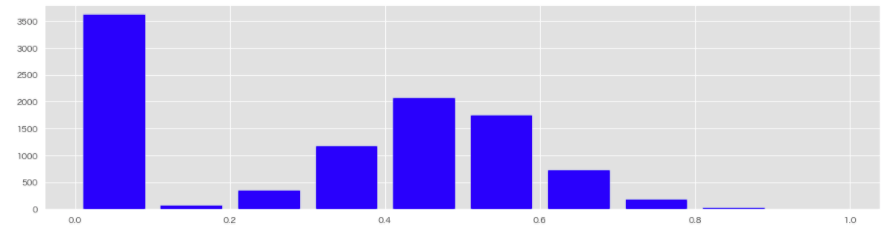
mm_df = df.copy()
mm = MinMaxScaler(feature_range=(0, 1), copy=False)
mm_df['残高_mm'] = mm.fit_transform(mm_df[['残高']])
mm_df['残高_mm'].astype(str).head()

plt.hist(mm_df['残高_mm'], rwidth=0.8, color='blue', bins=10);

標準化や正規化におけるモデル別の注意点

決定木ベースのモデル（決定木、ランダムフォレスト）では、特徴量を入力とする複数のステップ関数（閾値を超えた場合に1, そうでなければ0に変換する）の組み合わせによって構成されるため、変数のスケールの影響を受けません。
ロジスティック回帰や部分最小二乗法、リッジ回帰や距離を利用するk-means、主成分分析など、多くのモデルは入力のスケールに敏感で、変数間のスケールを揃える必要があります。
また、リッジ回帰、主成分分析では入力に用いる変数間のスケールが標準化されていることが前提です。それは特徴量空間におけるデータ間の距離を利用するためです。

6.対数変換

特徴量のスケールが大きい時はその範囲を縮小し、小さい時は拡大する手法です。
裾の重い（縦長の）分布に対して、上方の長い裾を圧縮し、下方の短い裾を拡大し、より偏りの少ない山形の分布にすることができるようになります。
分散が大きなデータでは平均値が大きいほど等分散となりやすい傾向があります。

tgt_name = 'income'
log_tgt_name ='log_income'
# 対数変換
train_log = train.copy()
train_log[log_tgt_name] = np.log10(train[tgt_name] + 1)

# 変換前
fig, (ax1, ax2) = plt.subplots(2, 1)
train_log[tgt_name].hist(ax=ax1, bins=100)
ax1.tick_params(labelsize=14)

# 変換後
train_log[log_tgt_name].hist(ax=ax2, bins=100)
ax1.tick_params(labelsize=14)

7.Box-Cox変換

データを指定の分布（※正規分布）に近づける手法。0や負値を扱えない点に要注意です。

from scipy import stats

def box_cox(df, tgt, lmbda):
    df = train.copy()

    tgt = tgt
    bxcx = df.copy()

    tgt_log = stats.boxcox(bxcx[tgt], lmbda=lmbda) # 分布の指定
    # lmbda=0 : 対数変換（縮小化）
    # lmbda=0.5 : 平方根変換（縮小化）
    # lmbda=1以上 : 拡大化

    tgt_bc, tgt_params = stats.boxcox(bxcx[tgt]) # 0, 負数を扱えない
    tgt_params
    
    bxcx['tgt_log'] = tgt_log
    bxcx['tgt_bc'] = tgt_bc

    fig, (ax1, ax2, ax3) = plt.subplots(3,1)

    bxcx[tgt].hist(ax=ax1, bins=100, figsize=[20, 15])
    ax1.set_yscale('log')
    ax1.tick_params(labelsize=14)
    ax1.set_title(f'{tgt}のヒストグラム')

    bxcx['tgt_log'].hist(ax=ax2, bins=100, figsize=[20, 15])
    ax2.set_yscale('log')
    ax2.tick_params(labelsize=14)
    ax2.set_title(f'{tgt}のヒストグラム（対数変換後）')

    bxcx['tgt_bc'].hist(ax=ax3, bins=100, figsize=[20, 15]);
    ax3.set_yscale('log')
    ax3.tick_params(labelsize=14)
    ax3.set_title(f'{tgt}のヒストグラム（最適なbox-cox変換後）');

tgt = 'income'
lmbda = 0 # lmbda=0 : 対数変換（縮小化）
box_cox(df, tgt, lmbda)

8.ウィンザー化

一定の範囲外のデータを除外する手法です。外れ値処理などに活用できます。

# パーセンタイルの取得
tgt = 'income'
df = user_table.copy()
Q1 = df[tgt].quantile(.25) # 25%
Q3 = df[tgt].quantile(.75) # 第三位分位

# 閾値の算出
IQR = Q3 - Q1
IQR

# 四分位範囲（IQR）の1.5倍以上以下を外れ値とする
threshold = Q3 + 1.5 * IQR
threshold

# 外れ値の検出
df_outlier = df[df[tgt].apply(lambda x:x > threshold)]
df_outlier[[tgt]].head()

9.ロジット変換

ロジット変換とは、一言で言えば、なにかしらの比例xを、オッズの自然対数に変換することです。
オッズとは、なにか（x）が起こる確率（p）を、なにか（x）が怒らない確率（1-p）で割った、割合のことです。
これを自然対数で変換すると、（確率値などの）0〜1の間の数を、正負両方向に無限大の値に変換できることになります。
この計算はロジスティック回帰で用いられており、図で値の変遷を可視化するとシグモイド関数の図となります。

import math
math.log(0.6 / (1 - 0.6))

# 結果：0.4054651081081642

まとめ

今回は数値変換の様々な手法を紹介しました。今回は割愛してしまいましたが、他にも多くの手法があることを執筆の過程で学ぶことができました。
またそれぞれの手法では、前提として仮定する確率分布があります。（今回は割愛してしまいましたが）母集団の確率分布を推定する方法についても、別記事で紹介したいと思います。

最後に

他の記事はこちらでまとめています。是非ご参照ください。

参考文献

統計Web 変数の尺度
統計Web パーセンタイル
統計Web ロジット変換
統計Web ロジスティック回帰分析(5)─ロジスティック変換の逆変換
sklearn.preprocessing.Normalizer

解析結果

実装結果：GitHub/churn_modeling.ipynb
実装結果：github/purchase_forecast_feature.ipynb
データセット：Churn Modelling classification data set - kaggle

参考資料