クラスタリング

この記事の狙い・目的

機械学習を取り入れたAIシステムの構築は、
①データセット作成（前処理）→ ②モデルの構築 → ③モデルの適用
というプロセスで行っていきます。
その際「データセット作成（前処理）」の段階では、正しくモデル構築できるよう、事前にデータを整備しておくことが求めらます。
このブログでは、その際「特徴量エンジニアリング」として用いられることの多い「クラスタリング」手法と、またその手法を用いて行う「特徴量生成」について解説していきます。

プログラムの実行環境

Python3
MacBook pro（端末）
PyCharm（IDE）
Jupyter Notebook（Chrome）
Google スライド（Chrome）

クラスタリングとは

クラスタリングとは、あるデータをなんらかの規則に従ってグループ分けすることです。そして、グルーピングされたそれぞれのデータ群をクラスタと呼びます。
ビジネスシーンでもよく用いられる「クラスタリング」ですが、実際にどのようなシーンで活用されるのかをまずは見ていきましょう。

①ECサイトの顧客分析
マーケティング活動の効率化を目的として、市場における自社顧客をグループ化（セグメンテーション）やその可視化を行う際にクラスター分析として用いられることがあります。

②機械学習を取り入れたAIシステムの構築
特にデータセットの作成工程では、構築モデルの精度向上を目的として、特徴量の生成に用いられることがあります。

今回は機械学習における活用方法について、もう少し詳しく解説していきます。
クラスタリングは「教師なし学習」に分類されます。つまり正解ラベルがない状態でデータをグループ分けしていきます。
そして、クラスタリングには大きく分けて「階層的クラスター分析」と「非階層的クラスター分析」の２つの手法があります。
ビジネスシーンでよく用いられるのは非階層的クラスター分析の方です。
それぞれについて、もう少し詳しく解説していきましょう。

1.階層クラスタリング

階層クラスタリングとは、最も似ているサンプル同士を１つずつ順番にグルーピングしていく手法です。
そして、クラスター同士の類似度を測る方法には主に以下の３つの方法があります。

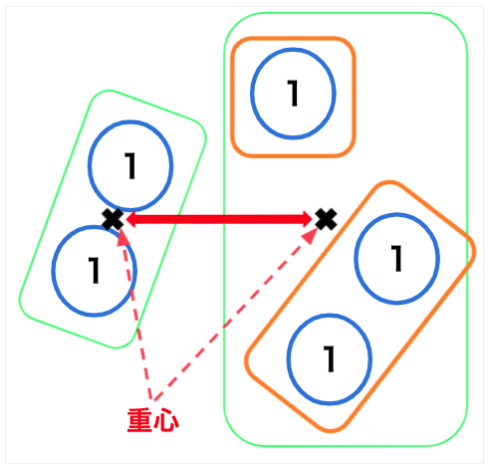
重心法

２つクラスターの互いの重心間の距離をクラスター間の距離として類似度を測る方法。

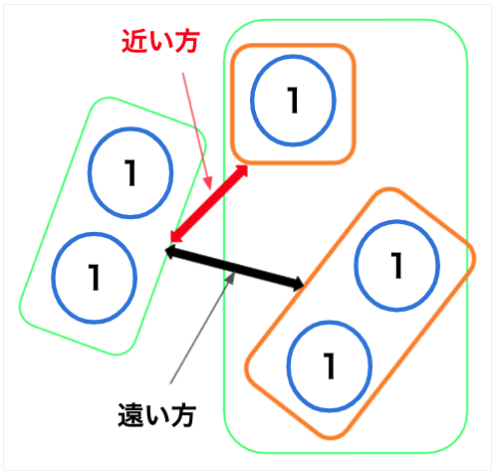
最短（最長）距離法

２つのクラスタ―に含まれるデータの中で、最もお互いに近い（遠い）データ同士の距離をクラスター間の距離として類似度を測る方法。

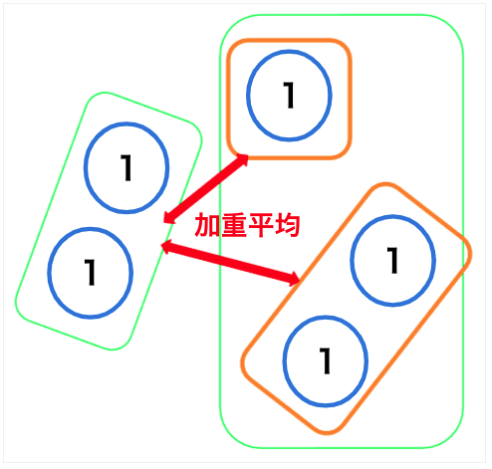
群平均法

各クラスター同士で、全ての組み合わせのサンプル間距離の平均をクラスター間距離として類似度を測る方法。

# デンドログラム
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt
%matplotlib inline

def plot_dendrograme(df):
   li=linkage(df.corr())
   r=dendrogram(li, labels=df.columns)
   plt.figure(figsize=[20,5])
   plt.show()

# ワインデータ
wine_data = wine_df.copy()
dframe = pd.DataFrame()
dframe['項目名']  = wine_df.columns
dframe

number_list = list(range(0,13))
wine_data.columns = number_list
plot_dendrograme(wine_data)

# 顧客（取引）データ
plot_dendrograme(wholesale_drop)

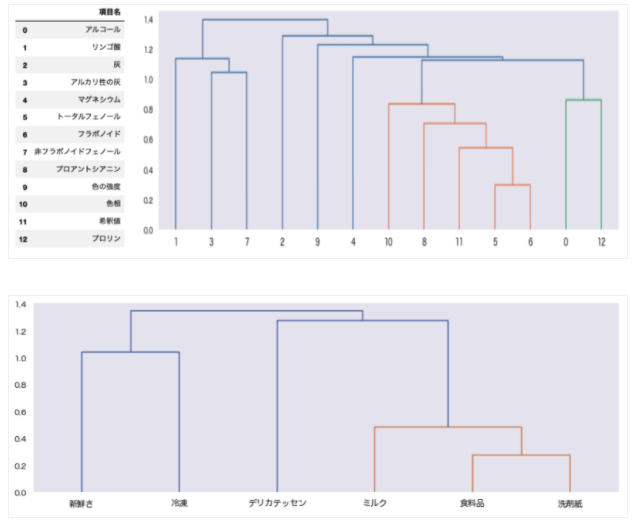
ワインデータについては、「5:トータルフェノール」も「6:フラボノイド」の一種であることから、感覚的にも分類が合っていそうです。また「7:非フラボノイドフェノール」が「5:トータルフェノール」が離れた位置にあることからも、分類は合っていそうです。

顧客（取引）データについて、「食料品」と「ミルク」の方が近しい分類になると思っていましたが、「食料品」と「洗剤紙」の方が近しい結果となっています。一緒に購入されることが多いためでしょうか。この点は別の分析方法を用いて新たな知見を得ていく必要がありそうです。
※今回は割愛させていただきます。

2.非階層クラスタリング

非階層クラスタリングとは、あらかじめ決めたクラスタ数に、データを分割する手法です。

k-means法

代表的な手法として「K-means法」というものがあります。
K-means法とは、あらかじめいくつのクラスターに分類するかを指定し、クラスター内では分散が小さく、クラスター間では分散が大きくなるようにデータを分割する（クラスターに振り分ける）手法です。

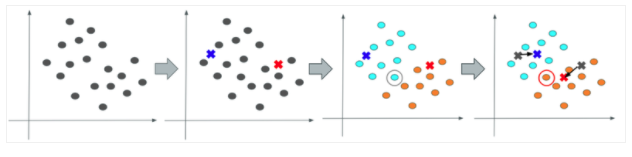
ここではそのアルゴリズムをステップ４に分けて解説していきます。

ステップ１
初期値となる重心点を、指定数だけ、ランダムで決定・配置します。

ステップ２
各データから最も近い重心点を算出し、クラスタを構成します。
この時、重心点までの距離の計算には「ユークリッド距離」「マンハッタン距離」「コサイン距離」などを用いることがあります。

ステップ３
２で構成したクラスタごとに重心を再度算出します。

ステップ４
３で求めた重心が２で求めた重心と異なる場合は、再度２〜３を実施します。これを２と３の変化がなくなるまで繰り返し実行します。

K-means法の長所・短所

K-means法はとてもシンプルなアルゴリズムではありますが、長所と短所がある為、活用に際しては考慮しておきましょう

1.K-means法の長所

K-means法は、階層クラスタリングと比べ、べてのデータ間の距離を計算する必要がなくなるため、計算コストが低く、大規模なデータに対しても実行速度が早いという長所があります。

2.K-means法の短所

最初の重心の指定はランダムに行うため、同じ母集団でも計算する度に分類結果が少し変わってしまうことがあります。
また、外れ値があるとデータの拡散により、結果的にクラスタ同士が離れてしまい、正しく分類できない場合があります。
複雑なデータや、特定の方向に分散したデータをうまく分類できないケースがあります。
これらに対する対応方法についてしていきます。

クラスタリングの注意点

それでは実際にクラスタリング（クラスター分析）を実施する、クラスタリングの注意点についても触れておきましょう。
様々なシーンで用いられることが多いクラスタリング（クラスター分析）ですが、実際に分析を始める前に注意しないといけない点があります。
それは事前に分析の目的や仮説を明確にしておくことです。
目的や仮説がないままに分析を実施しても、データを分類することに終始し、それ以上の考察を得られない可能性があります。
そのデータセットのセグメント分けはどのようなものが考えられそうか、セグメント分けの結果は何に役立てていくのか、といった点を考えて置く必要があります。

また実装の際、（データによっては）特徴量を「平均0、標準偏差1に標準化」する必要があります。
これはスケールの異なるデータに対して算出した（ユークリッド）距離同士を均等に解釈できない為です。

今回のデータ分析の目的

今回は分類結果の比較をするため、２つのデータセットを扱います。その為、それぞれの分析目的を以下に記載します。

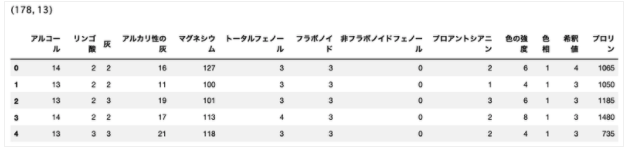
データセット（１）：ワインの品質データ
ワインの品質（レベル感）を把握し、改善が必要なグループを検出すること。

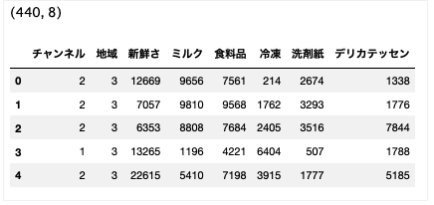
データセット（２）：卸売業者の顧客（取引）データ
取引情報から顧客の属性を把握し、アプローチするターゲット層を見つけること。

クラスタリング

それでは実際に実装と結果を見ていきましょう。
まずはデータ確認からです。今回は２つのデータセットのクラスタリング結果を比較して確認していきます。

# データ取得①（ワインデータ）
from sklearn import datasets
import pandas as pd

wine = datasets.load_wine()
wine_df = pd.DataFrame(wine.data, columns=wine.feature_names) # データフレームに変形

# リネーム
name_list = ['アルコール','リンゴ酸','灰','アルカリ性の灰','マグネシウム','トータルフェノール','フラボノイド','非フラボノイドフェノール','プロアントシアニン','色の強度','色相','希釈値','プロリン']
wine_df.columns = name_list
wine_df.shape
wine_df.head()

# データ取得②（卸売りの顧客データ）
wholesale_customers = pd.read_csv("./wholesale_customers_data.csv")

# データ概要
wholesale_customers.head()
wholesale_customers.shape

# クラスタリング（k-means）
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
import seaborn as sns

def clustering(df, num):
   sc = StandardScaler()
   sc.fit_transform(df)
   data_norm = sc.transform(df)

   cls = KMeans(n_clusters = num)
   result = cls.fit(data_norm)
   pred = cls.fit_predict(data_norm)

   plt.figure(figsize=[10, 5])
   sns.set(rc={'axes.facecolor':'cornflowerblue', 'figure.facecolor':'cornflowerblue'})
   sns.scatterplot(x=data_norm[:,0], y=data_norm[:,1], c=result.labels_)
   plt.scatter(result.cluster_centers_[:,0], result.cluster_centers_[:,1], s=250, marker='*', c='blue')
   plt.grid('darkgray')
   plt.show()

# ワインデータ
clustering(wine_data, 3)

# 顧客（取引）データは、取引商品情報以外の項目を除外
wholesale_drop = wholesale_customers.copy()
wholesale_drop = wholesale_drop.drop(columns=['チャンネル', '地域'])
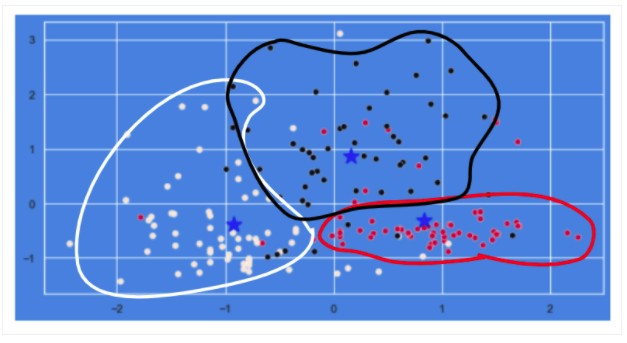
clustering(wholesale_drop, 3)

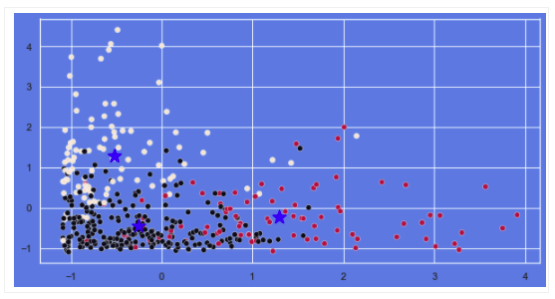
ワインデータについては、おおよそ３つのクラスターに振り分けられているように見られます。
顧客（取引）データについては、外れ値の除去も行なっていない為、データの拡散が見られ、またデータの重なりも多く、クラスター数が３で適当かは判断が難しいところです。

エルボー法

顧客（取引）データについては、クラスター数について判断が難しいところがありました。そのような時に有効な手法として「エルボー法」というものがあります。
エルボー法とは、最適なクラスター数の探索する手法の一つです。
グラフのX軸に「クラスター数」、Y軸に「SSE（クラスタ内誤差平方和）」を取ります。
**SSE（クラスター内誤差平方和）**とは、クラスタリングの性能を評価する指標の一つで、各データ（データポイント）と属しているクラスタの中心点（セントロイド）との距離（ユークリッド距離）の総和を表しています。
実装と結果を見ていきましょう。

# クラスター数の探索
def elbow(df):
   wcss = []

   for i in range(1, 10):
       kmeans = KMeans(n_clusters = i, init = 'k-means++', max_iter = 300, n_init = 30, random_state = 0)
       kmeans.fit(df.iloc[:, :])
       wcss.append(kmeans.inertia_)

   plt.figure(figsize=[10,4])
   plt.plot(range(1, 10), wcss)
   plt.title('エルボー法')
   plt.xlabel('クラスター数')
   plt.ylabel('クラスター内平方和（WCSS）')
   plt.grid()
   plt.show()

# ワインデータ
elbow(wine_df)

# 顧客（取引）データ
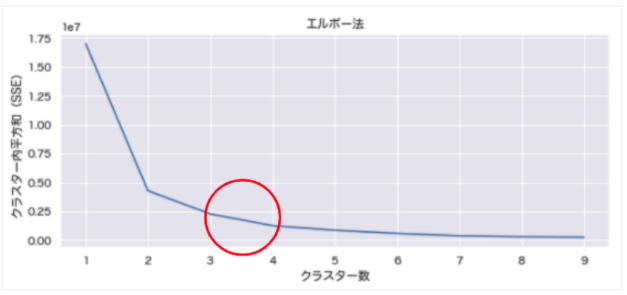
elbow(wholesale_drop)

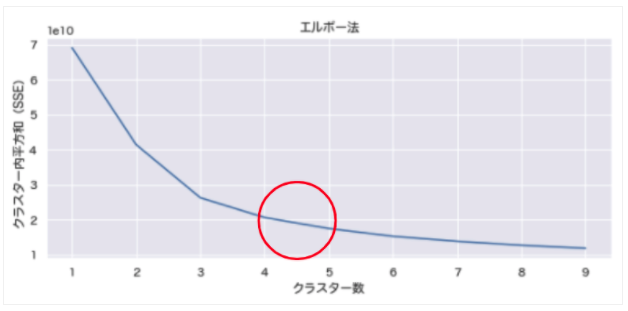
ワインデータのクラスターは想定の通り「クラスター数=3」で問題なさそうです。
顧客（取引）データは「クラスター数=4〜5」が妥当という結果になりました。この後の章で再度、解析していきます。

クラスタリング＋主成分分析

ここではクラスタリングと主成分分析（次元圧縮）を併用した結果で解説していきます。

## クラスタリング（k-means）＋主成分分析
from sklearn.decomposition import PCA

def cross(df, num):
   df_cls = df.copy()
   sc = StandardScaler()
   clustering_sc = sc.fit_transform(df_cls)

   kmeans = KMeans(n_clusters=num, random_state=42) # n_clusters：クラスター数
   clusters = kmeans.fit(clustering_sc)
   df_cls['cluster'] = clusters.labels_

   x = clustering_sc
   pca = PCA(n_components=num) # n_components：削減結果の次元数
   pca.fit(x)
   x_pca = pca.transform(x)
   pca_df = pd.DataFrame(x_pca)
   pca_df['cluster'] = df_cls['cluster']

   for i in df_cls['cluster'].unique():
       tmp = pca_df.loc[pca_df['cluster'] == i]
       plt.scatter(tmp[0], tmp[1])
   plt.grid()
   plt.show()

# ワインデータ
cross(wine_df, 3)

# 顧客（取引）データ
# クラスター数を４に設定して、再度クラスタリングを実施
cross(wholesale_customers, 4)

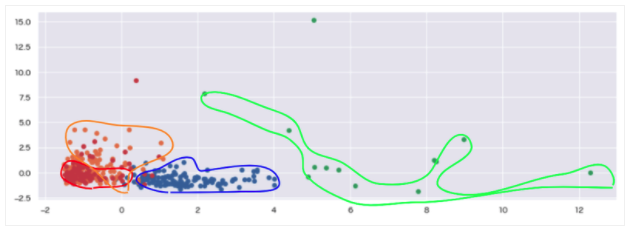
周辺の外れ値が４つめのクラスターとして分類され、全部で４つのクラスターにおおまかに分類できました。しかし、データポイントの重なりも多く、綺麗な形で分類はできていないことがわかります。

# 顧客（取引）データ
# 外れ値を除去したデータで再度クラスタリングを実施
cross(wholesale_drop, 4)

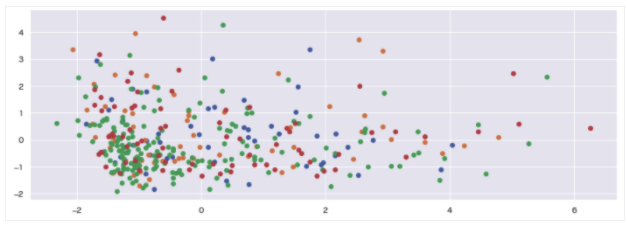
データの拡散は解消されたましたが、クラスターごとのデータポイントの重なりが非常に増え、各クラスターの構成要素に共通点が多いことがわかります。綺麗な形では分類できない為、別のグラフで可視化して解析することにします。

積み上げ棒グラフ

積み上げ棒グラフとは、カテゴリー別に各データ群の構成要素を積み上げて可視化するグラフです。実際に見ていきましょう。

def clustering_pred(df):
   sc = StandardScaler()
   sc.fit_transform(df)
   data_norm = sc.transform(df)

   cls = KMeans(n_clusters = 4)
   pred = cls.fit_predict(data_norm)

   df['クラスターID']=pred
   
   return df

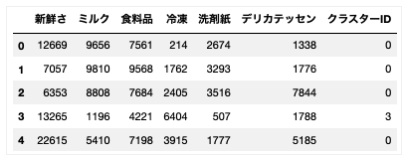
result = clustering_pred(wholesale_drop)
result.head()

# 積み上げ棒グラフ
cluster = pd.DataFrame()
for i in range(4):
   cluster['クラスター' + str(i+1)] = wholesale_drop[wholesale_drop['クラスターID'] == i].mean()
cluster = cluster.drop('クラスターID')

plt.figure(figsize=[20,5])
my_plot = cluster.T.plot(kind='bar', stacked=True, title="各クラスタの平均")
my_plot.set_xticklabels(my_plot.xaxis.get_majorticklabels(), rotation=0)
plt.grid()

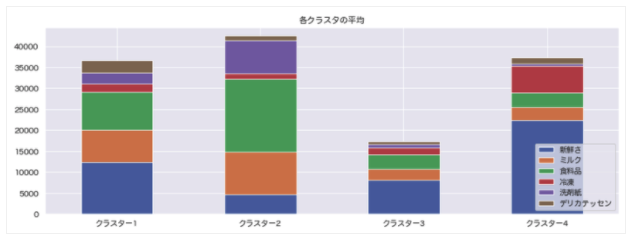
積み上げ棒グラフでの可視化により、各セグメント（顧客）の構成要素の把握ができるようになりました。
セグメント別に見ると、クラスタごとに、構成要素（各変数）の割合が異なっていることがわかる。
クラスタ1：「新鮮さ・食料品・ミルク」が多い
クラスタ2：「新鮮さ・食料品・ミルク・洗剤紙」が多い、比重は少なめ
クラスタ3：「新鮮さ」が多い、比重は少なめ　　
クラスタ4：「食料品・冷凍」が多い

K-Means++法

K-Means++法とは、K-Means法の拡張手法の一つで、K-Means法の短所である初期値に分類結果が依存する問題の解決を試みた手法です。
具体的には、初期の中心点をランダムで設定するのではなく、各データポイント間の距離に基づいて確率的に決定するところが、K-Means法と異なっています。

# クラスタリング（KMeans++）＋主成分分析
def cross(df, num):
   sc = StandardScaler()

   df_cls = df.copy()
   clustering_sc = sc.fit_transform(df_cls)

   kmeans = KMeans(n_clusters=num, # n_clusters：クラスター数
                   init='k-means++', # 中心の設定、中心店点（セントロイド）の初期値をk-means++法で選択
                   n_init=10, # 異なる初期値を用いた実行回数
                   max_iter=1000, # 最大イテレーション回数  default: '300'
                   tol=1e-04, # 許容する誤差
                   random_state=42
                  )
   clusters = kmeans.fit(clustering_sc)
   df_cls['cluster'] = clusters.labels_

   x = clustering_sc
   pca = PCA(n_components=num) # n_components：削減結果の次元数
   pca.fit(x)
   x_pca = pca.transform(x)
   pca_df = pd.DataFrame(x_pca)
   pca_df['cluster'] = df_cls['cluster']

   for i in df_cls['cluster'].unique():
       tmp = pca_df.loc[pca_df['cluster'] == i]
       plt.scatter(tmp[0], tmp[1])
   plt.grid()
   plt.show()

# ワインデータ
cross(wine_df, 3)

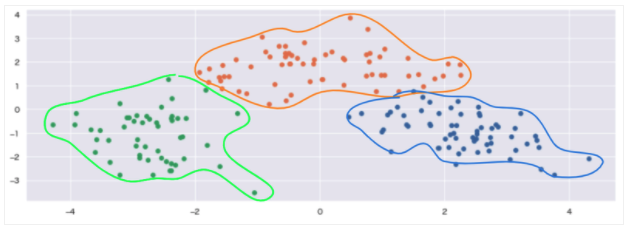
データ数が少なくシンプルな構造の為か「k-means ⇆ k-means」を比較しても、あまり大きな変化は見られませんでした。

# 顧客（取引）データ
cross(wholesale_drop, 4)

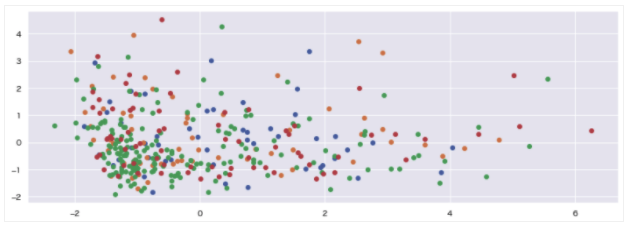
こちらも「k-means ⇆ k-means」の結果を比較しても、あまり大きな変化は見られませんでした。
各セグメントの構成要素を分析する目的からも、やはり積み上げ棒グラフでの可視化が効果的と思われる。

特徴量生成

最後に、クラスタリングを用いて新たな特徴量を生成する方法を紹介します。
各データポイントと各クラスタの重心との距離を捉える方法になります。
構築モデルの予測精度に対する影響は別記事で考察することとさせていただきます。

# 重心からの距離
num_cluster=3 # cluster数
clusters = KMeans(n_clusters=num_cluster, random_state = 42)
clusters.fit(wine_cut)
centers = clusters.cluster_centers_

columns = wine_cut.columns
clust_features = pd.DataFrame(index = wine_cut.index)
for i in range(len(centers)):
   clust_features['クラスタ' + str(i + 1) + 'との距離'] = (wine_cut[columns] - centers[i]).applymap(abs).apply(sum, axis = 1)
clust_features

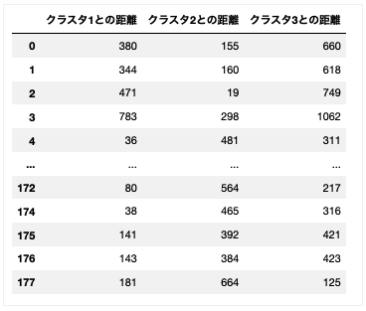
これで各レコードと、各重心との距離を表現することができました。

まとめ

今回は、いろいろなシーンで活用されるクラスタリングについて解説してきました。そもそも論として、なんのためにクラスタリングを行うのかという点が分析においてとても重要な点であることがわかりました。
今回は紹介しませんでしたが、K-Means法にはその拡張手法として「kMedoids、xmeans、Mini Batch K-Means」など（K-Means++法意外にも）様々な手法が存在します。Mini Batch K-Meansは、大規模データ向けのk-means法です。
また、クラスタリングのアルゴリズムには、K-Means法意外にも「DBSCAN、Mean Shift、Gaussian Mixture Model」などの様々なアルゴリズムが存在します。こちらも別のデータセットを取り扱った際に紹介していきたいと思います。

最後に

他の記事はこちらでまとめています。是非ご参照ください。

参考文献

クラスタリング - 神嶌 敏弘
ハラノビスの距離入門 - 救仁郷 誠
国立情報学研究所：ｋ-means法の様々な初期値設定によるクラスタリング結果の実験的比較
日本食品分析センター：ポリフェノール（特にフラボノイド）について
東京大学 - ベクトル量子化

解析結果

実装結果：GitHub/clustering.ipynb
データセット：sklearn.datasets.load_wine
データセット：Wholesale customers Data Set - UCI

参考資料