不均衡データ

記事の狙い・目的

機械学習を取り入れたAIシステムの構築は、
①データセット作成（前処理）→ ②モデルの構築 → ③モデルの適用
というプロセスで行っていきます。
その際「データセット作成（前処理）」の段階では、正しくモデル構築できるよう、事前にデータを整備しておくことが求めらます。
このブログでは、その際に問題なることが多い、「不均衡データ」とその対処方法について解説していきます。

プログラム等の実行環境

Python3
MacBook pro（端末）
PyCharm（IDE）
Jupyter Notebook（Chrome）
Google スライド（Chrome）

不均衡データとは

不均衡データとは「データ構造に偏りがあり、負例または正例データの片方が極端に少ない（インバランスな）データ群」のことを言います。

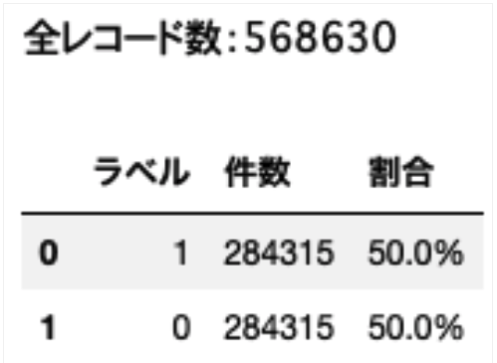
※負例データ(ラベル=0)は、正例データ(ラベル=1)の577倍にあります。

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

# データ取得
creditcard = pd.read_csv("./creditcard.csv", sep=',')

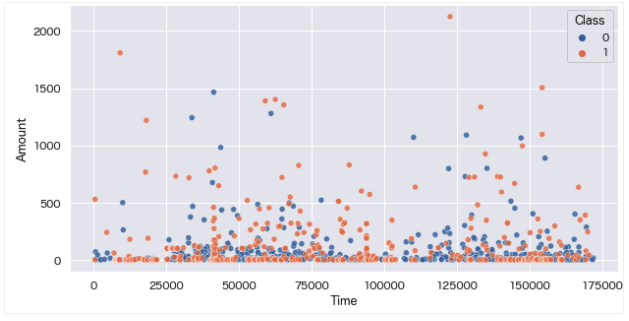
data = creditcard[creditcard['Amount']<5000][['Time', 'Amount', 'Class']]
plt.figure(figsize=[10,5])
plt.grid()
sns.scatterplot(data = data, x ='Time', y = 'Amount', hue = 'Class', alpha=0.8)

不均衡データの問題点

データ構造に偏りがあると何が問題なのでしょうか。
それは、例えば正例データが非常に多く、負例データが極端に少ないデータを用いて予測モデルを構築した場合、予測結果は正例となることが多く、本来負例のデータを精度良く予測することが困難となります。
またその結果、（予測結果のほとんどが正例となることで）一見精度（正解率(Accuracy)）は高く評価されますが、適合率(Precision)・再現率(Recall)は低い結果となってしまいます。

もう少し詳しく解説していきます。
上記のデータセットを用いて、負例データが284315件、正例データが492件のデータセットがあるとします。
そして評価結果を混同行列で表した場合、下記の結果となったとします。

import numpy as np
from sklearn.svm import SVC # サポートベクトルマシン
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score

def plot_confusion_matrix(predict, y_test):
   pred =  np.where(predict > 0.5, 1, 0)
   cm = confusion_matrix(y_test, pred)
   matrix = pd.DataFrame(cm)
   matrix.columns = [['予測_負例(0)', '予測_正例(1)']]
   matrix.index = [['実際_負例(0)', '実際_正例(1)']]
   return matrix

# サポートベクトルマシン
svc = SVC()
svc.fit(X_train, y_train)
y_pred = svc.predict(X_test)

# 混同行列
matrix = plot_confusion_matrix(y_pred, y_test)
matrix

# 評価
print('Accuracy = ', accuracy_score(y_true=y_test, y_pred=y_pred).round(decimals=3))
print('Precision = ', precision_score(y_true=y_test, y_pred=y_pred, zero_division=0).round(decimals=3))
print('Recall = ', recall_score(y_true=y_test, y_pred=y_pred).round(decimals=3))
print('F1 score = ', f1_score(y_true=y_test, y_pred=y_pred).round(decimals=3))

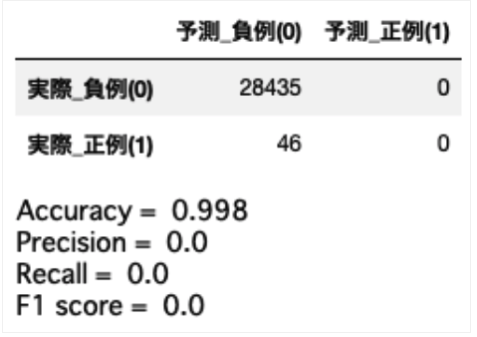
これは極端な例ですが、Accuracyが約99%となっており一見非常に精度良く予測できているように見えますが、Recallが0%となっており、1件も正例データを正しく予測できていないことがわかります。

また不均衡データのもう一つの問題点として、"余計な"計算コストがある。
例えば多数派のデータが豊富にあった場合でも、そのほとんどが似通ったデータであり、識別境界付近にないデータの場合、それらをいくら学習しても汎化性能の向上は期待できない為、結果的に無駄な計算をしてしまっていることがあります。
その為、処理速度を改善したい場合は、適切な方法を用いてデータセットを作成する必要があります。

%%time
# サポートベクトルマシン
svc = SVC()
svc.fit(X_train, y_train)
y_pred = svc.predict(X_test)

処理に21.3秒掛かっており、若干長めです。

不均衡データを扱う際の注意点

上記の通り、不均衡データをそのまま分析・学習してしまうと問題があることがわかりました。
その為、不均衡データを扱う際、分析・学習目的に即した対応が必要となります。

例えば学習の結果、正解率(Accuracy)が高い予測モデルを構築するこが目的だった場合を仮定します。
その場合は、目的に即した結果となる為、不均衡データに対する特別は対応は不要となるかもしれません。
しかし、反対に漏れなく負例を予測したい場合は、目的と合致しない予測モデルができあがってしまうことになります。
その為、不均衡データを扱う際には、その主目的、および想定の評価結果に即した対応が必要となります。
詳しくは「不均衡データに対するアプローチ」の章で解説していきます。

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

x = creditcard.drop('Class',axis=1)
y = creditcard['Class']

# データ分割
X_train,X_test,y_train,y_test = train_test_split(x,y,test_size=0.1, random_state=42)

# ロジスティック回帰
lr = LogisticRegression(max_iter=1000)
lr.fit(X_train, y_train)
y_pred = lr.predict(X_test)

# 混同行列
matrix = plot_confusion_matrix(y_pred, y_test)
matrix

# 評価
print('Accuracy = ', accuracy_score(y_true=y_test, y_pred=y_pred).round(decimals=3))
print('Precision = ', precision_score(y_true=y_test, y_pred=y_pred).round(decimals=3))
print('Recall = ', recall_score(y_true=y_test, y_pred=y_pred).round(decimals=3))
print('F1 score = ', f1_score(y_true=y_test, y_pred=y_pred).round(decimals=3))

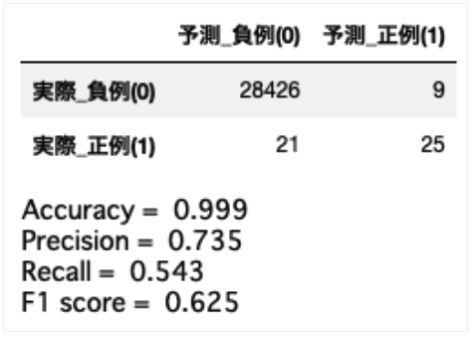
上記の通り、正解率(Accuracy)は99%であり、負例データのほとんどは正しく予測することができています。
しかし適合率(Precision)を見てみると54%となっており（全正例：46件の内）54%=25件しか正しく予測できていないことがわかります。正例データを漏れなく予測したい場合は非常に精度が悪く、改善が必要であることがわかります。

不均衡データの発生原因

不均衡データに対するアプローチについて解説する前に、不均衡データの発生原因についても見ていきましょう。
発生原因の一つとして、正例(または負例)データの発生確率が極端に低いケースがあげられます。
非常に稀な病気の発症有無と観測した場合、データの大半は未発症者(負例)となり、発症者(正例)はごく僅かとなります。
その他、例えば店舗での取扱数の少ない商品分類の購入予測を行う際にも、対象カテゴリーの母数がそもそも少ないことから、その購買履歴は不均衡データとなってしまうケースがあります。
最終的な評価指標の期待値は、分析・学習目的に由来する為、どのような背景で不均衡データとなっているのか事前に考察しておく必要があります。

不均衡データに対するアプローチ

それでは不均衡データに対するアプローチについて解説していきます。
ここでは代表的なものとして5つの手法を取り上げていきます。

1.アンダーサンプリング

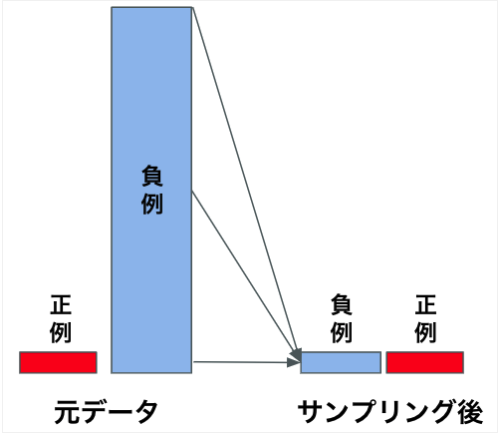
アンダーサンプリングとは、多数派のデータを少数派のデータ数に合わせて削除する手法です。

# アンダーサンプリング
from imblearn.under_sampling import RandomUnderSampler

target = 'Class'
rs = RandomUnderSampler(random_state=42)
under_sampling ,_ = rs.fit_resample(creditcard, creditcard[target])

print('*'*20)
print('＜元のデータ＞')
print('0の件数：%d'%len(creditcard.query(f'{target}==0')))
print('1の件数：%d'%len(creditcard.query(f'{target}==1')))
print('*'*20)
print('＜アンダーサンプリング後のデータ＞')
print('0の件数：%d'%len(under_sampling.query(f'{target}==0')))
print('1の件数：%d'%len(under_sampling.query(f'{target}==1')));

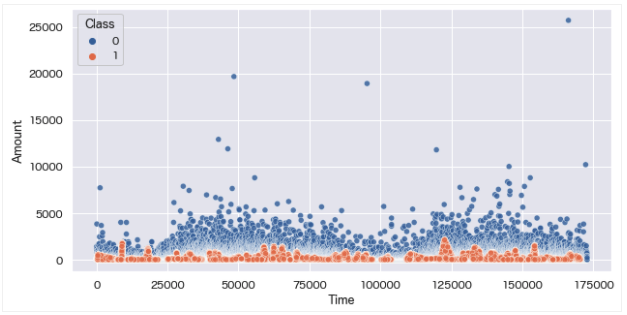
data = under_sampling[['Time', 'Amount', 'Class']]
plt.grid()
sns.scatterplot(data = data, x ='Time', y = 'Amount', hue = 'Class', alpha=0.8)

※正例データ(Class=1)のデータの増加を視認でき、Amount > 3000以上のデータが削除されていることがわかります。

上記の通りアンダーサンプリングはとてもシンプルな手法ですが、注意点として、多数派のデータを削除している為、重要なデータまでもが欠損し、元の多数派のデータに対しバイアスが生じる原因となってしまう点があげられます。
その為、確率予測をする場合、アンダーサンプリングを行ったデータで構築したモデルが出力する予測確率に生じるバイアスを除去し、補正する必要が生じます。
アンダーサンプリングによるバイアスの補正方法は「Calibrating Probability with Undersampling for Unbalanced Classification」で紹介されていますが、詳細について今回は割愛させていただきます。

2.アンダーバギング

アンダーサンプリングには、学習した分類(予測)器の出力の分散が大きくなる（ことがある）という問題があります。
アンダーサンプリング後のデータ量が十分でない場合、的確な予測ができず予測結果にちらばりが生じてしまうことがあります。
その為、アンダーバギングという手法が有効なケースがあります。
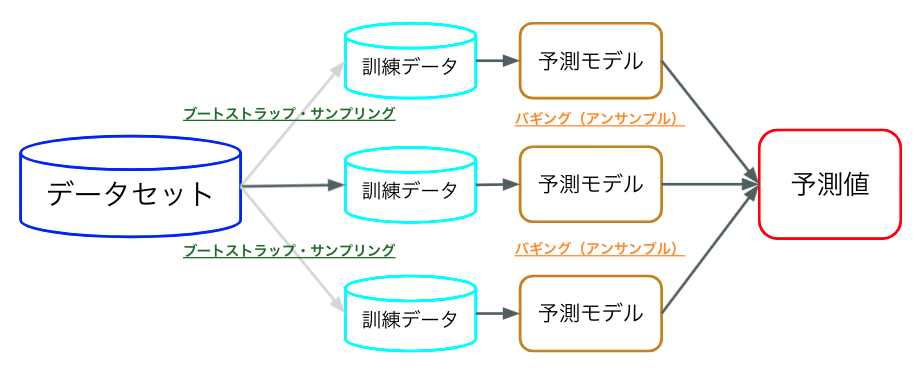
アンダーバギングとは、アンダーサンプリングを実施してk通りの部分集合を作成し、各部分集合ごとに分類器を学習し、バギングでアンサンブルする手法です。
ここで言うバギングとは、ブートストラップサンプリング手法を用いて生成したデータを、複数のモデルでそれぞれ学習する方法です。
ブートストラップサンプリングとは、置換を伴うランダムサンプリングのことです。これによりデータの平均化（偏りをなくす）を行います。

import lightgbm as lgb # LightGBM
from tqdm import tqdm # プログレスバー

def lgbm_train(X_train, X_valid, y_train, y_valid):
   model = lgb.LGBMClassifier(
       objective='binary',
       metric='auc',
       boosting_type='gbdt',
       num_leaves=30,
       learning_rate=0.01,
       feature_fraction=0.9,
       subsample=0.8,
       max_depth=12,
       min_data_in_leaf=12)
   model.fit(X_train, y_train)
   return model

# バギング
def bagging(seed):
   # アンダーサンプリング
   sampler = RandomUnderSampler(random_state=seed, replacement=True)
   X_resampled, y_resampled = sampler.fit_resample(X_train, y_train)
   model_bagging = lgbm_train(X_train2, X_valid, y_train2, y_valid)
   return model_bagging

# データ分割
X = creditcard.drop(columns='Class', axis=1)
y = creditcard['Class']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=42)
X_train2, X_valid, y_train2, y_valid = train_test_split(X_train, y_train, test_size=0.1, random_state=42)

# 学習
models = []
for i in tqdm(range(10)):
   models.append(bagging(i))

# 予測
y_preds = []
for m in tqdm(models):
   y_preds.append(m.predict(X_test))

# 評価
y_preds_bagging = sum(y_preds)/len(y_preds)
auc = roc_auc_score(y_test, y_preds_bagging)
print(f'AUC： {round(auc, 2)}')

# 混同行列
matrix = plot_confusion_matrix(y_preds_bagging, y_test)
matrix

# 評価
print('Accuracy = ', accuracy_score(y_true=y_test, y_pred=y_preds_bagging).round(decimals=3))
print('Precision = ', precision_score(y_true=y_test, y_pred=y_preds_bagging, zero_division=0).round(decimals=3))
print('Recall = ', recall_score(y_true=y_test, y_pred=y_preds_bagging).round(decimals=3))
print('F1 score = ', f1_score(y_true=y_test, y_pred=y_preds_bagging).round(decimals=3))

結果、アンダーサンプリング＋バギングにより、正例と予測した32件は正しく予測できていることがわかります。
ただし、実際は正例のものを負例と予測してしまっているものが12件ある為、まだまだ改善の余地はありそうです。

3.オーバーサンプリング

オーバーサンプリングとは、アンダーサンプリングとは反対に、少数派のデータを多数派のデータ数に合わせて増やしていく手法です。

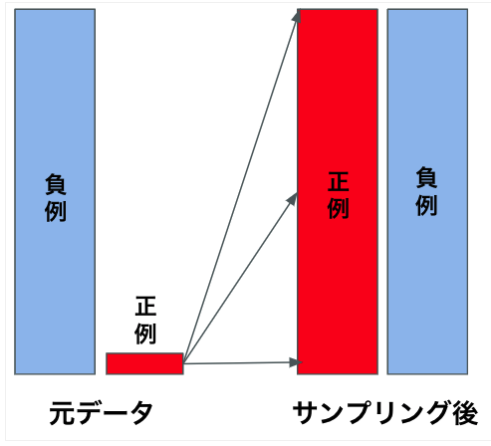
ただし、少数派のデータをただ単純に複製するだけでは、データセットに新しいバリエーションを持たせることはできません。
つまり、オーバーサンプリングの注意点として、無秩序に少数派のデータを量増ししたところで、同じようなデータが増えることで過学習に陥り、汎化性能の低い予測モデルを構築してしまうことになってしまいます。
その対象方法として代表的なものに「SMOTE (Synthetic Minority Oversampling TEchnique)」という手法がしばしば使用されます。
SMOTEとは、ランダムサンプリングのデータと、k近傍法のアルゴリズムで求められたデータにより、合成データを作成する方法です。

ここではSMOTEについて、もう少し詳しく解説していきます。
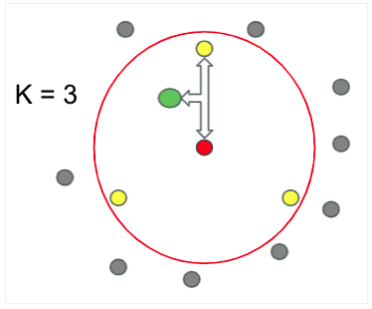
SMOTEは、まず少数派のデータからランダムでデータを選択し、そのデータからランダムで選択された近傍点を用いて、両者の合成データを作成します。
下記はK=3の時の例です。赤丸を中心点として、近傍点(黄色丸)を３つ選択します。そしてその中からランダムで１つの近傍点を選択し中心点と近傍点の間に新たなサンプル(緑丸)を生成します。

# SMOTE
from imblearn.over_sampling import SMOTE

sm = SMOTE(random_state=42)
X = creditcard.drop(columns='Class', axis=1)
y = creditcard['Class']
X_sample, Y_sample = sm.fit_resample(X, y)

over_sampling = pd.DataFrame()
over_sampling = X_sample
over_sampling['Class'] = Y_sample

value_counts = over_sampling['Class'].value_counts()

df = pd.DataFrame()
df['ラベル'] = value_counts.index
df['件数'] = value_counts.values
ratio=[]
ratio.append((value_counts.values[0] / len(over_sampling['Class']) * 100).round(decimals=2).astype('str'))
ratio.append((value_counts.values[1] / len(over_sampling['Class']) * 100).round(decimals=2).astype('str'))
df['割合'] = [f'{ratio[0]}%', f'{ratio[1]}%']
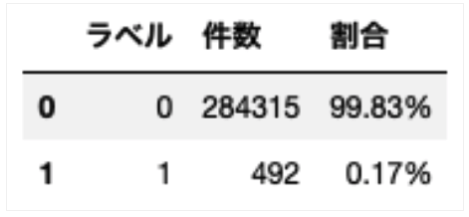
print(f"全レコード数：{len(over_sampling['Class'])}")
df

data = over_sampling[['Time', 'Amount', 'Class']]
plt.grid()
sns.scatterplot(data = data, x ='Time', y = 'Amount', hue = 'Class', alpha=0.8)

data = over_sampling[over_sampling['Amount']<5000][['Time', 'Amount', 'Class']]
plt.grid()
sns.scatterplot(data = data, x ='Time', y = 'Amount', hue = 'Class', alpha=0.8)

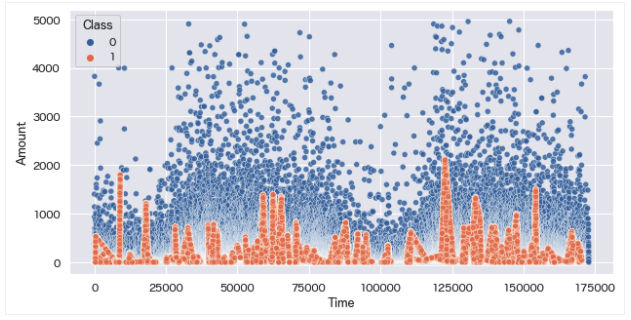
もともと正例データ(Class=1)は、Amount=2000以下に分布していたことから、オーバーサンプリング後もAmount=2000以下の正例データが量産されていることがわかります。

4.重み付け

少数派のサンプルに重み付けを行い（重要視して）、少数派のカテゴリをより的確に分類できるようにする手法です。
重み付けとは、目的関数の誤差に対し（少数派データのラベルごとに）ペナルティを与え、少数派のデータの学習を重視して学習させることを言います。
というのも、例えば決定木系のモデルでは、損失関数を元に分類を行いますが、そもそも正例または負例のサンプル少ない場合は、損失に影響を及ぼしにくい為、重み付けを行う必要があります。

重み付けのメリットとしては、メモリを節約して不均衡データに対応できるようになることがあります。
なぜならオーバーサンプリングのように、データ量の増加は発生しない為です。
また重み付け注意点として、重み付け学習データにのみに対して行い、検証データ、テストデータに対しては重み付けを行なってはいけない点があります。
なぜなら、実際のデータの比率に対しての精度を見て評価を行わないといけないからです。

def add_weight(weight):
   # データ分割
   X = creditcard.drop('Class',axis=1)
   y = creditcard['Class']
   X_train,X_test,y_train,y_test = train_test_split(X, y, test_size=0.1, random_state=42)

   # ロジスティック回帰
   lr_w = LogisticRegression(max_iter=1000, class_weight=weight)

   lr_w.fit(X_train, y_train)
   y_pred = lr_w.predict(X_test)

   # 混同行列
   matrix = plot_confusion_matrix(y_pred, y_test)

   # 評価
   print('Accuracy = ', accuracy_score(y_true=y_test, y_pred=y_pred).round(decimals=3))
   print('Precision = ', precision_score(y_true=y_test, y_pred=y_pred).round(decimals=3))
   print('Recall = ', recall_score(y_true=y_test, y_pred=y_pred).round(decimals=3))
   print('F1 score = ', f1_score(y_true=y_test, y_pred=y_pred).round(decimals=3))

   return matrix

weights = 'balanced' # 重みの自動調整
matrix = add_weight(weights)
matrix

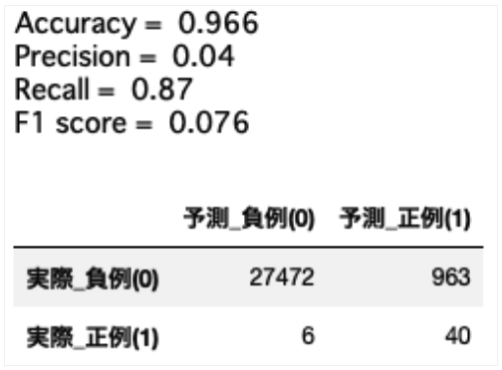
「比例の逆数 / クラス数」の重み付けにより、正例をより多く予測するモデルを構築することができました。
結果、再現率Recallが上昇し、より多くの正例データを予測することができています。

念の為「weights = 'balanced'」の計算式についても解説しておきます。

n_samples = len(creditcard['Class']) # 全サンプル数
n_classes = 2 # 全クラス数
np.bincount(y) # 正例・負例件数
# 計算式
weight = n_samples_0 / (n_classes * np.bincount(y))
weight

「class_weight='balanced'」では、入力データのクラス頻度に反比例する重みを算出しています。計算式としては「比例の逆数 / クラス数」を求めているようです。

5.異常検知問題として扱う

これまでアンダーオーバーサンプリング、重み付けについて解説してきました。
ただし、あまりにもデータに偏りがあり正例データが不足しており、尚且つ少数派のデータがクラスターを作れていない場合、分類問題として扱うのは困難なケースがあります。
その時は、分類問題ではなく、異常検知問題としてのアプローチが有効なケースがあります。
正常データ群からの距離や密度の違いに着目し、事前に定めた閾値を超えたデータを異常値として判定する手法です。

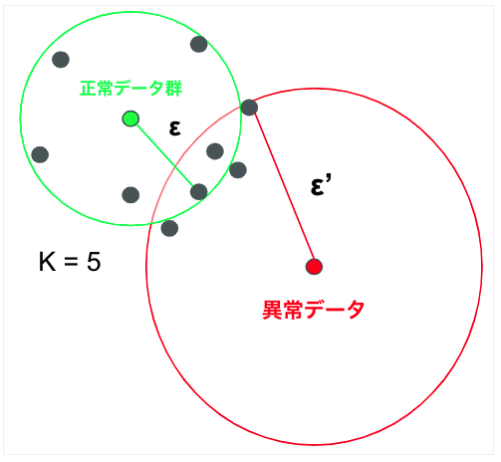
今回はあまり深い入りしませんが、異常検知手法については簡略に紹介しておきます。
・Local Outlier Factor (LOF)
　k近傍法ベースのアルゴリズム
・One-class SVM
　サポートベクトルマシンの改良版
・Isolation Forest (iForest)
　ランダムフォレストと似たアルゴリズム
「Local Outlier Factor (LOF)」については「外れ値検出について」でもう少し詳しく解説しています。​

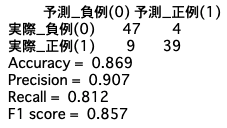
不均衡データの評価指標

冒頭で少し触れましたが（改めて）不均衡データを用いた際の予測モデルの評価指標について解説していきます。
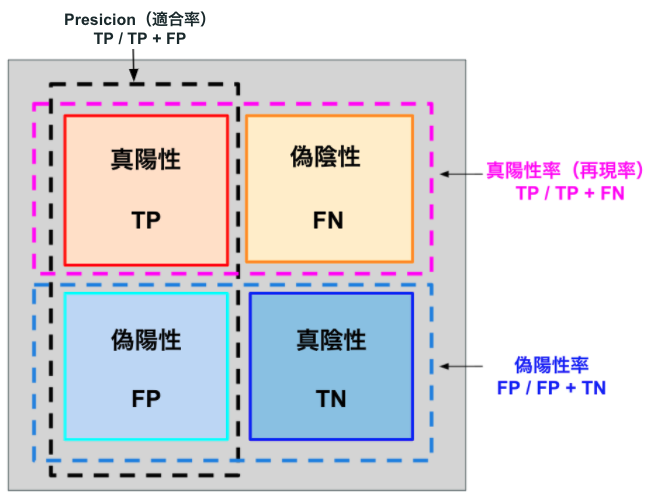
代表的な評価指標は以下の４つがあります。
・正解率:Accuracy
・適合率:Precision
・再現率:Recall
・F値（F-measure）
適合率:Precisionは、どれだけ間違いなく正例データを予測できているか、
再現率:Recallは、どれだけ漏れなく正例データを予測できているか、
F値（F-measure）は、適合率と再現率の調和平均です。

from sklearn import metrics
from sklearn.metrics import roc_auc_score # ROC曲線

def modeling(data):
   X = data.drop('Class',axis=1)
   y = data['Class']

   # データ分割
   X_train,X_test,y_train,y_test = train_test_split(X, y, test_size=0.1, random_state=42)

   # ロジスティック回帰
   lr = LogisticRegression(max_iter=1000)
   lr.fit(X_train, y_train)
   y_pred = lr.predict(X_test)

   # 混同行列
   matrix = show_confusion_matrix(y_pred, y_test)
   print(matrix)

   # 評価
   print('Accuracy = ', accuracy_score(y_true=y_test, y_pred=y_pred).round(decimals=3))
   print('Precision = ', precision_score(y_true=y_test, y_pred=y_pred).round(decimals=3))
   print('Recall = ', recall_score(y_true=y_test, y_pred=y_pred).round(decimals=3))
   print('F1 score = ', f1_score(y_true=y_test, y_pred=y_pred).round(decimals=3))

   return lr, y_pred, X_train, X_test, y_train, y_test

# ROC曲線
def plot_roc_curve(pred, y_test):
   pred =  np.where(pred > 0.5, 1, 0.5)
   fpr, tpr, thresholds = metrics.roc_curve(pred, y_test)
   plt.figure(figsize=[15, 5])
   plt.plot(fpr, tpr, label=f'roc_curve')
   plt.xlabel('FPR')
   plt.ylabel('TPR')
   plt.legend()
   plt.grid()
   plt.show()

   auc = metrics.auc(fpr, tpr)
   print('auc: {:.3f}'.format(auc))

# PR（Precision-Recall）曲線
def plot_precision_recall_curve(y_test, y_pred):
   precision, recall, thresholds = metrics.precision_recall_curve(y_test, y_pred)

   auc = metrics.auc(recall, precision)
   print(f'AUC： {round(auc,3)}%')

   plt.figure(figsize=[15, 5])
   plt.plot(recall, precision, label='PR curve (area = %.2f)'%auc)
   plt.legend()
   plt.title('PR curve')
   plt.xlabel('Recall')
   plt.ylabel('Precision')
   plt.grid()
   plt.show();

# アンダーサンプリング
lr, y_pred, X_train, X_test, y_train, y_test = modeling(under_sampling)

# ROC曲線
plot_roc_curve(y_pred, y_test)

# Precision-Recall曲線
plot_precision_recall_curve(y_test, y_pred)

ここでは評価結果の確認方法として「ROC曲線」と「PR曲線」について解説しておきたいと思います。
1番目の画像は、ROC（Receiver Operating Characteristic）曲線です。
X軸に「偽陽性率（=FPF）」、Y軸に「真陽性率（=TPF）（Recallと同義）」を取ることで曲線を描いたグラフです。また、グラフの下の部分の面積をAUC（Area Under the Curve）と呼びます。AUCは0から1までの値をとり、値が1に近いほど判別性能が高いことを示します。つまり、予測精度が高い場合、曲線の下の面積が広がる傾向を見ることができます。
評価スコアを見てみると「Recall:0.81」となっており、「Recall：どれだけ正解も漏れなく予測できたか」を重視する場合は、もう少しROC曲線の曲線の下の面積が広くてもよいかもしれません。
また、ROC曲線は評価軸に「偽陽性率」を用いているため、真陽性（TN）の評価も考慮しています。今回のような不均衡データでは負例件数が非常に多く、正例に対する予測をある程度間違えてもスコアが高く出てしまうことがあります。そこで注目されるのが以下の「PR曲線」です。

2番目の画像が、PR（Precision-Recall）曲線です
このグラフは、X軸に「Recall（再現率）」、Y軸に「Precision（適合率）」をとっています。
ROC曲線と比較すると、多少曲線の下の面積が狭くなっており、Recallの評価をより反映したグラフとなっていることがわかります。したがって、今回のような不均衡データを取り扱い、特にRecallの評価を見たい場合などにはPR曲線を確認した方がよいと言えるでしょう。
参考に評価指標の違いを図示しておきます。

最後に学習曲線を見ると、検証データに対するスコアも90%以上に収束していっている為、過学習ではなさそうです。しかし両者のスコアが近く、学習結果に偏りがある（バイアスが高い）かもしれません。

まとめ

今回初めてアンダーバギングを行ってみましたが、ブートストラップサンプリングを用いてランダムにダウンサンプリングするのではなく、クラスタリングを用いたサンプリングに切り替えるなど、まだまだ改善の余地はありそうだと思いました。
オーバーサンプリングについても、単純に少数派を多数派に合わせて増やすだけでは既存の少数派データと同じような値を増やすだけとなってしまい、特徴空間の識別に有意となる値を増やせていなかったり、少数派データの中でも偏りのあるデータを増やしてしまったりする可能性も考えると、多数派のアンダーサンプリングと、少数派のオーバーサンプリングをセットで行うなどの方法を検討する必要があると思いました。
どのようなシチュエーションで活用しているのかは、「特徴量エンジニアリング」の記事で総括してまとめていきます。

最後に

他の記事はこちらでまとめています。是非ご参照ください。

参考文献

統計Web 検査精度
scikit-learn Machine Learning ：ロジスティック回帰（公式ドキュメント）
scikit-learn Machine Learning ：適合率-再現率（公式ドキュメント）
不均衡データにおけるアンダーサンプリングによる分類精度向上法
Calibrating Probability with Undersampling for Unbalanced Classification

解析結果

実装結果：GitHub/creditcard.ipynb
データセット:Credit Card Fraud Detection - kaggle

参考資料