ガウス過程回帰やSVMで出てくるカーネル法に関する簡単なメモ。
数学的な証明は省きます。
発想
回帰問題と分類問題を考えてみる。
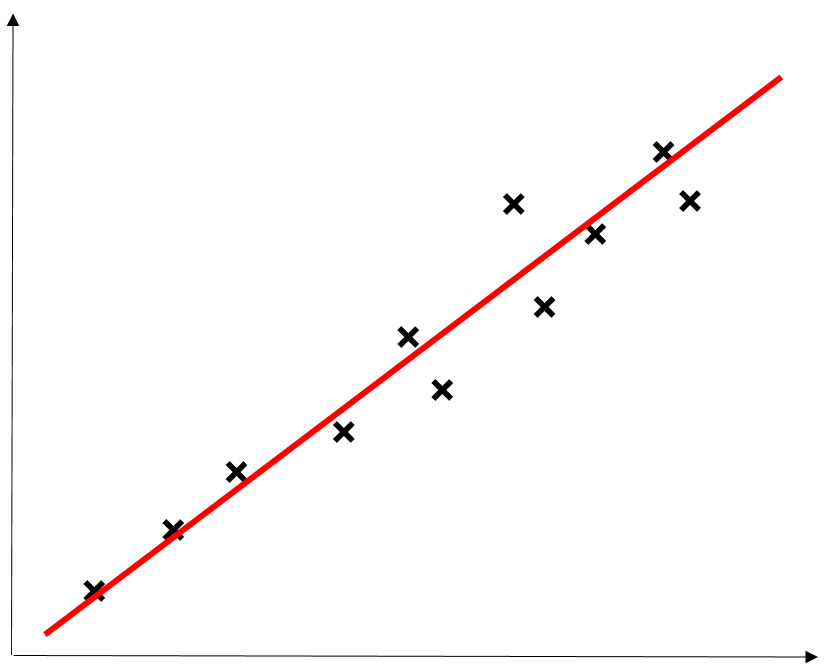
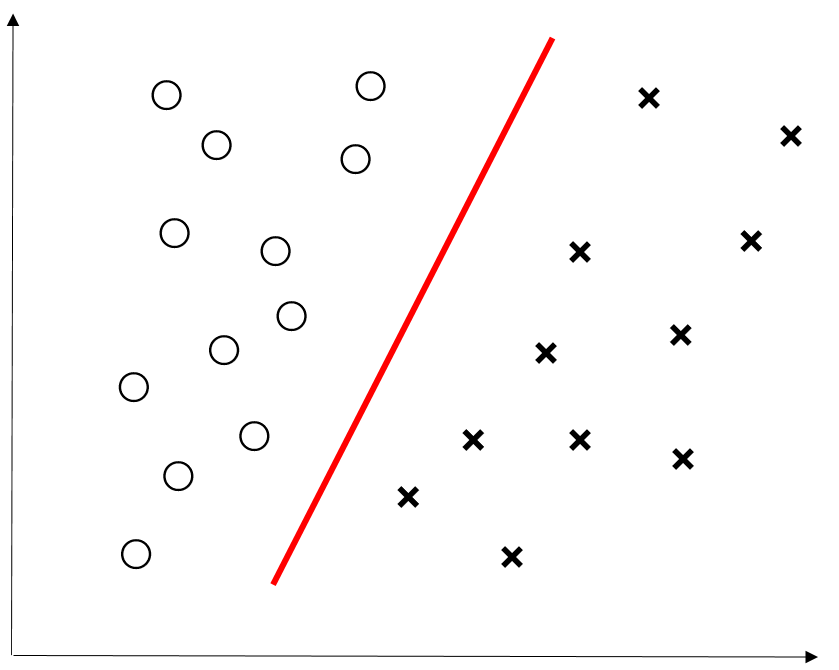
以下の2つの例は1次関数で回帰、分類ができる。
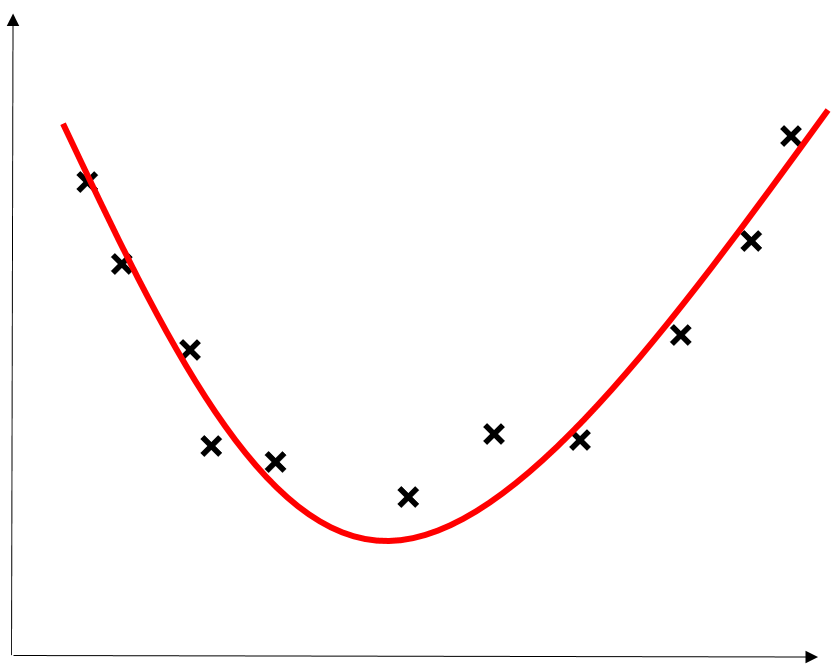
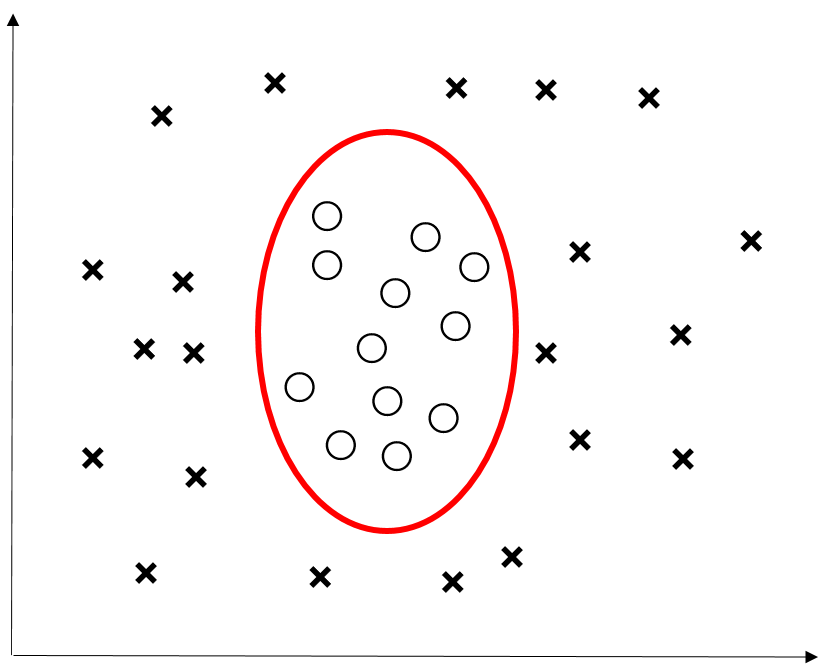
しかし、以下の例では1次関数での回帰、分類ができない。
1次関数での取り扱いは簡単なので、下2つの例でも1次関数での回帰、分類がしたい。
そこで、1次関数での回帰、分類ができるようにデータを別の空間に変換する。
カーネル関数から定まる再生核ヒルベルト空間の構成
流れ
カーネル関数を定義
↓
カーネル関数から構成されるベクトル空間 $\mathcal{V}$ の定義
↓
$\mathcal{V}$ に内積を定める
↓
$\mathcal{V}$ の内積の完備化(再生核ヒルベルト空間の構成)
まずカーネル関数を定義しよう。
$X$を集合とし、$k$を$X$上の2変数関数とする。$k$が以下の2つの条件を満たすとき
$k$は$X$上のカーネル関数という。
条件1(対称性)
任意の$x,y\in X$に対して
k(x,y) = k(y,x)
が成り立つ。
条件2(半正定値性)
任意の$n\in \mathbb{N}, \{x_1,\cdots,x_n\} \subset X ,\{c_1, \cdots ,c_n\}\subset \mathbb{R}$に対して
\sum_{i,j=1}^{n}c_i c_j k(x_i, x_j) \geq 0
が成り立つ。
カーネル関数から内積を構成しよう。まず、カーネル関数$k$に対して、$k_x(y)=k(y,x)$とおき、$k_x$を1変数関数として扱う。$\{k_x\}_{k\in X}$で生成されるベクトル空間を
\mathcal{V} = \Biggl\{ \sum_{j=1}^{n}a_j k_{x_j} \quad | \quad x_j \in X, a_j \in \mathbb{R}, n \in \mathbb{N} \Biggr\}
とおく。
次に、$f=\sum_i a_i k_{x_i}, g=\sum_j b_j k_{y_j} \in \mathcal{V}$に対し、
\langle f,g\rangle_{\mathcal{V}} = \langle \; \sum_{i}a_i k_{x_i}, \sum_{j}b_j k_{y_j} \; \rangle_{\mathcal{V}}=\sum_{i,j}a_i b_j k(y_j, x_i)
と定めると、$\langle \cdot ,\cdot \rangle_{\mathcal{V}}$はwell-definedであり、内積の定義を満たす。この内積に基づいた完備化を考えれば、カーネル関数$k$から構成される再生核ヒルベルト空間$\mathcal H_k$が得られる。
再生核ヒルベルト空間では以下の等式が成り立つ
再生核等式
任意の$x \in X$と任意の$f\in \mathcal H_k$に対し、
f(x) = \langle f, k_x \rangle_{\mathcal{H}_k}
が成り立つ。すなわち、関数$f\in \mathcal H_k$に点$x\in X$を代入する操作が$k_x=k(\cdot,x)$との内積で表される。この$k_x$は再生核とよばれる。
カーネル法による回帰例
回帰問題において、データ$\boldsymbol x_1, \cdots \boldsymbol x_n\in \mathbb R^d$と$y_1, \cdots y_n \in \mathbb R$が与えられたとする。このとき、データ$\boldsymbol x_j$を$k_{\boldsymbol x_j}=k(\cdot,\boldsymbol x_j)$に変換する事を考える。(カーネルトリック)
この変換先の空間こそが、上で構成した再生核ヒルベルト空間である。
ちなみに、この変換する際の写像
\Phi : \boldsymbol{x}_j \mapsto k_{\boldsymbol{x}_j}
は特徴写像とよばれる。一般に、変換先の空間の事を特徴空間とよぶ。
問題設定
$k$を$\mathbb{R}^d$上のカーネル関数とし、$\mathcal H_k$を$k$から構成される再生核ヒルベルト空間とする。このとき、
\{\boldsymbol{x_1}, \cdots ,\boldsymbol{x_n} \} \subset \mathbb{R}^d, \boldsymbol{y}=(y_1,\cdots,y_n)^T \in \mathbb{R}^nに対し、\\ L(f) = \sum_{j=1}^{n}|f(\boldsymbol{x_j})-y_j|^2 (f\in\mathcal{H}_k)\\を最小化するf\in\mathcal{H}_kを求めよ。
解法
$P$を$\mathcal H_k$内で $\{ k_{\boldsymbol x_1},\cdots,k_{\boldsymbol x_n}\}$ により張られる空間への直交射影とする。このとき、ヒルベルト空間内での射影定理から$f$は$f=Pf+(f-Pf)$と直交分解できる。よって、再生核等式より
f(\boldsymbol x_i)=\langle f, k_{\boldsymbol x_i}\rangle_{\mathcal H_k}=\langle Pf+(f-Pf),k_{\boldsymbol x_i}\rangle_{\mathcal H_k}=\langle Pf,k_{\boldsymbol x_i}\rangle_{\mathcal H_k}=(Pf)(\boldsymbol x_i)
が成り立つ。すなわち、各$\boldsymbol x_i$上での$f$と$Pf$の値は同じである。したがって、この問題を考える上で
f=Pf=\sum_{j=1}^{n}c_j k_{\boldsymbol x_j}
と仮定してよい。(一次関数で表せて嬉しい!!)
f(\boldsymbol x_i)=\langle f,k_{\boldsymbol x_i}\rangle_{\mathcal H_k}=\langle\sum_{j=1}^{n}c_j k_{\boldsymbol x_j},k_{\boldsymbol x_i}\rangle_{\mathcal H_k} =\sum_{j=1}^{n}c_j k(\boldsymbol x_i,\boldsymbol x_j)
は行列を用いると
\begin{pmatrix}
f(\boldsymbol x_1) \\
\vdots \\
f(\boldsymbol x_n)
\end{pmatrix}
=
\begin{pmatrix}
k(\boldsymbol x_1, \boldsymbol x_1) & \cdots & k(\boldsymbol x_1, \boldsymbol x_n) \\
\vdots & \ddots & \vdots \\
k(\boldsymbol x_n, \boldsymbol x_1) & \cdots & k(\boldsymbol x_n, \boldsymbol x_n)
\end{pmatrix}
\begin{pmatrix}
c_1 \\
\vdots \\
c_n
\end{pmatrix}
ここで、$K=(k(\boldsymbol x_i, \boldsymbol x_j)), \boldsymbol c = (c_1, \cdots ,c_n)^T$とおくと$L(f)$は
L(f)=\sum_{j=1}^{n}|f(\boldsymbol x_j)-y_j|^2 = \|K\boldsymbol{c} -\boldsymbol{y} \|_{\mathbb{R}^n}^{2}
と表される。この右辺を最小にするベクトル$\boldsymbol c \in \mathbb{R}^n$を求める問題は通常の線形代数の範囲で解くことができる。実際、$K$に逆行列が存在すれば$\boldsymbol c = K^{-1}\boldsymbol y$とすればよい。
このようにして$\boldsymbol c = (c_1, \cdots , c_n)^T$が求まれば、
f = \sum_{j=1}^{n}c_j k_{\boldsymbol{x}_j} \in \mathcal{H}_k
が問題の解として得られる。
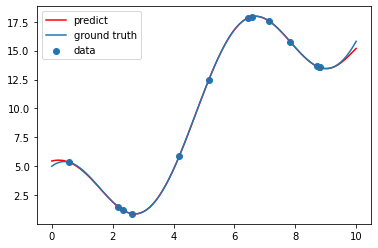
python3での実装例
カーネル関数は様々あるが、この例ではガウスカーネル
k(\boldsymbol{x}, \boldsymbol{y})=\exp(-\gamma\|\boldsymbol{x}-\boldsymbol{y}\|_{\mathbb{R}^d}^{2})
で$\gamma = 0.25$としたものを用いた。
import numpy as np
import matplotlib.pyplot as plt
def kernel(x, y):
return np.exp(-0.5*(x - y)**2 / 2)
def f(x):
return 2 * x + 5 * np.cos(x)
np.random.seed(seed=4)
n = 13
m = 100
X = np.linspace(0, 10, m)
y_truth = f(X)
x = 0.5 + 8.5 * np.random.rand(n)
y = f(x)
K = np.array([[kernel(x[i], x[j]) for j in range(n)] for i in range(n)])
c = np.linalg.inv(K) @ y
y_pred = []
for i in range(m):
sum = 0
for j in range(n):
sum += c[j] * kernel(x[j], X[i])
y_pred.append(sum)
y_pred = np.array(y_pred)
fig, ax = plt.subplots()
ax.scatter(x, y, label="data")
ax.plot(X, y_pred, color="red", label="predict")
ax.plot(X, y_truth, label="ground truth")
ax.legend()
plt.show()