Neo4jことはじめ

Neo4jとは

グラフ構造を持ったデータを扱うことに最適化されたDB（グラフDB）の一種です。
さくっと使ってみます。

インストール

• CentOS 7.2
• JDK 1.8
• Neo4j 3.0.7 （コミュニティ版）

インストールは簡単です。動かすだけなら
https://neo4j.com/download/community-edition/
からtarダウンロード＆展開して

./bin/neo4j start

だけです。
Vagrantとか使っててホストOSからNeo4jのWebインターフェースを利用したいという場合には、conf/neo4j.confの以下の部分をアンコメントすればとりあえず http://localhost:7474 で見た目の綺麗なインタフェースが利用できるので手軽に試してみることができます。

dbms.connector.http.address=0.0.0.0:7474

http://localhost:7474

Cypherの記法

Cypher（サイファー）はグラフの問い合わせ言語、RDBでいうSQLにあたるものです。

• ノードやリレーションのラベルはコロン（:）を前に付けた「:ラベル名」で表現する
• ノードやリレーションのプロパティはJSON形式で表現する
• ノード間のリレーションの向きは矢印（->）で表現する
• ノードやリレーションの作成/削除/変更はCREATE/DELETE/SET
• ノードやリレーションの検索はMATCH

とりあえずこれだけ覚えとけば基本はOK！

↓もっと知りたければここで
Neo4j Cypher Refcard（チートシート）

CRUD例

Cypherの簡単な使用例をいくつか。

名前がTaro、年齢が20のPersonノードを作る

CREATE (:Person{name:"Taro", age:20});

JiroとHanakoの2人をまとめて作る

CREATE
     (:Person{name:"Jiro", age:22}),
     (:Person{name:"Hanako", age:25});

Taroを取得する

MATCH (p:Person{name:"Taro"}) RETURN p;

コロンの前のpはただの変数なのでなんでもOK。
ざっくりいうとname=TaroにマッチしたPersonノードを変数pに入れて返す、という意味。

Taroを削除する

MATCH (p:Person{name:"Taro"}) DELETE p;

TaroからJiroに向けて友達関係を作る

MATCH (p1:Person{name:"Taro"}), (p2:Person{name:"Jiro"}) CREATE (p1)-[:Friend]->(p2) ;

Neo4jのグラフには向きがあるので、TaroはJiroのことを友達だと思っているが逆はそうでもない。

Taro⇒Jiroの友達関係を取得する

MATCH (:Person{name:"Taro"})-[r:Friend]->(:Person{name:"Jiro"}) RETURN r;

Jiro⇒Taroの友達関係を取得する

MATCH (:Person{name:"Taro"})<-[r:Friend]-(:Person{name:"Jiro"}) RETURN r;

JiroはTaroを友達と思っていないので返り値は空。

Jiro⇒TaroもしくはTaro⇒Jisoの友達関係を取得する（方向無視）

MATCH (:Person{name:"Taro"})-[r:Friend]-(:Person{name:"Jiro"}) RETURN r; 

TaroとJiroの間の友達関係を削除する

MATCH (:Person{name:"Taro"})-[r:Friend]->(:Person{name:"Jiro"}) DELETE r;

覚えておくと便利なクエリ

全てのノードを取得。

MATCH (n) RETURN n;

全てのノードとリレーションを削除。

MATCH (n) OPTIONAL MATCH (n)-[r]-() DELETE n, r;

最短経路

ちょっとだけ応用編。
グラフDBといえば必ずセットで出てくる最短経路問題を考えてみます。
A地点からB地点へ行く経路のうち最短のものは？というヤツです。

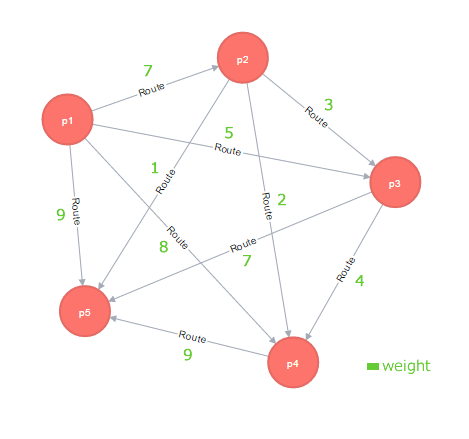
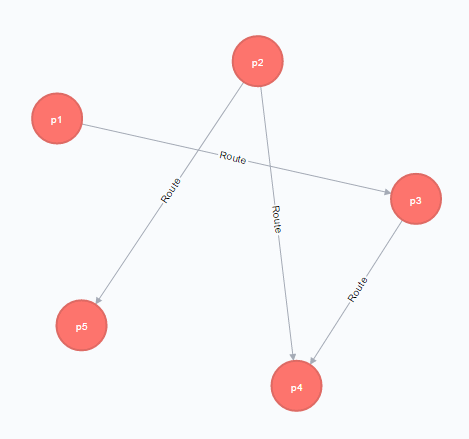
まずサンプルデータとして、p1～p5までの5地点（Pointノード）と各地点から他の地点へのルート（Routeリレーション）を作成します。

CREATE
     (p1:Point{name:"p1"}),
     (p2:Point{name:"p2"}),
     (p3:Point{name:"p3"}),
     (p4:Point{name:"p4"}),
     (p5:Point{name:"p5"}),
     (p1)-[:Route{weight:7}]->(p2),
     (p1)-[:Route{weight:5}]->(p3),
     (p1)-[:Route{weight:8}]->(p4),
     (p1)-[:Route{weight:9}]->(p5),
     (p2)-[:Route{weight:3}]->(p3),
     (p2)-[:Route{weight:2}]->(p4),
     (p2)-[:Route{weight:1}]->(p5),
     (p3)-[:Route{weight:4}]->(p4),
     (p3)-[:Route{weight:7}]->(p5),
     (p4)-[:Route{weight:9}]->(p5);

今回は各地点において他の全ての地点への直通のルートが存在するパターン（完全グラフ）を考えます。各ルートにかかる所要時間の大小はRouteリレーションのweightプロパティで表現し、数値が大きいほど時間がかかるものとします。Neo4jでは向きのない無向グラフは定義できないので各地点を結ぶルートは1方向にのみ作っていますが、あくまで便宜的なものなので意味的には無向と考えてください。

この状態でp1地点からp5地点へ向かう場合を考えます。

p1からp5への最短パスの経路

所要時間（weight）は考えずに単にp1からp5への最短パスを求めるにはshortestPathを使います。

MATCH
     (p1:Point{name:"p1"}),
     (p5:Point{name:"p5"}),
     g = shortestPath((p1)-[:Route*]-(p5))
RETURN g;

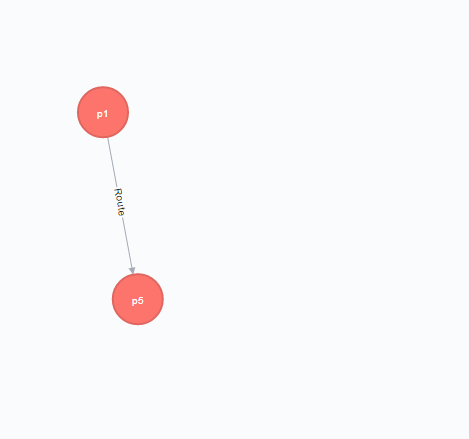
(p1)-[:Route*]-(p5)でp1からp5へ向かう全ての経路が抽出できるので、それをshortestPathに突っ込むと、最も経由するノードの数が少ない経路を取得できます。
この場合はp1から直接p5への向かうルート。

所要時間が最短となるp1からp5への経路

MATCH
     g = (:Point{name:"p1"})-[:Route*]-(:Point{name:"p5"})
RETURN
     g,
     REDUCE(weight=0, r in RELATIONSHIPS(g) | weight+r.weight) AS score
ORDER BY score ASC
LIMIT 1;

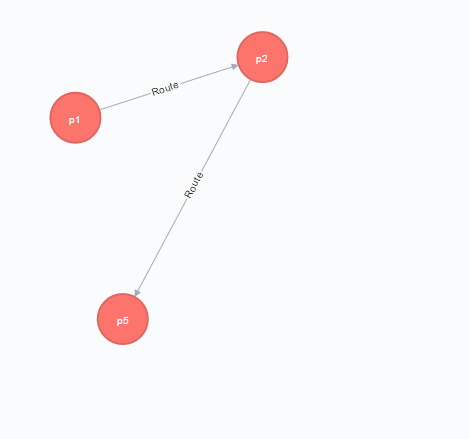
MATCHでp1からp5へ向かう全ての経路を抽出し、REDUCEを使ってそれぞれの経路ごとにweightの値を加算した値を求めまます。
最後にORDER BYとLIMITを使って最小のweightになる経路のみを取得します。
weight=8のp1→p2→p5 が最短になります。

p1から出発し他の地点を全て経由してから最後にp5に到着する最短所要時間の経路

MATCH
     g = (:Point{name:"p1"})-[:Route*4]-(:Point{name:"p5"})
WHERE
     ALL(n IN NODES(g) WHERE SINGLE(m IN NODES(g) WHERE m = n))
RETURN
     g,
     REDUCE(weight=0, r IN RELATIONSHIPS(g) | weight+r.weight) AS score
ORDER BY score ASC
LIMIT 1;

全ての地点に直通のルートがあることから、p1から全ての地点を回ってp5に達するパスの数は必ず4になります。
そこで、MATCH句で[:Route*4]として全ての経路のうち4つのパスを辿る経路のみを抽出します。

ただしこのままでは p1→p5→p3→p2→p5 のように通過しないノードや重複して通過してしまうノードも含まれるので、全てのノードをちょうど1回ずつ通過する経路のみに絞り込む必要があります。

ALLは渡されたリストの中身全てがtrueならtrueを返し、SINGLEはリストの中身のうち1つだけがtrueならtrueを返します。今回はこの2つを使って全てのノード（ALL）について、それぞれのノードが経路リストの中に1つだけ（SINGLE）含まれることを表現し、それをWHERE句の条件として使って全てのノードを1回ずつ通るp1からp5への経路を絞り込んでいます。

具体的には以下の6つの経路です。

• p1 → p2 → p3 → p4 → p5 （weight=23）
• p1 → p2 → p4 → p3 → p5 （weight=20）
• p1 → p3 → p2 → p4 → p5 （weight=19）
• p1 → p3 → p4 → p2 → p5 （weight=12）
• p1 → p4 → p2 → p3 → p5 （weight=20）
• p1 → p4 → p3 → p2 → p5 （weight=16）

あとは同じようにREDUCEでそれぞれの経路のweightの合計値を求め最短所要時間の経路のみを取得します。
weight=12のp1→p3→p4→p2→p5 が最短になります。

参考

グラフデータベース ―Neo4jによるグラフデータモデルとグラフデータベース入門