円周率の近似値の計算方法
1. (1×1)の正方形のマスにランダムに点を打つ。
2. 計N回繰り返す。
3. 原点からの距離が1以下である確率が π/4 に近づく
4. つまり(原点からの距離が1以下である確率)×4がπに近づく
モンテカルロ法をpythonで実行するとこのようになります。
monte.py
import math
import numpy as np
import matplotlib.pyplot as plt
x_all=[]
y_all=[]
pi = []
pi_mean = []
count=[]
N = 100
for i in range(1000):
count.append(i)
for i in range(N):
incount = 0
allcount = 0
x = np.random.rand()
y = np.random.rand()
x_all.append(x)
y_all.append(y)
if x ** 2 + y ** 2 < 1:
incount += 1
allcount += 1
pi.append(4 * incount / allcount)
pi_mean.append(np.mean(pi))
plt.plot(count,pi_mean)
plt.axhline(y=math.pi, color='red')
plt.show()
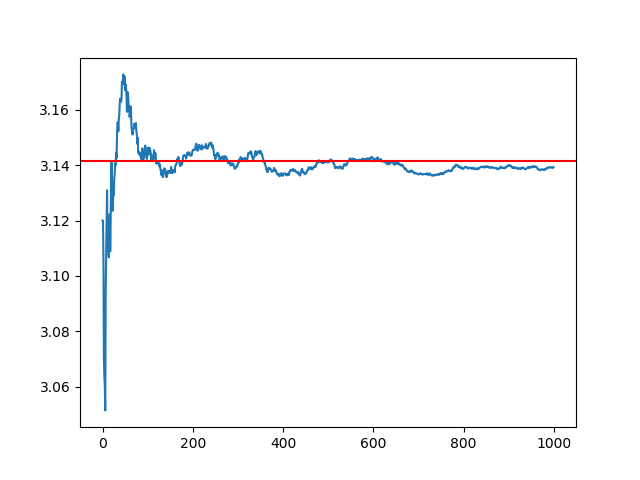
以下は試行回数100回を1000セットやった時に計算された円周率の平均の結果になります。
これを見てわかる通り、だいたいモンテカルロ法で計算された円周率がだいたい近似できていると言えます。