概要
何よりも大きい数の話をしよう。
ここでは巨大数を作るツールとして有用な急増加関数と、
急増加関数を扱う上で必須な順序数の話をします。
理解している範囲までなので幾分適当な説明があるかもしれない。
急増加関数
急増加関数: $f_{\alpha}(n)$は2変数関数で$\alpha$に順序数、$n$に自然数をとり、自然数を返す。
まずは基本の2ルールを理解しよう。
- $\alpha=0$のとき, $f_0(n)=n+1$
- $f_{\alpha+1}(n)=f_{\alpha}^n(n)$
順序数というのは$0, 1, 2, \dots$と無限に続く列で
$\alpha=0$のときは1を足すただの後者関数。
2つ目のルールは$\alpha$が1増えるとその前の関数を$n$重にするというもの。
この性質が関数を急増加させるものとなり、
$\alpha=1,2,3,4$のとき、それぞれ加算、乗算、冪乗、テトレーションの強さを持つ関数になる。
模式的に書くならこう。
def f(o: int, n: int) -> int: # 急増加関数
if o = 0:
return n + 1
new_o = o - 1
k = f(new_o, n)
for i in range(n - 1):
k = f(new_o, k)
return k
ただし、$o=4$とかで既にまともに計算できない。
小さな$n$ですら桁数が宇宙の粒子数を超えてしまうので当然といえば当然。
なにせ$f_3(3)=(24*2^{24})2^{(242^{24})}$
自然数を超えた順序数
さて、順序数は自然数を超えた先にも続いていく。
自然数全体を数え終わったとしてその個数を$\omega$と定義すると、
$\omega,\omega+1,\omega+2,\dots $とまた自然数を数えることができる。
有限でない順序数を超限順序数といい、
$\omega$は有限でない最小の順序数である。
順序数の恐ろしさはここから始まる。
後続順序数と極限順序数
ここで用語の定義。
$\omega+1$のように前の順序数が存在する順序数を後続順序数という。
0でも後続順序数でない順序数を極限順序数という。
$\omega$は最小の極限順序数で、その次は$\omega+\omega$で$\omega2$と書く。その次は$\omega3$。
$\omegan$と書けない最小の極限順序数は$\omega\omega$で$\omega^2$と書く。
順序数は降順の多項式で書く。
$1+\omega$と書くと$1$を数えてから$\omega$を数えると$\omega$になってしまい、これは$\omega+1$とは異なる。
なので例えば、$w^{w^2}+w^55+w^22+w+2$のように書く。
超限順序数に対する急増加関数
急増加関数に$\omega$を入れるとどうなるのだろう。
実は$\omega$がもう一つの引数に変わる。$f_{\omega}(n)=f_n(n)$となる。
たとえば$f_{\omega}(6)=f_6(6)$
より正確に書くと$\alpha$が極限順序数のとき、急増加関数には1つのルールが加わる。
- $f_{\alpha}(n)=f_{\alpha [n]}(n)$ ただし$\alpha [n]$は極限順序数$\alpha$の収束列の$n$番目
$\alpha$が後続順序数のとき、順序数を$1$減らして関数を$n$重にするというルールは健在である。
すなわち$f_{\omega+1}(3)=f_\omega(f_\omega(f_\omega(3)))=f_\omega(f_\omega((24*2^{24})2^{(242^{24})}))$
たとえ$n$が小さな値でも1個目の$\omega$を外した時点で爆発して2個目の$\omega$から先は計算できなくなる。
$f_{\omega+1}(64)$でおよそグラハム数になる。関数の入れ子恐ろしい。
極限順序数の収束列
実際にいくつかの極限順序数に対して急増加関数を展開しながら収束列を考えてみる。
数式装飾は大変なのでここからは急増加関数をテキストライクな関数で記述する。
ω
wの収束列は1,2,3, なのでwに3を入れるだけ
f(w,3)=f(3,3)
ω*k
w2の収束列はw+1,w+2,w+3,
f(w2,3)=f(w+3,3)=f(w+2,f(w+2,f(w+1,f(w+1,f(w,f(w,f(3,3))))))))
w+3は後続順序数なので関数を3重にして展開していくと結局同じ関数が2個ずつ並ぶ形になる。
w3の収束列はw2+1,w2+2,w2+3,
f(w3,3)=f(w2+3,3)=f(w2+2,f(w2+2,f(w2+1,f(w2+1,f(w2,f(w2,f(w+3,3))))))))
w2はw+kが増殖している。w3はw*2+kが増殖していることがおわかりだろうか。
ω^k
w2の収束列はw,w2,w3,
f(w^2,3)=f(ww,3)=f(w3,3)
なんだ2乗はf(w3,3)と同じじゃないかと思うかもしれないがf(w^2,100)ならf(w100,100)になるわけだし、
f(w^2+1,3)=f(w^2,f(w^2,f(w3,3)))だから乗算とは次元が異なる。
w3の収束列はw^2,w^22,w^23,
f(w^3,3)=f(w^2w,3)=f(w^23,3)=f(w^22+w^2,3)=f(w^22+ww,3)=f(w^22+w3,3)=f(w^22+w2+3,3)
3乗を展開すると2乗とwになり、そこから3倍を2倍と1倍の多項式に分け、小さい1倍の方をさらに展開していきます。
w^22+w3のような多項式は末端のw*3を減らすように計算していき、末端が0にならないと次の項は減らせません。
ω^(w+k)
w^wの収束列はw,w^2,w^3,
f(w^w,3)=f(w^3,3)
w^wkの収束列はw^w(k-1)+w,w^w*(k-1)+w^2,w^w*(k-1)+w^3,
f(w^wk,3)=f(w^w(k-1)+w^w,3)=f(w^w*(k-1)+w^3,3)
w^(w+1)の収束列はw^w,w^w2,w^w3,
f(w^(w+1),3)=f(w^ww,3)=f(w^w3,3)=f(w^w2+w^w,3)=f(w^w2+w^3,3)
w^(w+2)の収束列はw^(w+1),w^(w+1)*2,w^(w+1)*3,
f(w^(w+2),3)=f(w^(w+1)*w,3)=f(w^(w+1)*3,3)=f(w^(w+1)*2+w^(w+1),3)=f(w^(w+1)2+w^w3,3)
ω^(w*k)
w^(w2)の収束列はw^(w+1),w^(w+2),w^(w+3),
f(w^(w2),3)=f(w^(w+w),3)=f(w^(w+3),3)=f(w^(w+2)*w,3)=f(w^(w+2)*3,3)=f(w^(w+2)*2+w^(w+2),3)
=f(w^(w+2)*2+w^(w+1)*2+w^w*2+w^3,3)
ω^w^k
w^w^2の収束列はw^w, w^(w2),w^(w3),
f(w^w^2,3)=f(w^(ww),3)=f(w^(w3),3)
w^w^3の収束列はw^w^2, w^(w^22),w^(w^23),
f(w^w^3,3)=f(w^(w^2w),3)=f(w^(w^23),3)=f(w^(w^22+w^2),3)=f(w^(w^22+ww),3)=f(w^(w^22+w3),3)
=f(w^(w^22+w2+3),3)=f(w^(w^22+w2+2)*w,3)=f(w^(w^22+w2+2)*3,3)
=f(w^(w^22+w2+2)*2 + w^(w^22+w2+2),3)
=f(w^(w^22+w2+2)*2 + w^(w^22+w2+1)*2 + w^(w^22+w2)*2+ w^(w^22+w+3),3)
2重指数の肩が3になってから急に複雑になっている。どうなっているのだろうか。
指数の肩の上で順序数の多項式が展開されることが繰り返されている。
すると指数の末端がいつかは自然数になり、そこを1減らす代わりに指数の外側に$\omega$を出すことができる。
w^w^w^w
w^w^w^wの収束列はw^w^w,w^w^w^2,w^w^w^3,
f(w^w^w^w,3)=f(w^w^w^3,3)=f(w^w^(w^2*w),3)=f(w^w^(w^2*3),3)=f(w^w^(w^2*2+w^2),3)
=f(w^w^(w^2*2+ww),3)=f(w^w^(w^2*2+w3),3)=f(w^w^(w^2*2+w2+w),3)=f(w^w^(w^2*2+w2+3),3)
=f(w^(w^(w^2*2+w2+2)*w),3)=f(w^(w^(w^2*2+w2+2)*3),3)
=f(w^(w^(w^2*2+w2+2)*2+w^(w^2*2+w2+1)*w),3)
=f(w^(w^(w^2*2+w2+2)*2+w^(w^2*2+w2+1)*3),3)
=f(w^(w^(w^2*2+w2+2)*2+w^(w^2*2+w2+1)*2+w^(w^2*2+w2+1)),3)
=f(w^(w^(w^2*2+w2+2)*2+w^(w^2*2+w2+1)*2+w^(w^2*2+w2)*2+w^(w^2*2+w+3)),3)
ううむw^(w^2*2+w+3)の展開はなかなか終わる気がしない。
一番外側の指数にwを1回落とすことすら叶わなかった。
ωの果てのε0
ε0の収束列はw,w^w,w^w^w,
wの冪乗の果てにあるのが$\epsilon_0$である。
ここから先は$\psi$関数を用いて$\psi(0,0)=\omega, \psi(1,0)=\epsilon_0, \psi(2,0)=\eta_0$,とする方がわかりやすいが、
$\epsilon_0$ から $\eta_0$の果てしなさを見ておこう。
ε1への道
e_0の次の順序数はe_0+1
f(e_0+1,3)=f(e_0,f(e_0.f(e_0,3)))=f(e_0,f(e_0.f(w^w^w,3)))
e_0の次の極限順序数はe_0+w
e_02=e_0+e_0で収束列はe_0+w,e_0+w^w,e_0+w^w^w,
e_0wの収束列はe_0,e_02,e_03,
e_0^2=e_0e_0の収束列はe_0w,e_0w^w,e_0w^w^w,
e_0^wの収束列はe_0.e_0^2,e_0^3,
e_0^w^2=e_0^(ww)の収束列はe_0^w,e_0^(w2),e_0^(w*3),
e_0^e_0の収束列はe_0^w,e_0^w^w,e_0^w^w^w,
e_1の収束列はe_0,e_0^e_0,e_0^e_0^e_0,なのだが、
e_0+1,w^(e_0+1),w^w^(e_0+1),としても同じで、後々のことを考えるとこちらの方が都合が良い。
e_1はe_0以下の数とそれまでに登場した演算を繰り返しても到達できない数のことであり、
eの世界で許されている最高の演算は冪乗なので
w^w^w^...の指数タワーのてっぺんにe_0を入れたのがe_1ということになる。
1を足している理由は私には説明できないが、巨大数ではよくあること。
ε_ε1への道
$\epsilon_0,\epsilon_1,\epsilon_2, \dots$の収束先は当然$\epsilon_{\omega}$である。
そこから$\epsilon_w,\epsilon_{w2},\epsilon_{w3}, \dots$の収束先は$\epsilon_{(\omega^2)}$
$\epsilon_w,\epsilon_{w^2},\epsilon_{w^3}, \dots$の収束先は$\epsilon_{(\omega^\omega)}$
$\epsilon_w,\epsilon_{w^w},\epsilon_{w^{w^w}}, \dots$の収束先がやっと$\epsilon_{\epsilon_0}$になる。
ここまででも大変だがeの2個目を1増やすのはどれだけ大変なのだろう。
まずw^w^w^...^$\epsilon_{\epsilon_0+1}$はどうなるだろうか。
これは$\epsilon$の1個目を1増やすので$\epsilon_{\epsilon_0+1}$になる。
そして$\epsilon_0$からここまでのことを繰り返したとしても
$\epsilon_{\epsilon_0+\epsilon_0}=\epsilon_{\epsilon_0 * 2}$にしかならない。
$\epsilon_{\epsilon_1}$にするには*2となっている部分を$\epsilon$の指数タワーにしないといけない。
εの果てとηの世界
$\epsilon$の2個目を増やすことは大変だが、その極限までいくと$\epsilon_{\epsilon_{\epsilon_0}}$まで行けそうだ。
では$\epsilon_0,\epsilon_{\epsilon_0},\epsilon_{\epsilon_{\epsilon_0}},\dots$の極限はというと、
それが次の区切りとなる$\psi(2,0)=\eta_0$である。
$\eta_1$とは$\eta_0$とそれ以下の演算では到達できない数のことなので、
$\eta_1 \neq {\eta_0}^{{\eta_0}^{\eta_0}\dots}$
$\eta$の世界での最高の演算は$\omega$の冪乗を連鎖させることではなく,
$\epsilon$の連鎖なので、
$\eta_1=\epsilon_{\epsilon_{\epsilon \dots} \eta_0}$となる。
ヴェブレン関数
ψ関数
$\eta_1$を ウェブレンの$\psi$関数で書いてみよう。
$\eta_1=\psi(2,1)=\psi(1,\psi(1,\psi(1,\dots \psi(1,\psi(2,0))\dots)))$
$\epsilon$の入れ子の一番奥に$\eta_0$を入れたものになっている。
これを一般化すると
$\psi(n+1,m+1)=\psi(n,\psi(n,\psi(n,\dots \psi(n,\psi(n+1,m))\dots)))$
と書ける。
これで(右から数えて)1つ目の引数を1つ増やすルールは記述できた。
では2つ目の引数を1増やすにはどうすればよいのだろう。
それは1つ目の引数を極限まで大きくすることを考えると、自身を入れ子にすればよくて、
$\psi(n+1,0)=\psi(n,\psi(n,\psi(n,\dots \psi(n,\psi(n,0))\dots)))$
となる。
ψ関数の展開
試しに$\psi(4,2)$あたりを急増加関数に入れてみよう。
$f(\psi(4,2),3)=f(\psi(3,\psi(3,\psi(4,1)))),3)=f(\psi(3,\psi(3,\psi(3,\psi(3,\psi(4,0))))))),3)$
$=f(\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,0)))))))))),3)$
$=f(\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(2,\psi(2,\psi(2,0)))))))))))),3)$
$=f(\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(2,\psi(2,\psi(1,\psi(1,\psi(1,0)))))))))))))),3)$
$=f(\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(2,\psi(2,\psi(1,\psi(1,\omega^{\omega^\omega}))))))))))))),3)$
$=f(\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(3,\psi(2,\psi(2,\psi(1,\psi(1,\omega^{\omega^2 2+\omega3}))))))))))))),3)$
$\psi(1,0)$まで行けば$\omega$の指数タワーに落とせるが……
フェファーマン・シュッテの順序数
$\psi(1,0),\psi(2,0),\psi(3,0) ,\dots$の収束先は$\psi(\omega,0)$だが、もちろんこれが限界ではない。
2つ目の引数を極限まで大きくすることを考えると
$\psi(\psi(\psi(\dots \psi(\psi(1,0),0)\dots,0),0),0)$
が限界で、これをフェファーマン・シュッテの順序数といい、
$\psi(1,0,0)=\Gamma_0$
と書く。
$\psi(1,0,1)=\Gamma_1$は$\Gamma_0$と二変数$\psi$関数で表せない最小の数なので、
$\psi(1,0,1)=\psi(\psi(\psi(\dots \psi(\psi(1,0,0),0)\dots,0),0),0)$
$\psi(1,0,k+1)=\psi(\psi(\psi(\dots \psi(\psi(1,0,k),0)\dots,0),0),0)$
2つ目の変数を1つ増やすには1つ目に入れ子にする
$\psi(1,k+1,0)=\psi(1,k,\psi(1,k,\psi(\dots \psi(1,k,\psi(1,k,0))\dots)))$
3つ目の変数を1つ増やすには2つ目に入れ子にする
$\psi(k+1,0,0)=\psi(k,\psi(k,\psi(\dots \psi(k,\psi(k,0,0),0)\dots),0),0)$
3つ目に入れ子にすると4変数になる
$\psi(1,0,0,0)=\psi(\psi(\psi(\dots \psi(\psi(1,0,0),0,0)\dots),0,0),0,0)$
$\psi(1,0,0,0)$と3変数$\psi$関数で到達できないのが次の4変数のやつなので
$\psi(1,0,0,1)=\psi(\psi(\psi(\dots \psi(\psi(1,0,0,0),0,0)\dots),0,0),0,0)$
以降はk+1つ目の変数を1つ増やすにはkつ目に入れ子にすると、
変数がk個のときにkつ目に入れ子にするとk+1変数になるを繰り返せば良い。
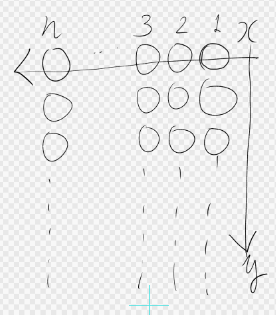
この階層のイメージ
この階層の果てしなさをランプの点灯でイメージしてみよう。
右上を原点として$x$方向は$n$個、$y$方向には$\omega$個のランプが並んでいる図を想像してみよう。
1列目のランプを1つ点けるには$x$のサイズが$n-1$の別の表を用意し、これが全て点灯した時に1つ点けることができる。
1列目を全て点灯させると1列目を全て消して2列目を1つ点灯させることができる。
2列目を全て点灯させると2列目を全て消して3列目を1つ点灯させることができる。
n列目を全て点灯させると$x$のサイズが$n+1$の新しい表に移って1列目のランプを1つ点ける。
この新しい表の2個目のランプを点けるには先程の$x$のサイズ$n$の表をもう一度全て点灯させる必要がある。
ヴェブレン関数の限界
小ヴェブレン順序数
$\psi$関数の変数の個数が$\omega$個になった順序数である。
さらにその先の順序数
小ヴェブレン順序数の変数の数が超限的になる大ヴェブレン順序数。
バッハマン・ハワード順序数、竹内・フェファーマン・ブーフホルツ順序数と続く。
これらを理解するには順序数崩壊関数が必要となる。