2標本の差の検定のために前提条件を確認すべき？（標本が正規分布に従うとき）

目次

●段階的検定とは？
●検定のしくみ
●現実には
●いくつかの2標本の差の検定の比較
●段階的検定の標本の大きさとσを変えたとき
●段階的検定の標本の大きさの比とσを変えたとき
●Welchの検定とMann-Whitneyの検定による段階的検定
●結論

段階的検定とは？

　はじめに，段階的検定という統計用語はありません．本記事の造語です．本記事でいう段階的検定とは，例えばデータが正規分布に従うかを統計的検定（以下，検定）で確認して，正規分布に従うなら（正確には，従わないといえないなら）○○検定，従わないなら××検定，というようにいくつかの検定を段階的に行って最終的な検定を決めることです．
　医療系の研究では，事前にいくつか検定を行って，データが検定の前提条件を満たすかを確認する段階的検定が非常に多い．というか，ほとんどこれです．この手順の問題については，多くの指摘があります→ここ1　ここ2
　異口同音で「段階的検定はダメ！」と述べてあります．まさにその通り．

検定のしくみ

　はじめに，2標本の平均の差の検定を例に挙げて，検定のしくみを断っておきます．例えば，
$X_1,…,X_m～N(\mu_x，\sigma_x)，Y_1,…,Y_n～N(\mu_y，\sigma_y)　(i.i.d.)$
の2標本があり，帰無仮説$H_0：\mu_x=\mu_y$を立てます．母分散未知かつ等しい場合は2標本$t$検定を適用します．
　このとき，検定の対象となるのは帰無仮説$H_0：\mu_x=\mu_y$だけであり，その他の仮説は対象にしません．それぞれ$N(\mu_x，\sigma_x)，N(\mu_y，\sigma_y)$からの標本であることが前提なので，改めてこれを確認する意味も必要もありません．
　それをわざわざ事前に確認するのは，ばかげています．これが統計的検定の理論的な主張です．
　ということは，ある検定の結果をみてから「次は，この検定を…」という選択はあり得ないのです．

現実には

　しかし現実には$N(\mu_x，\sigma_x)，N(\mu_y，\sigma_y)$からの標本かどうかはわかりません．
　統計解析に慣れない人は「母分散が等しい場合は2標本$t$検定を適用」といわれると「等しいという根拠は？」と常に考えてしまいます．ゆえに「等分散性の検定でp<0.05ならば$Welch$の検定を…」と判断せざるを得ません．これに理論家は「理論的におかしい．間違っている」と指摘します．何も知らない人は恐縮してしまい「この本には，そうしろと書いてるのに，統計学者に間違っているといわれた…」と悩みます．
　そこで「ではどうすればよいでしょうか？」と聞いてみると，「最初から2標$t$検定を適用すればよいのだ．前提条件を検定で確認してはならない」との返答を得ます．よく考えると，間違いの指摘はされていますが，この返答では論点が異なります．仮に「こうしたらいいのですよ！」といわれたとしても，それが正解である保証は，全くありません．正解はだれもわからないのです．よく考えてみて下さい．権威あるお方が「こうしろ！」といった内容が理論ではなく現実にも正解なら，こんな長い期間，検定の問題を引きずるわけがありません．アインシュタインとニールス・ボーア，フィッシャーとピアソンの論争にも表れていますが，いまだに理論と現実の対立は決着がついていません．
　ゆえに，”間違いをわきまえたうえで¹，いまは最善の（慣習的な）方法であるが，今後，研究によって理論体系が変わる可能性はある．ゆえに検定結果に依存した判断は，将来，多くの犠牲を伴うリスクも考慮して慎重に解釈すべき”という立場で解析するように薦めます．

いくつかの2標本の差の検定の比較

　シミュレーションも理論疑似乱数を使用しますので理論の話になります．現実とは程遠いとまではいいませんが，一つの根拠になるかもしれません．
　まずは，正規分布に従うか否か，等分散性が成り立つかどうかは無視して，正規分布に従う2標本のデータに対して，

• 2標本$t$検定
• $Welch$の検定
• $Mann-Whitney$の検定

を適用します．以降のシミュレーションの有意水準は$p=0.05$とします．

シミュレーションの手順

　シミュレーションは，$1-\alpha$，検出力（$1-\beta$）の2通り行います．$1-\alpha$は，個人の好みで$\alpha$を算出します．

①乱数の発生

　R4.2.3を使用します．
　$X_1,…,X_n～N(0，1.0)，Y_1,…,Y_m～N(0，\sigma_y)$の正規乱数を発生させます．以下の各条件とします．
　$n：m=10：10，20，30，50$（4通り）
　$\sigma_x：\sigma_y＝1.0：1.0，1.1，1.2，1.3，1.4，1.5$（6通り）
に変化させます．検出力では，$\mu_y=1.5$とします．
$XとY$をvariable列，$X＝0，Y＝1$としたgroup列（as.factor）のdataを作成します．

②検定の手順

dataに対して，2標本の差の検定を行います．
（１）$X，Y$に対して，2標本$t$検定
t.test(variable~groups, alternative='two.sided', conf.level=.95, var.equal=TRUE, data=data)
を行います．→p値を回収
（２）$X，Y$に対して，$Welch$の修正による2標本t検定
t.test(variable~groups, alternative='two.sided', conf.level=.95, var.equal=FALSE, data=data)
を行います．→p値を回収
（３）$X，Y$に対して，$Mann-Whitney$の検定
wilcox.exact(variable~groups,data,paired=F)を行います．→p値を回収
　これらを，各10,000回繰り返し計算します．$p<0.05$の数を数え，割合を求めます．10,000回検定して500回分，5％（＝0.05）の$\alpha$エラーが理想です．検出力では，1に近づくほど良いと判断します．

αエラーの結果

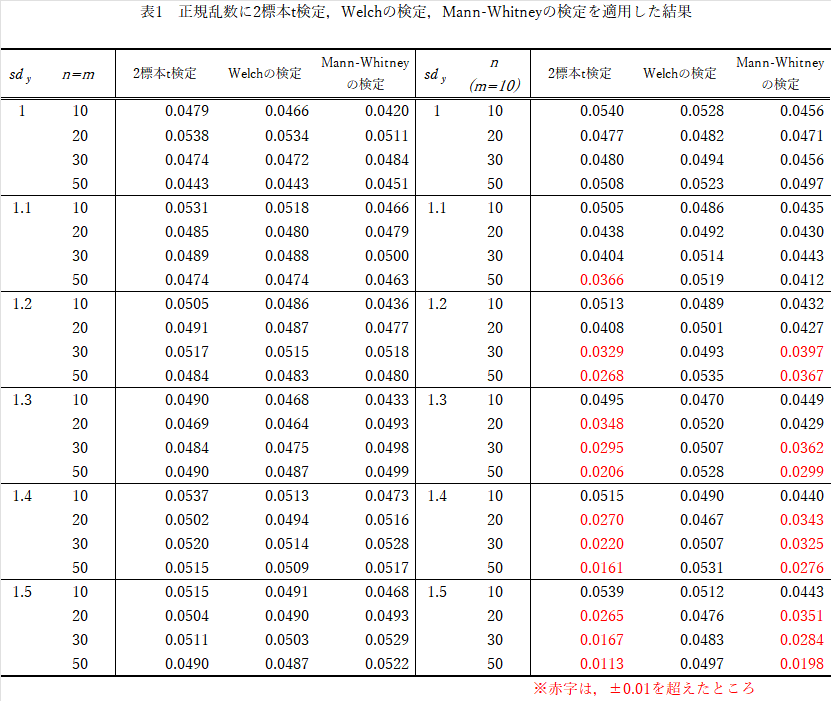
結果（表1）の要約

• $n=m$では，$\sigma_x：\sigma_y$を変えようが，$n：m$を変えようが，どの検定もほぼ違いはない．
  • そもそも2標本$t$検定，$Mann-Whitney$の検定は，$\sigma_x：\sigma_y＝1：1$でなければならないが．
• $n \neq m$では，$Welch$の検定以外は$\sigma_x：\sigma_y$の比，$n：m$の比が違い過ぎるほど保守的になる（有意差が出にくい）．

　$n=m$なら等分散性は気にしなくて良いでしょうが，現実に$n \neq m$の場合が多いでしょう．事前に等分散性を確認する手順は必要と思います．

検出力（1-β）の結果

　$\mu_x=0，\mu_y=1.5$でシミュレーションしています．

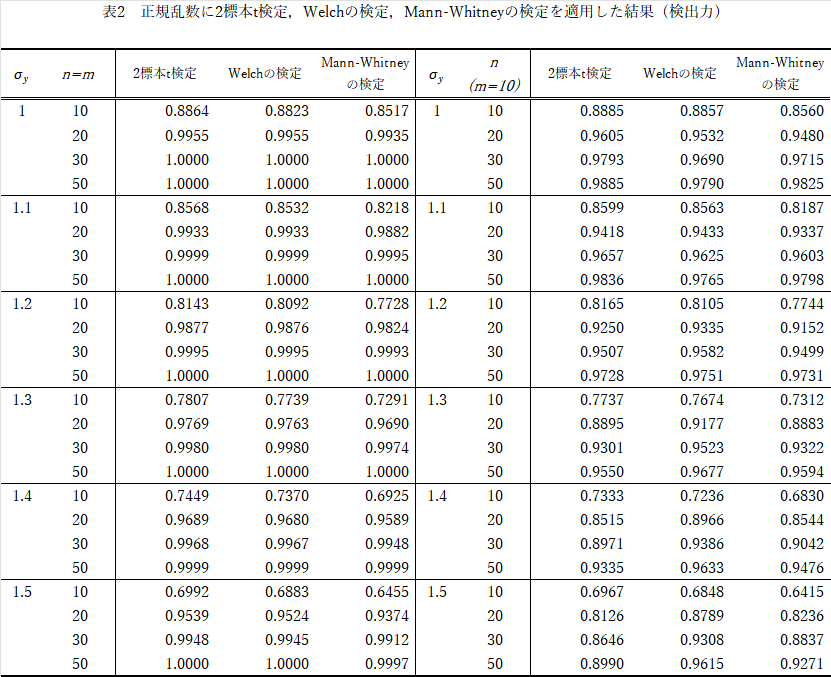
結果（表2）の要約

• $n=m$の検出力は2標本$t$検定＞$Welch$の検定＞$Mann-Whitney$の検定の順で，$\sigma_x：\sigma_y$の比が異なるほどこの傾向は強くなり，全体に検出力が下がります．
• $n \neq m$では，$n：m$の比が異なるほど検出力は上がり，さらに$\sigma_x：\sigma_y$の比が異なるほど検出力は下がります．$Welch$の検定では，この傾向はわずかです．やはり不等分散性には強い．

　2標本の大きさはできる限り揃えた方が理論に従います．$\sigma$のアンバランスには，当然ながら$Welch$の検定が妥当です．

段階的検定の標本の大きさとσを変えたとき

　それでは，段階的検定で確認します．

シミュレーションの手順

①乱数の発生

　$X_1,…,X_n～N(0，1.0)，Y_1,…,Y_m～N(0，\sigma_y)$の正規乱数を発生させます．以下の各条件とします．
　$n：m=10：10，20，30，50$（4通り）
　$\sigma_x：\sigma_y＝1.0：1.0，1.1，1.2，1.3，1.4，1.5$（6通り）
に変化させます．検出力では，$\mu_y=1.5$とします．
$XとY$をvariable列，$X＝0，Y＝1$としたgroup列（as.factor）のdataを作成します．

②検定の手順

2標本の差の検定を行います．そのために以下の段階的検定を行います．
（１）$X，Y$に対して，$Shapiro-Wilk$の検定
c(tapply(variable,group, shapiro.test)
を適用します．少なくとも一方がp<0.05のときは（５）へ，それ以外は（２）へ進みます．
　なお，$Shapiro-Wilk$の検定は，$X，Y$に対して2回行うのでp値を$Holm$修正した場合でも行います．
（２）$X，Y$に対して，$Levene$の検定
leveneTest(variable,group,center=mean)
を適用します．結果がp<0.05のときは（４）へ，それ以外は（３）へ進みます．
　$Levene$の検定で$p=0.05以外に，p=0.1，0.2$とした場合でも行います．
（３）$X，Y$に対して，2標本t検定
t.test(variable~groups, alternative='two.sided', conf.level=.95, var.equal=TRUE, data=data)
を行います．→p値を回収
（４）$X，Y$に対して，$Welch$の検定
t.test(variable~groups, alternative='two.sided', conf.level=.95, var.equal=FALSE, data=data)
を行います．→p値を回収
（５）$X，Y$に対して，$Mann-Whitney$の修正による2標本t検定
wilcox.exact(variable~groups,data,paired=F)
を行います．→p値を回収
①の各条件で，さらに$Shapiro-Wilk$の検定をHolm修正した場合（2通り）と，$Levene$の検定で$p=0.05，0.1，0.2$とした場合（3通り），②の手順を各10,000回ずつ繰り返します．有意水準はp=0.05とします．

αエラーの結果

　　以上の結果です．0.05（5％）が理論値です．これに近いほど良い（理論通り）といえます．
　$Shapiro-Wilk$の検定では，通常の方法（normal）とp値を$Holm$修正した場合（Holm's adjust p）の表示となっています．　

　
　$Levene$の検定は，$p<0.05$ではなく，次に続く検定の$\alpha=0.05×4～5$倍が望ましい，という意見もあるので，$0.05$から$0.1，0.2$と変化させたシミュレーションも行っています．

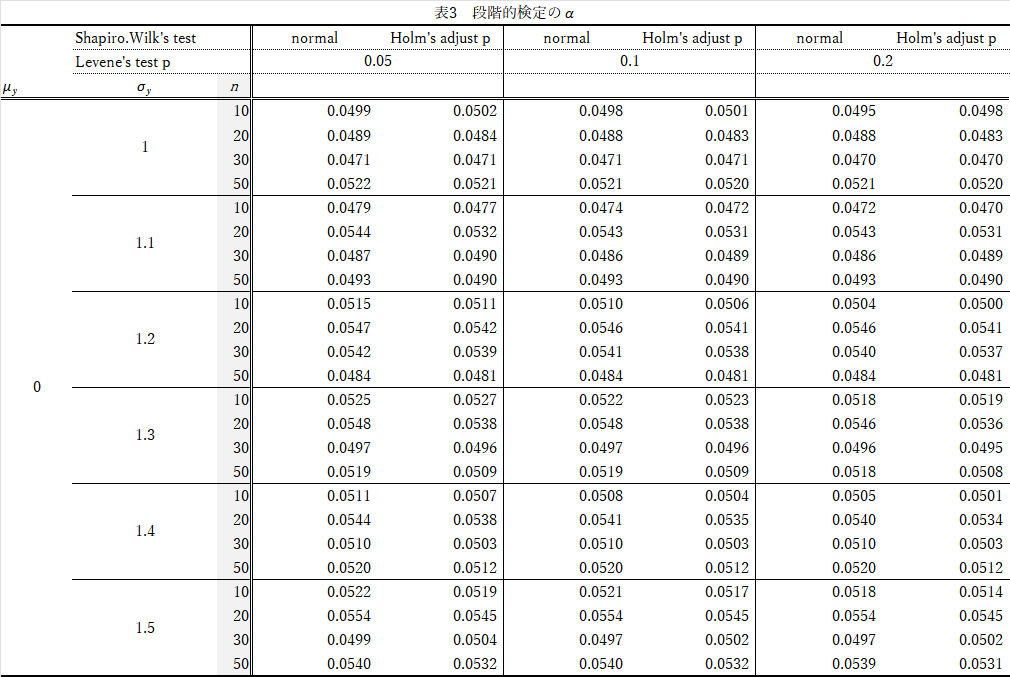
結果（表3）の要約

• $Shapiro-Wilk$の検定で，$Holm$修正しても，しなくてもほぼ差なし．
• $n$の大きさを変えても大差なし．
• $Levene$の検定の有意水準を変えてもほぼ差なし（ごくわずかに0.05を超える傾向=有意差が出やすい）
• $X，Y$の$\sigma$が異なるほど（$\sigma_y$が1→1.5）と，0.05よりやや大きな方向（0.05を超える傾向=有意差が出やすい）に偏るが，現実には問題ないレベル．

検出力（1-β）の結果

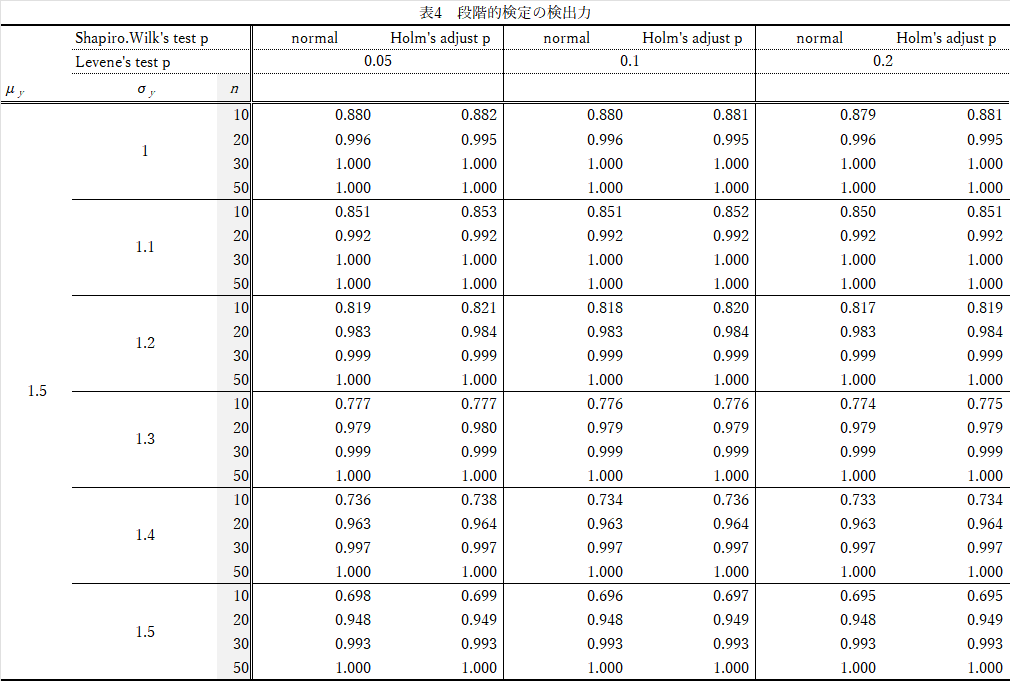
結果（表4）の要約

• $Shapiro-Wilk$の検定で，$Holm$修正した方が，ごくわずかに検出力は高い．
• $n$が大きいほど検出力は高い（当然だが）
• $Levene$の検定の有意水準を変えても大差なし（有意水準を上げると0.05→0.2，やや検出力が下がる）
• $X，Y$の$\sigma$の比が異なる（$\sigma_y$が1→1.5）と，検出力は下がる．．

　全般に，表2よりも検出力は，やや高くなります．

段階的検定の標本の大きさの比とσを変えたとき

　
　Behrens-Fisher問題は，標本の大きさの比に影響を受けます．
　$n＝10$を固定する以外は，上記と同様です．

αエラーの結果

　以下が結果です．理想は0.05（5％）です．

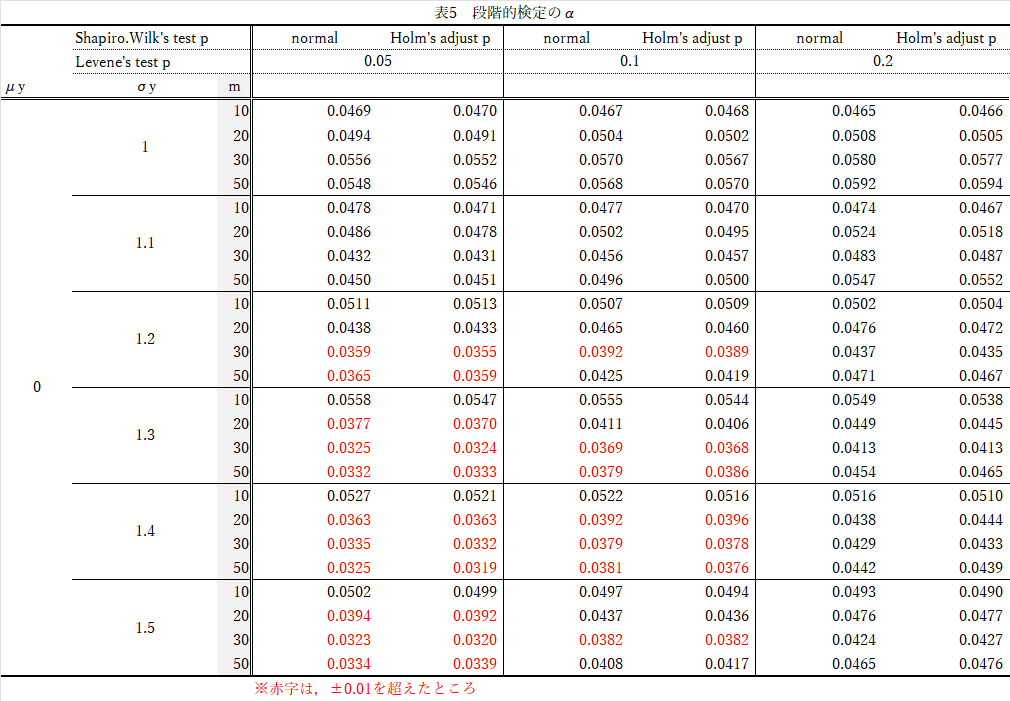
結果（表5）の要約

• $Shapiro-Wilk$の検定で，$Holm$修正しても，しなくてもほぼ差なし．
• $n:m$の比が異なるほど，$X，Y$の$\sigma$の比が異なるほど，0.05を下回る（=有意差が出にくい）．$Levene$の検定で$p=0.2$にするとその傾向は小さい．
• $X，Y$の$\sigma$が異なるほど（$\sigma_y$が1→1.5）と，0.05より小さい方向（=有意差が出にくい）に偏る．

検出力（1-β）の結果

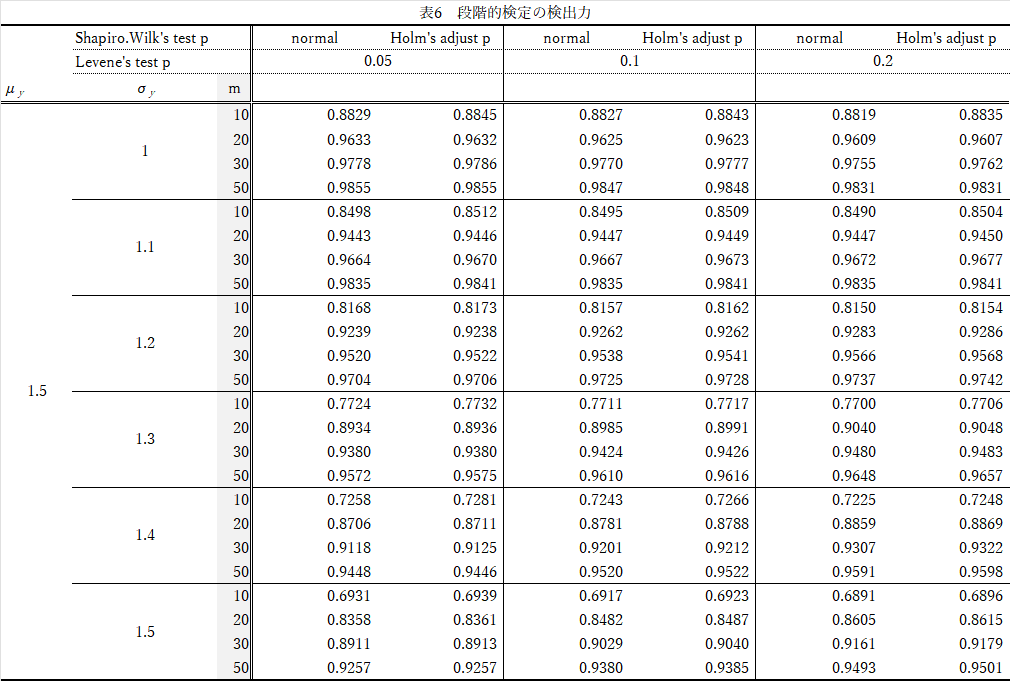
結果（表6）の要約

• $Shapiro-Wilk$の検定で，$Holm$修正した方が，わずかに検出力は高い．
• $n$が大きいほど検出力は高い（当然）
• $Levene$の検定の有意水準を変えても大差なし（やや検出力が上がる）
• $X，Y$の$\sigma$の比が異なると，検出力は下がる．
• 全般に，$n=m$と比較して検出力は低い．

Welchの検定とMann-Whitneyの検定による段階的検定

　追加で，以下の方法で段階的検定を行ってみます．
　正規分布に従う2標本の差の検定では，等分散性の確認のために$Levene$検定を行わず，常に$Welch$の検定を行えばよい，という意見もあります．それも段階的検定で確認します．

シミュレーションの手順

①乱数の発生

　上述の方法と同様です．$n=m$，$n \neq m$の2通りで行います．

②検定の手順

2標本の差の検定を，以下の段階的検定で行います．
（１）$X，Y$に対して，$Shapiro-Wilk$の検定
c(tapply(variable,group, shapiro.test)
を適用します．少なくとも一方がp<0.05のときは（３）へ，それ以外は（２）へ進みます．
　なお，$Shapiro-Wilk$の検定は，$X，Y$に対して2回行うのでp値を$Holm$修正した場合でも行います．
（２）$X，Y$に対して，$Welch$の検定
t.test(variable~groups, alternative='two.sided', conf.level=.95, var.equal=FALSE, data=data)
を行います．→p値を回収
（３）$X，Y$に対して，$Mann-Whitney$の修正による2標本t検定
wilcox.exact(variable~groups,data,paired=F)
を行います．→p値を回収
①の各条件で，さらに$Shapiro-Wilk$の検定をHolm修正した場合（2通り）で②の手順を各10,000回ずつ繰り返します．有意水準はp=0.05とします．

αエラーの結果

　

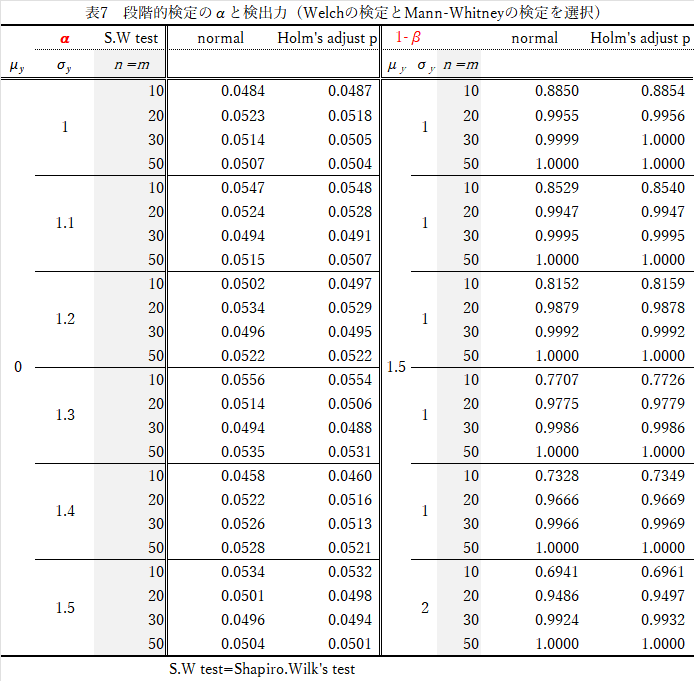
結果（表7）の要約

• $\alpha$について
  • $Shapiro-Wilk$の検定で，$Holm$修正しても，しなくてもほぼ差なし．
  • $n$の大きさを変えても大差なし．
• 検出力（1-$\beta$）
  • $Shapiro-Wilk$の検定で，$Holm$修正した方が，わずかに検出力は高い．
  • $n$が大きいほど検出力は高い．
• $Levene$の検定の有意水準を変えても大差なし（やや検出力が上がる）
• 等分散性の検定を経過する方法と比べて，遜色ない．

検出力（1-β）の結果

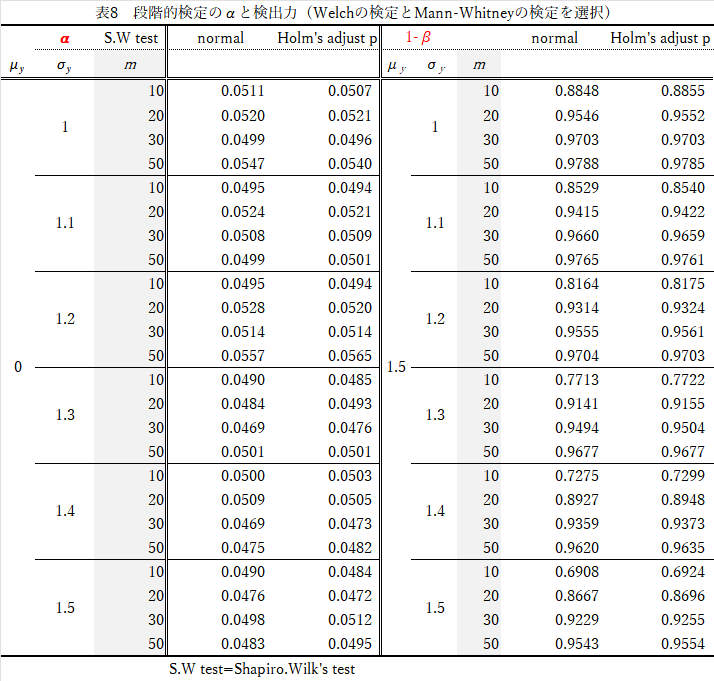
結果（表8）の要約

• $\alpha$について
  • $Shapiro-Wilk$の検定で，$Holm$修正しても，しなくてもほぼ差なし．
  • $n$の大きさを変えても大差なし．
  • $X，Y$の$\sigma$の比が異なると，検出力は下がる．
• 検出力（1-$\beta$）
  • $n$が大きいほど検出力は高い．
  • $X，Y$の$\sigma$の比が異なると，検出力は下がる．
• 等分散性の検定を経過する方法と比べて，やや検出力は高い．

結論

　本シミュレーションの制限は，乱数が正規分布に従う標本に限る，ことです．よって，正規分布以外でも確認する必要はあります．それは後日行うとして，ここまでの結論を述べます．

• 等分散性は確認した方が良い．
  • ただし，2標本$t$検定，$Welch$の検定，$Mann-Whitney$の検定を使い分けるのであれば，です．
  • なぜなら，2標本$t$検定，$Mann-Whitney$の検定は不等分散のとき，検出力が低くなるから．
• 正規分布に従うか否かは確認した方が良い（判定保留）．
  • $Mann-Whitney$の検定では検出力が低くなるから
  • 正規乱数しか使っていないので，2標本$t$検定，$Welch$の検定の挙動は不明，ゆえに判定保留です．
• $Welch$の検定，$Mann-Whitney$の検定を使い分ける段階的検定でも，ほぼ違いはない．
  • 2標本t検定にこだわる必要はなさそうです．しかし，2標本t検定を否定するものではありません．
• 標本が正規分布に従うことが明らかであれば，$Welch$の検定を適用するだけでも問題はない．

　しかし，やはりこれも理論上の話ですので，現実がそれに従うとは限らない点に注意が必要です．

追記

　これも解決しようと思いますが、段階的検定がダメというなら、多変量解析の前に差の検定や相関、分割表の検定を行うのも無しですよね。
　ステップワイズ法はp値を見ながら説明変数を決めるのでダメと言いますよね。理論計算で勝手に選んでるのに？
　矛盾は沢山ありますが、迷える子羊を悩ましてるのは、迷える子羊そのものだと思います。

　

1. 「間違いをわきまえたうえで」と書くと誤解を受けますが，正解がわからない以上，間違いである可能性はあります．明らかな間違いで，より最適な方法が提案されているのであればそちらを選択すべきです．しかし，最適な方法が正解とは限りません． ↩