Introduction to Heuristics Contestの延長戦1位解法解説

はじめに

最近会社の合宿でIntroduction to Heuristics Contestの問題を使って演習しました。
合宿の準備をしていたら延長戦1位がとれたので、せっかくなので記事を書くことにしました。
一部tatyamさんを始めとしたいろいろな人に協力を仰いだので、とても感謝です。特に、ハンガリアン法に用いる辺の重みのつけ方はtatyamさんに直接教えてもらってたいへん助かりました。
ちなみに僕は先人の強い解法を組み合わせただけなので、僕自身のすごいポイントはあんまりないです。
あと、初心者の人はこの記事を読むより公式解説を読んだ方が無限倍学びがあると思います。

順位表

1位です。

提出コード
https://atcoder.jp/contests/intro-heuristics/submissions/55840081

問題概要

365日間、26種類のコンテストから1日あたり1個ずつ開催し、ユーザーの満足度をなるべく上げることが目的です。

満足度は0からスタートし、コンテストの開催状況によって変化します。
変化させる要素は大きく分けて2種類あります。
変化要素1つ目は、コンテストを開催することで満足度が増加することです。
具体的には$d$日目にコンテスト$i$が開催された場合、満足度$s_{d,i}$が予めわかっています。

変化要素2つ目は、コンテストを開催しない間、満足度が下がり続けることです。

コンテストごとに満足度の下がりやすさ$C_i$が与えられます。
各日付において、$コンテストiが前回開催されてから経過した日数\times C_i$ だけ満足度が下がります。
例えば、$C_i=10$でDay3, Day7にコンテスト$i$が開催された場合のDay8までの満足度の低下量は以下のようになります。

\displaylines{
C_1によるDay8までの満足度低下量 & = &10\times (1+2+1+2+3+1) \\
& = & 100
}

このように、コンテストを開催することによる満足度の増加と、コンテストを開催しないことによる満足度の低下を365日間26コンテストについて合計し、$10^6$を足したものが最終的な満足度になります。

この問題は公式解説が親切なことで有名なヒューリスティック問題です。AHCに興味ある全人類やりましょう。

解法概要

1. 高速で質のいい初期解をつくる
2. 質のいい近傍の焼きなまし

これだけです。
なぜか「高速で質のいい初期解をつくる」だけができている提出コードと「高速で質のいい近傍の焼きなまし」だけできている提出コードを独立に見つけたので、合体させました。

高速で質のいい初期解をつくる

tatyamさんの解説の通りやるだけです。
とはいえ、僕の理解力だと理解が大変だったので補足します。

まず、問題を簡単にします。

1. 365日間の満足度ではなく、20日間の満足度の増加量を最大化することを考える
2. 20日間の中で、同じコンテストは1回しか開催しない

問題文の再掲ですが、1日の中でコンテストは1つしか開催しません。

ここで、日付dにコンテストiが開催された場合の満足度の増加量が計算できれば
「26個の頂点集合(コンテスト)と20個の頂点集合(日付)で構成される2部グラフから、最大重み最大マッチングを求める問題」と言い換えることができます。（満足度の増加量については少し後で説明します。）

最大重み最大マッチングとはなにかというと、
どの各点も2辺以上つながらず、(マッチング)
辺の数が最大になり、（最大マッチング）
重みの合計が最大である部分グラフ（最大重みマッチング）
のことです。

今回簡単にした問題で表すと、
同じ日付に複数のコンテストが開催されず、同じコンテストが複数の日付に開催されない。（マッチング）
全ての日付でコンテストが開催される（最大マッチング）
満足度の増加量の合計が最大になる（最大重みマッチング）
となります。

最大重み最大マッチングを解く方法はいくつかあるようですが、今回はハンガリアン法を使いました。
以下のコードの配列weights_とそのサイズN,Mを問題に合わせて設定すれば、そのまま使えます。
アルゴリズム橙や赤の複数名に聞いたんですが、ハンガリアン法は中身を理解しなくても使い方さえ知ってればいいとのことでした。僕も中身を理解するのを諦めました。

hungarian.cpp

// ここだけ自分で変える
constexpr int N = W;  // ハンガリアン法で少ない法の集合の頂点数。今回は対象期間の日数
constexpr int M = CN; // ハンガリアン法で多い法の集合の頂点数。今回はコンテスト数

// input : N * M cost matrix (bipatite graph)
// output : {cost, matching} size-N matching with minimum cost
// constraint : N <= M, time : O(N^2 M)
int weights_[N][M];
vector<int> hungarian()
{
    constexpr int n = N + 1, m = M + 1;
    assert(n <= m);
    vector<int> u(n), v(m), p(m), ans(n - 1);
    for (int i = 1; i < n; i++)
    {
        p[0] = i;
        int j0 = 0; // add "dummy" worker 0
        vector<int> dist(m, INT_MAX), pre(m, -1);
        vector<bool> done(m + 1);
        do
        { // dijkstra
            done[j0] = true;
            int i0 = p[j0], j1, delta = INT_MAX;
            for (int j = 1; j < m; j++)
                if (!done[j])
                {
                    int cur = weights_[i0 - 1][j - 1] - u[i0] - v[j];
                    if (cur < dist[j])
                        dist[j] = cur, pre[j] = j0;
                    if (dist[j] < delta)
                        delta = dist[j], j1 = j;
                }
            for (int j = 0; j < m; j++)
            {
                if (done[j])
                    u[p[j]] += delta, v[j] -= delta;
                else
                    dist[j] -= delta;
            }
            j0 = j1;
        } while (p[j0]);
        while (j0)
        { // update alternating path
            int j1 = pre[j0];
            p[j0] = p[j1], j0 = j1;
        }
    }
    for (int j = 1; j < m; j++)
        if (p[j])
            ans[p[j] - 1] = j - 1;
    return ans; // min cost
}

さて、本来は365日間のコンテストスケジュールを計画する問題です。
最初の20日の満足度増加量を高くすることを考えましたが、20日間の解から1日目のコンテストだけ確定させ、2日目から21日目までの20日間で再度最大重み最大マッチング問題を解いて2日目のコンテストだけ確定、2日目を繰り返し…、を繰り返せば365日間のスケジュールを計画できます。
このように、短い期間で解いた解の一部を固定、少しずらした期間の解を出してまた固定、を繰り返す手法をローリングホライズンと呼びます。

さて、先ほど省いた、日付dにコンテストiが開催された場合の満足度の増加量を計算する部分について説明します。

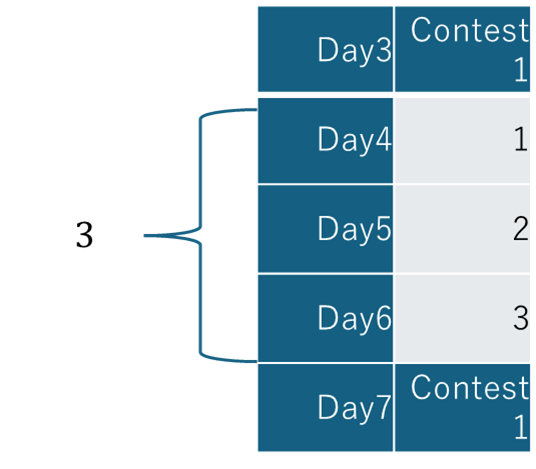
まず、ある1つのコンテストが2回開催されるときの開催されていない期間の満足度の下がりやすさは以下のような形をしています。

$1+2+3+...+n$

これは初項1、交差1の等差数列の和として表現できるので、以下の式で計算できます。

$\sum_{k=1}^{n} n= \frac{n(n+1)}{2}$

以下のように3日空いている場合、$\frac{3(3+1)}{2}=6$が満足度低下の係数となります。

さて、今回考える問題では各コンテストは20日の間で1回しか開催しないことにしたので、20日後時点の満足度を考える場合、過去に開催された1回分と、今回追加予定の1回分だけを考慮すればいいです。
対象の20日間のw日目にコンテストを開催する場合の満足度の低下係数の低下量を考えると、満足度の増加に寄与する係数が求められます。

\displaylines{
係数の低下量 & = & 元の満足度低下係数-w日目に開催した場合の満足度低下係数 \\
& = &\frac{(e+f)(e+f+1)}{2}-\Biggl(  \frac{e(e+1)}{2}+\frac{f(f+1)}{2} \Biggr) \\
& = & ef
}

$e,f$は各コンテストが最後に開催されてからの経過日数$l$をローリングホライズンの途中で記録しておけば、図のように$w$のみを変数として表現可能です。

$対象期間w日目の満足度の低下係数の増加量=元の満足度低下係数-(w日目までの満足度低下係数+w日目から20日目までの満足度低下)$

満足度の低下係数の低下量が計算できれば、あとはw日目に対応する$s$と$c$から、コンテストiを開催した場合の満足度の増加量が計算できます。$shifted$はローリングホライズンで何日ずらしたかを示します。

$s_{shifted+w,i}+c_i\times e \times f$

20日×26コンテストについての満足度の増加量を全て計算すれば、前述のハンガリアン法が適用できます。

質のいい近傍の焼きなまし

さて、初期解ができたので焼きなましていきたいですね。
焼きなますには近傍を考える必要がありますが、すぐ思いつくのは「$d$日目に開催するコンテストを異なるコンテストに変更する」や「$d$日目に開催するコンテストと$e$日目に開催するコンテストを入れ替える」などでしょうか。

これらのシンプルな近傍では、1回の遷移で解が大きく変わらないため、局所最適解から抜け出すことが難しいです。そのため、近傍を大きくするほど現在の解より優れた解が近傍に含まれる可能性が高くなります。

まず、1つのコンテストだけで見れば、ある日付の開催予定を別の日付にずらすことで改善するかどうかはすぐに確認できます。
ずらす日付候補は元の開催予定日は、他の開催日をまたいてずらすと無駄が多いため、1つ前の開催日から1つ後の開催日までの間とします。

この方法は1つのコンテストの改善具合は簡単に計算できますが、ずらし先の日付は必ず他のコンテストが開催されています。

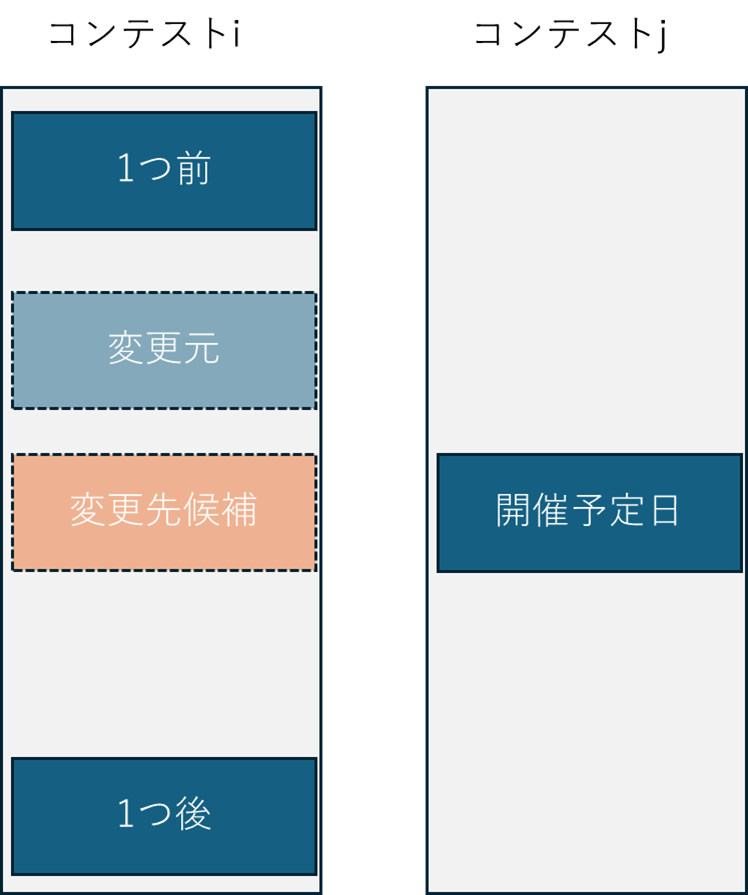
そのため、ずらし先の日付で開催予定のコンテストを同様の仕組みでずらします。
これを繰り返し、最初にずらし始めたコンテストの元の開催日にたどりつけば、すべての日付にコンテストが開催されることを保証できます。
このように、大きな近傍を考える手法を大近傍法と呼びます。

ここで、複数のコンテストの開催日をやみくもにずらすと解がくずれすぎてしまい、改善方向にむかいにくくなります。
そこで、近傍をつくる途中段階で、探索すべき近傍がつくれそうかどうかを判断することを考えます。

まず、焼きなまし法での評価関数の打ち切りを利用します。
最大化問題における通常の遷移条件は以下のように表されます
if (exp(diff / T) >= random_value)
diffは今確認しようとしている近傍解でどの程度スコアが改善されるかを表します。
これを以下のように変形します
if (diff - T * log(random_value) >=0 )
ここで、
- T * log(random_value)の部分は遷移と関係ないのであらかじめ計算してaddとして定義しておきます。
if (diff +add >= 0)

先ほど考えた近傍に、同じコンテストは多くとも1回までしかずらさないというルールを加えます。
そうすると、各開催日をずらすことによるスコアの増加量の計算が、他の計算の邪魔をしなくなります。（同じコンテストが2つ以上ずれた場合、計算対象の日付から前の開催日や後の開催日がずれる可能性があるため）
そうすると、
近傍全体のスコア改善度は以下のように計算できます。
$コンテスト_i の改善度+コンテスト_jの改善度+ \cdots $

大近傍の途中段階では問題制約を満たしていない「ずる」をして改善しやすい状態なので、途中の解で改善度がよくなりそうにならないなら、大近傍を完全につくりきる必要はありません。

先ほど変形した遷移式に合わせ、$コンテスト_i の改善度+ add >=0$を満たすなら次のコンテストをずらして$コンテスト_i の改善度+コンテスト_j の改善度+ add >=0$を満たすならまた次のコンテストをずらし、、と繰り返し、最初の開催日に戻ることができれば近傍解として、解を遷移させることにします。
完成した近傍解は必ず遷移するに値する解ですし、遷移するに値しない解ならすぐ諦めるので、高速に質のいい近傍をつくれます。

さて、ここまででも十分にいい近傍設計と言えますが、一点問題があります。
各コンテストの開催日をずらしだけでは、各コンテストの開催回数は常に一定です。満足度のさがりやすいコンテストは多く開催したほうがいいし、満足度の下がりにくいコンテストは少ない開催数でいいはずなので、コンテストの回数もずらしながら探索できたほうがよりよい解が見つけられそうです。

そこで、ある日付にコンテストを挿入することを考えます。
この場合、さきほどの開催日をずらす方針同様、必ず開催日が重複するコンテストがあります。
このコンテストをずらし、また被ったコンテストが出て、と繰り返しますが、被ったコンテストを削除して終了すれば、1日あたりのコンテストが1種類のみで制約を満たした近傍となります。
先ほどと違い、コンテストごとの開催回数がずれようになり、より多様な解にたどりつくようになります。
なお、挿入操作は影響力が大きすぎるため、大近傍をつくる途中のスコアには重みをつけて小さくして加算し、削除時に本来のスコアで計算しなおします。

試してないこととか気になったこととか

• tatyamさんのコードでは365回ハンガリアン法をやっていたけど、最後の20日ぶんは1回で済むような気がする
• ハンガリアン法で初期解を出すとき、満足度の下がりやすさの分布に応じて1回で考える日数を変えてもいい気がする。今、20日間で考えるということは、開催しない6個のコンテストを選ぶことと言い換えられるため、$26-極端に満足度が下がりにくいコンテスト数$日間に動的に設定するといい気がする
• 最大重み最大マッチングを高速に解くならKuhn-Munkresアルゴリズムとやらがいいという噂を聞いたので、使ってもいいのかも。でもたぶんここ速くしてもこの問題ではそんなに変わらなそう
• omiさんの提出は2020年でコンパイラも今より古い気がするので、コンパイラの優秀さで差がついた可能性は否めないかも
• 提出した1位コードは温度スケジュールを線形にする実験をしたときのままだった。指数的に下げる方もためしたが、スコアが下がった。指数的に下げた方が直観に合うので謎

        // 線形に温度を下げる
        double temp = start_temp + (end_temp - start_temp) * elapsed_rate;
        // 指数的に温度を下げる
        // double temp = powf(start_temp, 1.0 - elapsed_rate) * powf(end_temp, elapsed_rate);

参考