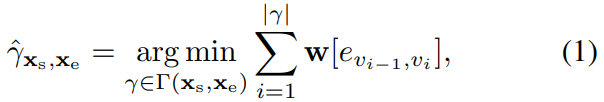論文について
Progressive Minimal Path Method with Embedded CNN
Wei Liao, CVPR, 2022
概要
管状構造のセグメンテーションにおいて、最小経路法にCNNを組み込んだPath-CNNを提案し、中心線とセグメンテーションマスクを生成。
管状構造のセグメンテーションにおいて有望な手法であることがU-Netと比較して示された。
Related Work
Image futures
最小経路法では、画像ヘッシアンをはじめとして人力で調整された特徴を用いて管状構造を識別するが、このような特徴は比較的弱い。
Minimal path computation
最小経路の計算において、誤った経路(short cuts)を得てしまう問題に対して、線幅や向きのような更なる特徴を表現して解決しようと、さまざまな手法が存在している。が、計算コストが飛躍的に増加してしまう。
Methods for road extraction
U-Netのような従来手法を用いて道路抽出を行う場合、大量のアノテーションデータや高いハードウェア要件が必要。
これに対して提案手法であるPath-CNNは
- 経路に基づいた動的な特徴を利用でき、強力な分類が可能
- ダイクストラアルゴリズムと上の動的特徴を組み合わせて、計算効率と精度を両立
- 少ないアノテーションで十分であり、モデル訓練においても2GBのGPUしか使用しない。また、都市や郊外以外の環境・河川にも適用でき、中心線のアノテーションのみで2値セグメンテーションを実現できる
Minimal Path Framework
画像$I$からグラフ$G$が得られるとし、頂点(ピクセル群)$V$, 辺$E$を用いて$G = (V, E)$で表現する。各エッジ$e$には画像特徴に基づく重みが割り当てられるので、これを用いて与えられる始点終点間の最短経路$\hat{\gamma}$を計算する。
最短経路はダイクストラ法の拡張で行う。
基本的にはダイクストラ法と同じだが、確定頂点集合$Q$に追加された頂点$u$について、その隣接頂点$v$との辺の重み$w[e_{u,v}]$をAdaptWeight関数を用いて動的に更新する。更新後に、距離の比較を行い、$d[v] > d[u] + w[e_{u, v}]$であれば$d[v]$を更新し、辿れるように$v$の接続元頂点を$u$とする。
重みの初期値は管状性指標$V$, 辺のユークリッド長$L(e)$, 滑らかさを制御する重み付け係数$\lambda$を用いて、以下で与えられる。

AdaptWeight関数
標準のダイクストラでは辺の重みは固定だが、拡張版では動的に調整する。
- 頂点uから$\pi$によって遡って得られる長さ$L_0$の局所経路$\gamma_L$を求める
- $\gamma_L$を中心線とする一定の幅を持つパッチ$P$を画像$I$から抽出する
- パッチ$P$から回転や曲率の影響を取り除くように補正したパッチ$P_{rect}$を得る
- CNNを分類器として使用し、$P_rect$が前景か背景かを分類し、背景であれば辺重みにペナルティを課す
※疑問点
-
$u$の隣接頂点$v$について、$u$まで伸びる局所経路$\gamma_L$を毎回求めるのが有効なのか分からない。
$u$と$\pi$で一意に決まるので、$v$のループ内で求める必要は無いように思える。
その通り -
$\gamma_L$は$v$を通らない場合もあるはずだが、その分類結果が何故$v$への辺重みを決定しているのが謎である。
→ $u$が管状構造に含まれない場合、そこから伸びる辺$e_{u,v}$によって中心線が構成されることは望ましくない。ほかに$v$を低コストで含むような良い経路があるはずなので、高いコストでペナルティを課す。
Path-CNN Method
Short cutsの分類
- Type 1:
正しい経路が非常に長く曲がる場合、背景を横切る場合でもコストが低くなり、誤った経路を選択する - Type 2:
背景が前景に良く似ている場合に背景を通るショートカットが発生する
経路分類
ショートカットを回避するためにダイクストラを拡張(Algorithm 2によって)し、背景にあたる辺の重みにペナルティを課し、経路選択を抑制する
トレーニング
中心線のみをアノテーションとして使用し、中心線に沿った補正済みパッチを前景としてCNNをトレーニング。
推論
ダイクストラアルゴリズム内のAdaptWeight関数内において局所経路を求め、切り出したパッチをCNNに入力することで推論する
最小経路法とCNNの相互作用
CNNによる動的な特徴学習によって、局所経路の分類制度が向上し、ショートカットのType1, Type2を統一的に回避できる
最小経路法によって、トポロジーが保証され、経路が接続された形状を維持できる。複雑な形状でも分類が容易になる。
実験結果
データセットとして、中心線アノテーションが提供されている4つの衛星画像データセットを使用。
CNNの分類性能と中心線のセグメンテーションの2つについて述べられている。
CNNの分類性能
$11 \times 11$から$71 \times 71$までの解像度範囲で画像をテスト。

中心線によってパッチを補正することによって、分類制度が大幅に向上した。
中心線セグメンテーション
指標として、真の中心線との平均距離を以下で定義して誤差を評価。
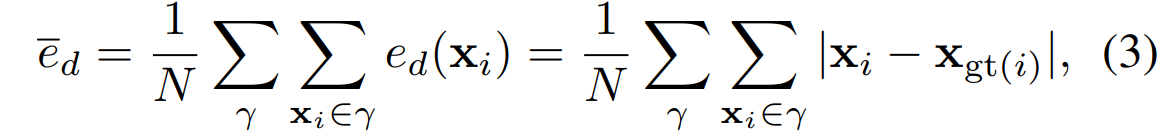
Path-CNNは全てのデータセットで他手法を上回る精度を達成。

真の中心線との誤差分布をみても、視覚的に良くなっていると判断できる

U-Netとの比較
- 中心線アノテーションを用いたU-Net
- マスクアノテーションを用いたU-Net
- Path-CNN
の3つでマスクセグメンテーションの精度(Dice)を比較。Path-CNNがDiceで2倍以上のスコアを記録。

U-Netで得られる推論マスク。真のアノテーションとはかけ離れている。

Path-CNNによって得られる推論マスク(c)は、真のアノテーションに近いマスクを得られている。

まとめ
CNNは手動で調整された画像特徴を強化、最小経路法は幾何的な事前情報によってCNNの性能を向上させるとともに、中心線のトポロジーを保証する。
経路に沿ったパッチをCNNで分類することによって、2種類の誤った経路選択を回避し、複雑な形状を持つ場合や困難な環境においてより正確な中心線セグメンテーションが可能。